Слайд 2Базы данных
Функциональные зависимости
Лекция 7
Пусть задана переменная отношения R, и X и Y

являются произвольными подмножествами заголовка R («составными» атрибутами).
В значении переменной отношения R атрибут Y функционально зависит от атрибута X в том и только в том случае, если каждому значению X соответствует в точности одно значение Y. В этом случае говорят также, что атрибут X функционально определяет атрибут Y (X является детерминантом (определителем) для Y, а Y является зависимым от X).
Будем обозначать это как R.X→R.Y.
Слайд 3Базы данных
Функциональные зависимости
Лекция 7
Для примера будем использовать отношение СЛУЖАЩИЕ_ПРОЕКТЫ {СЛУ_НОМ, СЛУ_ИМЯ, СЛУ_ЗАРП,

ПРО_НОМ, ПРОЕКТ_РУК}. Очевидно, что если СЛУ_НОМ является первичным ключом отношения СЛУЖАЩИЕ, то для этого отношения справедлива функциональная зависимость (Functional Dependency – FD) СЛУ_НОМ→СЛУ_ИМЯ.
Слайд 4Базы данных
Функциональные зависимости
Лекция 7
Для тела отношения СЛУЖАЩИЕ_ПРОЕКТЫ выполняются следующие FD:
СЛУ_НОМ→СЛУ_ИМЯ
СЛУ_НОМ→СЛУ_ЗАРП
СЛУ_НОМ→ПРО_НОМ
СЛУ_НОМ→ПРОЕКТ_РУК
{СЛУ_НОМ, СЛУ_ИМЯ}→СЛУ_ЗАРП
{СЛУ_НОМ, СЛУ_ИМЯ}→ПРО_НОМ
{СЛУ_НОМ,

СЛУ_ИМЯ}→{СЛУ_ЗАРП, ПРО_НОМ}
ПРО_НОМ→ПРОЕКТ_РУК
и т. д.
Эти FD должны быть верны для любого допустимого значения переменной отношения СЛУЖАЩИЕ_ПРОЕКТЫ и могут рассматриваться как инварианты, или ограничения целостности этой переменной отношения.
Слайд 5Базы данных
Функциональные зависимости
Лекция 7
Поскольку имена всех служащих различны, то выполняются и такие

FD :
СЛУ_ИМЯ→СЛУ_НОМ
СЛУ_ИМЯ→СЛУ_ЗАРП
СЛУ_ИМЯ→ПРО_НОМ
и т. д.
Т. к. никакие двое служащих, участвующие в разных проектах, не получают одинаковую зарплату, выполняется FD:
СЛУ_ЗАРП→ПРО_НОМ
Если атрибут A отношения R является возможным ключом, то для любого атрибута B этого отношения всегда выполняется FD A→B.
Слайд 6Базы данных
Функциональные зависимости
Лекция 7
FD A→B называется тривиальной, если A⊇B (т. е. множество

атрибутов A включает множество B или совпадает с множеством B).
Любая тривиальная FD всегда выполняется. Например, в отношении СЛУЖАЩИЕ_ПРОЕКТЫ всегда выполняется FD
{СЛУ_ЗАРП, ПРО_НОМ}→СЛУ_ЗАРП
Тривиальные FD нельзя трактовать как ограничения целостности.
Слайд 7Базы данных
Замыкание множества функциональных зависимостей
Лекция 7
Замыканием множества FD S является множество FD

S+, включающее все FD, логически выводимые из FD множества S.
Два примера FD, из которых следуют (или выводятся) другие FD:
Для отношения СЛУЖАЩИЕ_ПРОЕКТЫ выполняется, например, FD СЛУ_НОМ→СЛУ_ЗАРП, ОТД_НОМ}. Из этой FD выводятся FD СЛУ_НОМ→СЛУ_ЗАРП и СЛУ_НОМ→ОТД_НОМ.
Имеется также пара FD СЛУ_НОМ→ОТД_НОМ и ОТД_НОМ→ПРОЕКТ_РУК. Из них выводится FD СЛУ_НОМ→ПРОЕКТ_РУК.
FD вида СЛУ_НОМ→ПРОЕКТ_РУК называются транзитивными, поскольку ПРОЕКТ_РУК зависит от СЛУ_НОМ «транзитивно», через ПРО_НОМ.
FD A→C называется транзитивной, если существует такой атрибут B, что имеются функциональные зависимости A→B и B→C и отсутствует функциональная зависимость C→A.
Слайд 8Базы данных
Аксиомы Армстронга
Лекция 7
Пусть A, B и C являются (в общем случае,

составными) атрибутами отношения R. Множества A, B и C могут иметь непустое пересечение. Для краткости будем обозначать через AB A UNION B. Тогда:
если B ⊆A, то A→B (рефлексивность);
если A→B, то AC→BC (пополнение);
если A→B и B→C, то A→C (транзитивность).
Слайд 9Базы данных
Аксиомы Армстронга
Лекция 7
Дейт по практическим соображениям предложил расширить базовый набор правил

вывода еще пятью правилами:
A→A (самодетерминированность);
если A→BC, то A→B и A→C (декомпозиция);
если A→B и A→C, то A→BC (объединение);
если A→B и C→D, то AC→BD (композиция);
если A→BC и B→D, то A→BCD (накопление) .
Слайд 10Базы данных
Замыкание множества атрибутов
Лекция 7
Пусть заданы отношение R, множество Z атрибутов этого

отношения (подмножество заголовка R, или составной атрибут R) и некоторое множество FD S, выполняемых для R. Тогда замыканием Z над S называется наибольшее множество Z+ таких атрибутов Y отношения R,
что FD Z→Y входит в S+.
Суперключом отношения R называется любое подмножество K заголовка R, включающее, по меньшей мере, хотя бы один возможный ключ R.
Одно из следствий этого определения состоит в том, что подмножество K заголовка отношения R является суперключом тогда и только тогда, когда для любого атрибута A (возможно, составного) заголовка отношения R выполняется FD K→A. В терминах замыкания множества атрибутов K является суперключом тогда и только тогда, когда K+ совпадает с заголовком R.
Слайд 11Базы данных
Минимальное покрытие множества FD
Лекция 7
Множество FD S2 называется покрытием множества FD

S1, если любая FD, выводимая из S1, выводится также из S2.
S2 является покрытием S1 тогда и только тогда, когда S1+⊆S2+. Два множества FD S1 и S2 называются эквивалентными, если каждое из них является покрытием другого, т. е. S1+ = S2+.
Множество FD S называется минимальным в том и только в том случае, когда удовлетворяет следующим свойствам:
правая часть любой FD из S является множеством из одного атрибута (простым атрибутом);
детерминант каждой FD из S обладает свойством минимальности; это означает, что удаление любого атрибута из детерминанта приводит к изменению замыкания S+, т. е. порождению множества FD, не эквивалентного S;
удаление любой FD из S приводит к изменению S+, т. е. порождению множества FD, не эквивалентного S.
Слайд 12Базы данных
Декомпозиция без потерь и FD
Лекция 7
Считаются правильными такие декомпозиции отношения, которые

обратимы, т. е. имеется возможность собрать исходное отношение из декомпозированных отношений без потери информации.
Такие декомпозиции называются декомпозициями без потерь.
Слайд 13Базы данных
Корректные и некорректные декомпозиции отношений
Лекция 7
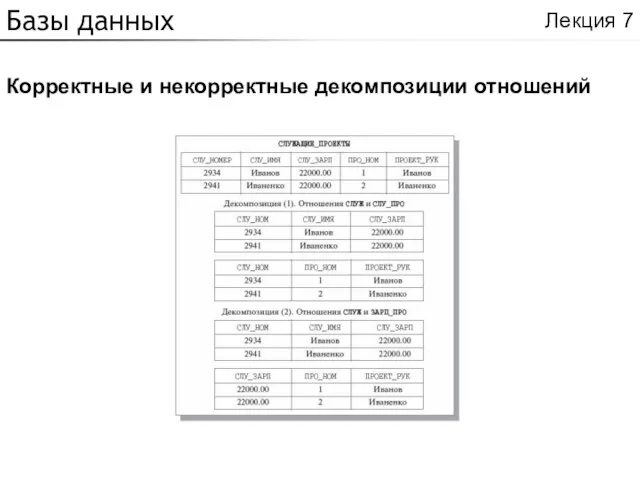
Слайд 14Базы данных
Теорема Хита
Лекция 7
Пусть задано отношение r {A, B, C} (A, B

и C, в общем случае, являются составными атрибутами) и выполняется FD A→B.
Тогда r = (r PROJECT{A, B}) NATURAL JOIN (r PROJECT{A, C}).
Слайд 15Базы данных
Минимальные FD
Лекция 7
Атрибут B минимально зависит от атрибута A, если выполняется

минимальная слева FD A→B.
Минимальной слева называется FD с минимальным детерминантом.
Например, в отношении СЛУЖАЩИЕ_ПРОЕКТЫ выполняются FD СЛУ_НОМ→СЛУ_ЗАРП и {СЛУ_НОМ, СЛУ_ИМЯ}→СЛУ_ЗАРП. Первая FD является минимальной слева, а вторая — нет.
Поэтому СЛУ_ЗАРП минимально зависит от СЛУ_НОМ, а для {СЛУ_НОМ, СЛУ_ИМЯ} свойство минимальной зависимости не выполняется.














 Презентация на тему Образ черкесского воина в творчестве М.Ю.Лермонтова
Презентация на тему Образ черкесского воина в творчестве М.Ю.Лермонтова Презентация без названия
Презентация без названия Русская механика
Русская механика 85098d15eff741ddb056b49a74c773e6
85098d15eff741ddb056b49a74c773e6 Общественный фонд«Добровольное Общество «Милосердие»проект«Казахстан без Сирот!»
Общественный фонд«Добровольное Общество «Милосердие»проект«Казахстан без Сирот!» Олимпийские игры – символ мира и единения
Олимпийские игры – символ мира и единения Правила личной гигиены
Правила личной гигиены Предложение Группы компаний СИС для ОФИСНЫХ ЗДАНИЙ. - презентация___________________________________________________________________________________________________________________
Предложение Группы компаний СИС для ОФИСНЫХ ЗДАНИЙ. - презентация___________________________________________________________________________________________________________________ Дизайн упаковки. Темы для выпускной квалификационной работы
Дизайн упаковки. Темы для выпускной квалификационной работы Двухфакторная теория Герцберга
Двухфакторная теория Герцберга 20170225_pochvy
20170225_pochvy Компьютер и здоровье 10 класс
Компьютер и здоровье 10 класс Правила санитарии, гигиены и безопасной работы
Правила санитарии, гигиены и безопасной работы Нормативные документы. Обязанности вожатого
Нормативные документы. Обязанности вожатого Презентация на тему Темза
Презентация на тему Темза  «Беспроводные системы связи в управлении перевозочным процессом и обеспечении безопасности движения»
«Беспроводные системы связи в управлении перевозочным процессом и обеспечении безопасности движения» Презентация на тему Как вести себя дома
Презентация на тему Как вести себя дома  Криминогенные ситуации в доме, в подъезде, на улице (5 класс)
Криминогенные ситуации в доме, в подъезде, на улице (5 класс) Древние орнаменты в творчестве художников разного времени. 6 класс
Древние орнаменты в творчестве художников разного времени. 6 класс Внедрение принципов экологического менеджмента в пао ФСК ЕЭС
Внедрение принципов экологического менеджмента в пао ФСК ЕЭС Югендстиль. Возникновение и описание
Югендстиль. Возникновение и описание Хит 2009 Экзотический фрукт!
Хит 2009 Экзотический фрукт! С чего начать свое дело: бизнес-план (пошаговая инструкция: как составить бизнес-план)
С чего начать свое дело: бизнес-план (пошаговая инструкция: как составить бизнес-план) Обучение иноязычному дискурсу с применением компьютерных технологий. Темы работ
Обучение иноязычному дискурсу с применением компьютерных технологий. Темы работ Представление курса
Представление курса Зеленый материк планеты
Зеленый материк планеты ПРОЕКТЫ СТАНДАРТОВ В СИСТЕМЕ ПЕРСОНАЛЬНОГО УЧЕТА НАСЕЛЕНИЯ РОССИИ Е. В. Бойченко ЗАО «ИВЦ ИНСОФТ»
ПРОЕКТЫ СТАНДАРТОВ В СИСТЕМЕ ПЕРСОНАЛЬНОГО УЧЕТА НАСЕЛЕНИЯ РОССИИ Е. В. Бойченко ЗАО «ИВЦ ИНСОФТ» Формы отчета о самообследовании
Формы отчета о самообследовании