Исследование формообразования при фрезоточении многогранных профильных поверхностей

Объект исследования:
https://youtu.be/ykB6VsFC_cA
Предмет исследования:

Задачи исследования:
Проработать методы графического и аналитического описания процесса полигонального фрезоточения
Рассмотреть применение различных типов фрез для указанных способов обработки
Исследовать возможность фрезоточения многогранников с полными и неполными гранями
Изучить существующие способы обработки многогранных (полигональных) поверхностей фрезоточением

Схема графического моделирования фрезоточения идеального многогранника:

Схема графического моделирования фрезоточения многогранника с неполными гранями

Расчетная схема фрезоточения обощенного многогранника

Угол между вершинами многогранника:
ϕ = 2π/n,
где n – число граней фрезеруемой детали.
S/2 = D⋅cos(π/n)/2,
где S – размер "под ключ",
D – диаметр описанной окружности детали.
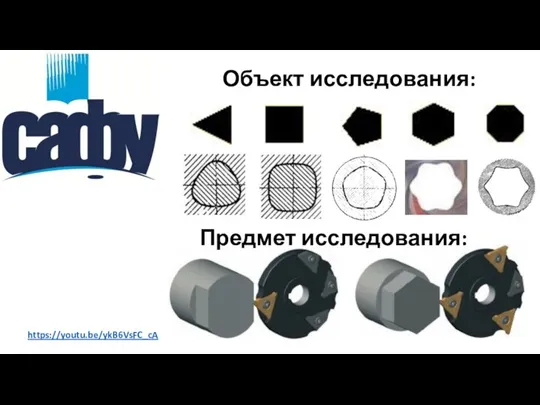
Расчет погрешности формообразования
Диаметр второго (по размеру и положению – вдоль обрабатываемой грани) зуба фрезы:
dФ2 = 2[((D + dФ1)/2)⋅cos(π(z – 2)/(nz) – (D/2)⋅cos(π/n))],
где z – число зубьев фрезы,
dФ1 – диаметр первого (по размеру и положению – вдоль обрабатываемой грани) зуба фрезы, начального при проектировании.
Аналогично для последующих зубьев фрезы:
dФ3 = 2[((D + dФ1)/2)⋅cos(π(z – 4)/(nz) – (D/2)⋅cos(π/n))],
dФ4 = 2[((D + dФ1)/2)⋅cos(π(z – 6)/(nz) – (D/2)⋅cos(π/n))], и т.д.
Для зуба максимального диаметра:
dФmax = D(1 – cos(π/n)) + dФ1.
Погрешность обработки – величина "гребешка" (рис. 3):
δ = dФmax – В,
В = [d2Фmax – к2]0,5,
к = к2 – (D – dФmax)tg(ϕ/z),
к2 = dФ2⋅sinψ2 = dФ2⋅sin[ϕ((z – 2)/2z) + arccos((d2Ф2) + (D + dФ1)2)/(2(D + dФ1) dФ2)].

Выводы:
Рассмотрен и проанализирован вариант внешнего полигонального фрезоточения для поверхности с произвольным числом плоских граней (схема встречного фрезерования)
Разработан графический метод формообразования полигональным фрезоточением плоских многогранников
Исследовано полигональное фрезоточение фрезами с постоянной и переменной высотой зуба для полных и неполных плоских многогранников
Получены зависимости погрешности формообразования (высоты остаточной макронеровности) от параметров настройки технологической системы