Содержание
- 2. История арифметических прогрессий В Вавилонском царстве всеми расчетами занимались писцы, которые принадлежали к высшему сословию. Школа,
- 3. История арифметических прогрессий Некоторые формулы, относящиеся к прогрессиям были известны китайским и индийским ученым. Слово «прогрессия»
- 4. ДРЕВНЕЙШАЯ ПРОГРЕССИЯ Древнейшая задача на прогрессии – не вопрос о вознаграждении изобретателя шахмат, насчитывающий за собой
- 5. Решение. Количества хлеба, полученные людьми, составляют возрастающую арифметическую прогрессию. Пусть первый ее член равен Х, а
- 6. Числа Фибоначчи Древняя история богата выдающимися математиками. А вот из математиков средневековья в школьном курсе названо
- 7. Гаусс Карл Фридрих (30.04.1777 - 23.02.1855) Дед Гаусса был бедным крестьянином, отец — садовником, каменщиком, смотрителем
- 8. До самой старости он привык большую часть вычислений производить в уме. Свободно владея множеством языков, Гаусс
- 9. Теория Рамсея и арифметические прогрессии Арифметическая прогрессия — это последовательность чисел, в которой разность между соседними
- 10. Теория Рамсея и арифметические прогрессии Но тогда у нас получится красная арифметическая прогрессия 2,5, 8. Итак,
- 11. Применение арифметических прогрессий Задачи на прогрессии, дошедшие до нас из древности, были связаны с запросами хозяйственной
- 12. Финансовая математика В финансовой математике для решения различных задач главным математическим аппаратом является понятие «процентов» и
- 13. Метрология, стандартизация, сертификация Ряды предпочтительных чисел должны отвечать следующим требованиям: быть бесконечными как в сторону малых,
- 15. Скачать презентацию












 Поколение молодости REV 7-2014
Поколение молодости REV 7-2014 Взаимодействие агентов в многоагентных системах
Взаимодействие агентов в многоагентных системах ФАКТОГРАФИЧЕСКИЕ БАЗЫ ДАННЫХ НАЦИОНАЛЬНОЙ БИБЛИОТЕКИ БЕЛАРУСИ КАК ИСТОЧНИК ИНФОРМАЦИИ О НАЦИОНАЛЬНЫХ ОБЪЕКТАХ Кузьминич Т. Нац
ФАКТОГРАФИЧЕСКИЕ БАЗЫ ДАННЫХ НАЦИОНАЛЬНОЙ БИБЛИОТЕКИ БЕЛАРУСИ КАК ИСТОЧНИК ИНФОРМАЦИИ О НАЦИОНАЛЬНЫХ ОБЪЕКТАХ Кузьминич Т. Нац Филиппова Елена Константиновна – учитель Филиппова Елена Константиновна – учитель русского языка и литературы Квалификационная
Филиппова Елена Константиновна – учитель Филиппова Елена Константиновна – учитель русского языка и литературы Квалификационная Новости недели. Новосибирск
Новости недели. Новосибирск Художники Сенгилеевского района
Художники Сенгилеевского района ПрезентацияРаздел 2.2
ПрезентацияРаздел 2.2 Международные модели управления персоналом
Международные модели управления персоналом Цели внедрения системы бюджетирования
Цели внедрения системы бюджетирования Деление плоскости на четыре части, в зарисовке
Деление плоскости на четыре части, в зарисовке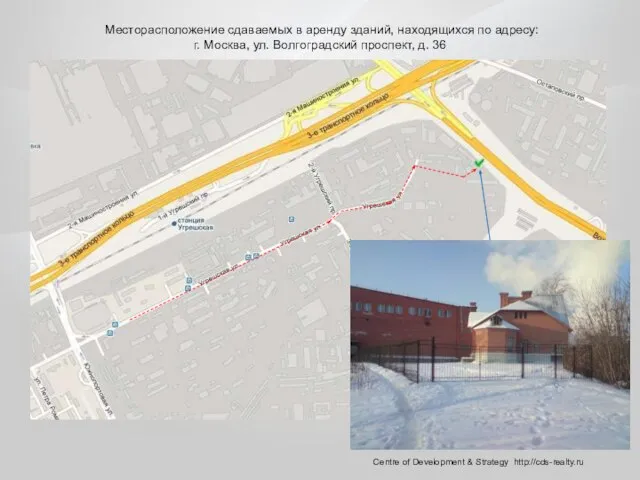 Месторасположение сдаваемых в аренду зданий, находящихся по адресу: г. Москва, ул. Волгоградский проспект, д. 36
Месторасположение сдаваемых в аренду зданий, находящихся по адресу: г. Москва, ул. Волгоградский проспект, д. 36 Филимоновская игрушка. Фотоотчет
Филимоновская игрушка. Фотоотчет Фридрих Шиллер
Фридрих Шиллер Презентация на тему Особые экономические зоны стран мира
Презентация на тему Особые экономические зоны стран мира  Фотоэлектрические модули. (Лекция 5)
Фотоэлектрические модули. (Лекция 5) The Victorian Era 1837 -1901
The Victorian Era 1837 -1901 Династический кризис 1825 г. Выступление декабристов
Династический кризис 1825 г. Выступление декабристов ВЕЛИКАЯ ОТЕЧЕСТВЕННАЯ ВОЙНА СОВЕТСКОГО СОЮЗА.
ВЕЛИКАЯ ОТЕЧЕСТВЕННАЯ ВОЙНА СОВЕТСКОГО СОЮЗА. Электронное взаимодействие между организациями ислужбой занятости населения
Электронное взаимодействие между организациями ислужбой занятости населения Порядок подачи заявления о преступлении
Порядок подачи заявления о преступлении Избушка
Избушка Сказочный мир Шарля Перро
Сказочный мир Шарля Перро ПОП-АРТ
ПОП-АРТ Осенние поделки
Осенние поделки Управление эмоциями
Управление эмоциями КОТЕЛЬНАЯ 4 Х 15 МВт
КОТЕЛЬНАЯ 4 Х 15 МВт Основные этапы разработки ООП
Основные этапы разработки ООП «Свирель серебряного века»
«Свирель серебряного века»