История развития тригонометрии

Слово тригонометрия впервые встречается в 1505 году в заглавии книги немецкого математика Питискуса.
Тригонометрия – слово греческое и в буквальном переводе означает измерение треугольников.
В данном случае измерение треугольников следует понимать как решение треугольников, т.е. определение сторон, углов и других элементов треугольника, если даны некоторые из них. Большое количество практических задач, а также задач планиметрии, стереометрии, астрономии и других приводятся к задаче решения треугольников.
Возникновение тригонометрии связано с землемерием, астрономией и строительным делом.
Вступление

История становления тригонометрии
Хотя название науки возникло сравнительно недавно, многие относимые сейчас к тригонометрии понятия и факты были известны ещё две тысячи лет назад.
Впервые способы решения треугольников, основанные на зависимостях между сторонами и углами треугольника, были найдены древнегреческими астрономами Гиппархом (2 в. до н. э.) и Клавдием Птолемеем (2 в. н. э.). Позднее зависимости между отношениями сторон треугольника и его углами начали называть тригонометрическими функциями.

Значительный вклад в развитие тригонометрии внесли арабские ученые Аль-Батани (850-929) и Абу-ль-Вафа, Мухамед-бен Мухамед (940-998), который составил таблицы синусов и тангенсов через 10’ с точностью до 1/604.
Теорему синусов уже знали индийский ученый Бхаскара (р. 1114, год смерти неизвестен) и азербайджанский астроном и математик Насиреддин Туси Мухамед (1201-1274). Кроме того, Насиреддин Туси в своей работе «Трактат о полном четырехстороннике» изложил плоскую и сферическую тригонометрию как самостоятельную дисциплину.

Долгое время тригонометрия носила чисто геометрический характер, т. е. факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов.
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики.

Аналитическая теория тригонометрических функций в основном была создана выдающимся математиком XVIII веке Леонардом Эйлером (1707-1783) членом Петербургской Академии наук.
Громадное научное наследие Эйлера включает блестящие результаты, относящиеся к математическому анализу, геометрии, теории чисел, механике и другим приложениям математики.
Именно Эйлер первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения.

После Эйлера тригонометрия приобрела форму исчисления: различные факты стали доказываться путем формального применения формул тригонометрии, доказательства стали намного компактнее проще,
Таким образом, тригонометрия, возникшая как наука о решении треугольников, со временем развилась и в науку о тригонометрических функциях.
Позднее часть тригонометрии, которая изучает свойства тригонометрических функций и зависимости между ними, начали называть гониометрией .Термин гониометрия в последнее время практически не употребляется.

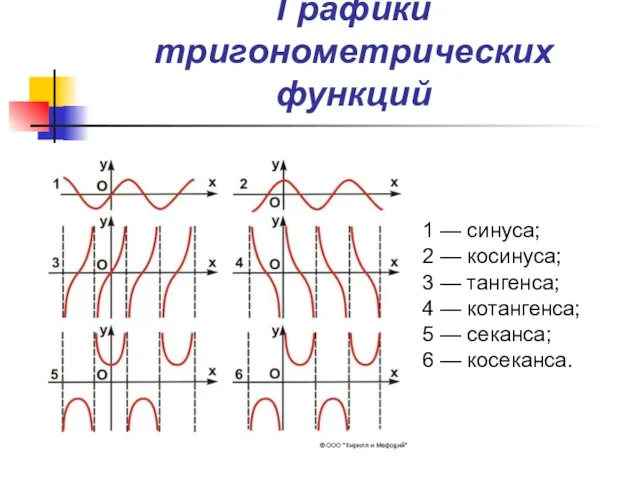
Графики тригонометрических функций
1 — синуса;
2 — косинуса;
3 — тангенса;
4 — котангенса;
5 — секанса;
6 — косеканса.

Синус sin
Длительную историю имеет понятие синус. Фактически различные отношения отрезков треугольника и окружности (а по существу, и тригонометрические функции) встречаются уже в III веке до н.э. в работах великих математиков Древней Греции – Евклида, Архимеда, Апполония Пергского. В римский период эти отношения достаточно систематично исследовались Менелаем (I век н.э.), хотя и не приобрели специального названия. Современный синус, например, изучался как полухорда, на которую опирается центральный угол, или как хорда удвоенной дуги.
В IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Отрезок АМ он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна).

y = sin x,
D(y) = R, E(y) = [-1;1]

Косинус cos
Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”).

y = cos x,
D (y) = R, E(y) = [-1;1]

Тангенс tg
Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе
Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности).

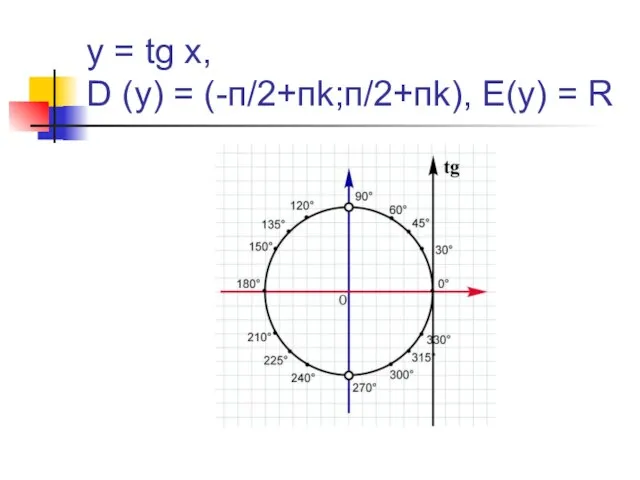
y = tg x,
D (y) = (-п/2+пk;п/2+пk), E(y) = R

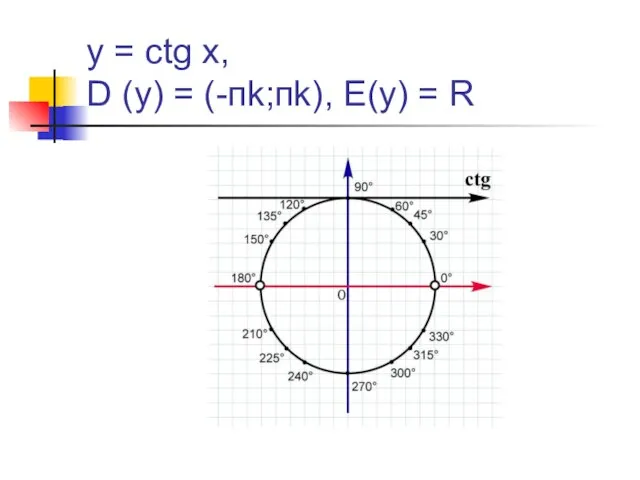
y = ctg x,
D (y) = (-пk;пk), E(y) = R

Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.

Соотношение между тригонометрическими функциями

Формулы двойного угла

Формулы понижения степени

Формулы суммы и разности аргументов

Формулы преобразования произведения в сумму

Формулы преобразования суммы в произведение

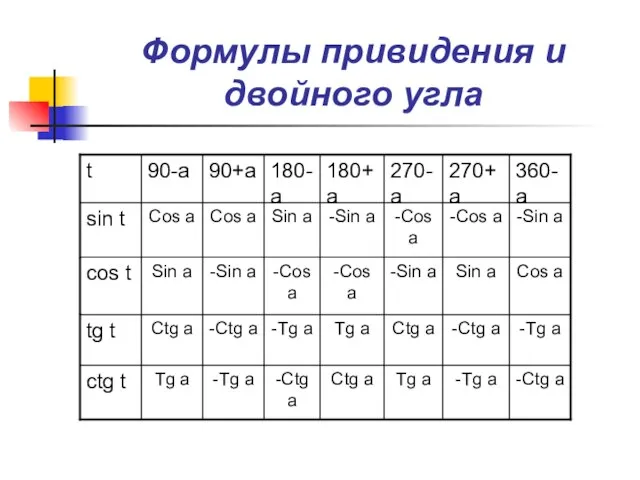
Формулы привидения и двойного угла