Анализ индексаДоу-Джонса

Анализ индекса Доу-Джонса
Задача 1.
Предпосылки регрессионного анализа: RS – критерий, равенство математического ожидания нулю, тест Гольдфельда-Куандта, тест Дарбина-Уотсона.
Запрограммировать предпосылки регрессионного анализа для упрощения вычисления.
Задача 2.
Написание статьи на тему «Анализ индекса Доу-Джонса»

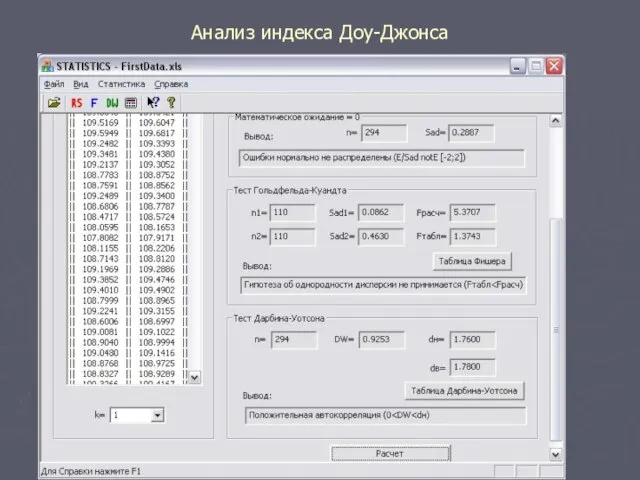
Анализ индекса Доу-Джонса
Программа «Предпосылки регрессионного анализа»
RS –Критерий.
Этот критерий численно равен отношению размаха вариации случайной величины к стандартному отклонению
Где ei - остатки, Sad - среднее квадратическое отклонение.
значение RS -критерия сравнивается с табличными верхними и нижними границами данного отношения, и если это значение не попадает в интервал между критическими границами, то с заданным уровнем значимости гипотеза о нормальности распределения отвергается, в противном случае принимается

Анализ индекса Доу-Джонса
Программа «Предпосылки регрессионного анализа»
Равенство математического ожидания нулю.
Случайная величина
Представляет собой единичные нормальные отклонения.
Если эти отклонения будут находиться в интервале [-2; 2], то можно говорить о том, что остатки нормально распределены. Т.е. , где математическое ожидание равно нулю. Это означает, что ошибки распределены по нормальному закону.

Анализ индекса Доу-Джонса
Программа «Предпосылки регрессионного анализа»
Тест Гольдфельда-Куандта.
Делим всю последовательность значений на 4:
где n - число наблюдений.
Обозначим полученные значения через L. Из середины исходной последовательности остатков выбрасываем L значений и оставшуюся последовательность значений делим на две подпоследовательности. Обозначим полученные подпоследовательности через: n1 и n2.
Для каждой подпоследовательности вычисляются остаточные суммы квадратов Qe1 и Qe2, и строится соотношение:
Далее ищется табличное значение распределения по Фишеру со степенями свободы f1=n1-k-1, f2=n2-k-1, где порядок рассматриваемой регрессионной модели. Если , то гипотеза об однородности дисперсии отклоняется (т.е. дисперсия гетероскедастична). В противном случае дисперсия является гомоскедастичной.

Анализ индекса Доу-Джонса
Программа «Предпосылки регрессионного анализа»
Тест Дарбина-Уотсона.
Данный тест выявляет наличие автокорреляции в ряде остатков.
Критерий Дарбина-Уотсона изменяется в диапазоне . При отсутствии автокорреляции DW=2. Если:
, есть положительная автокорреляция
, есть отрицательная автокорреляция,
, автокорреляция отсутствует,
или , нужны дополнительные исследования.
.

Анализ индекса Доу-Джонса

Анализ индекса Доу-Джонса
Статья.
В статье анализируется динамика первого в истории фондового индекса - индекса Доу-Джонса. Индекс Доу-Джонса - усредненный показатель динамики рыночной цены обращающихся на Нью-Йоркской фондовой бирже ценных бумаг. Являясь индексом биржевой конъюнктуры, индекс Доу-Джонса по существу отражает более точно, чем индексы, рассчитываемые на других мировых фондовых биржах , динамику предпринимательской активности и в этом качестве является ориентиром для бирж и в целом бизнеса всего мира.
Постановка задачи.
В данной статье рассматривается временной ряд, составленный из верхних значений индекса Доу-Джонса, взятый за год на период с 14 ноября 2005 по 13 ноября 2006 (показания являются ежедневными, в неделе 6 дней торгов).

Анализ индекса Доу-Джонса
Статья.
Выявляя структуру ряда, с помощью автокорреляции получили, что в ряде присутствует только линейная тенденция, так первый коэффициент корреляции значимый.
Линейные и нелинейные модели регрессии неадекватны, так как работают не более чем на 80%.
Авторегрессия первого порядка имеет следующий вид:
Авторегрессия работает на 96,3 %.
По RS-критерий получаем, что случайные компоненты распределены по нормальному закону.
Тест Гольфельда-Куандта показал, что дисперсия остатков гомоскедастична
Тест Дарбина-Уотсона выявил, что автокорреляция, т.е. зависимость, в остатках отсутствует.
Построили АРПСС(1,1,0) , она имеет следующий вид:
У построенной модели среднеквадратическая ошибка мала, она рана 0,49. Следовательно, можно сделать вывод о том, что АРПСС адекватна.

Анализ индекса Доу-Джонса
Статья.
Авторегрессия работает на 96,3 %.
По RS-критерий получаем, что случайные компоненты распределены по нормальному закону.
Тест Гольфельда-Куандта показал, что дисперсия остатков гомоскедастична
Тест Дарбина-Уотсона выявил, что автокорреляция, т.е. зависимость, в остатках отсутствует.
Построили АРПСС(1,1,0) , она имеет следующий вид:
У построенной модели среднеквадратическая ошибка мала, она рана 0,49. Следовательно, можно сделать вывод о том, что АРПСС адекватна.

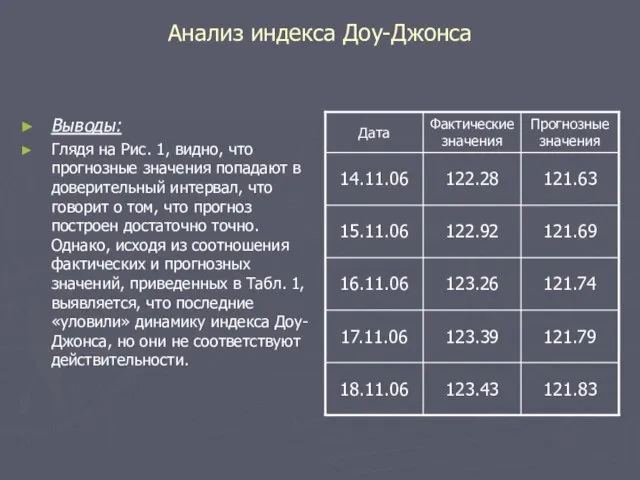
Анализ индекса Доу-Джонса
Выводы:
Глядя на Рис. 1, видно, что прогнозные значения попадают в доверительный интервал, что говорит о том, что прогноз построен достаточно точно. Однако, исходя из соотношения фактических и прогнозных значений, приведенных в Табл. 1, выявляется, что последние «уловили» динамику индекса Доу-Джонса, но они не соответствуют действительности.