Изображение пространственных фигур

Для изображения пространственных фигур используют параллельную проекцию. Плоскость, на которую проектируется фигура, называется плоскостью изображений, а сама проекция фигуры – изображением.

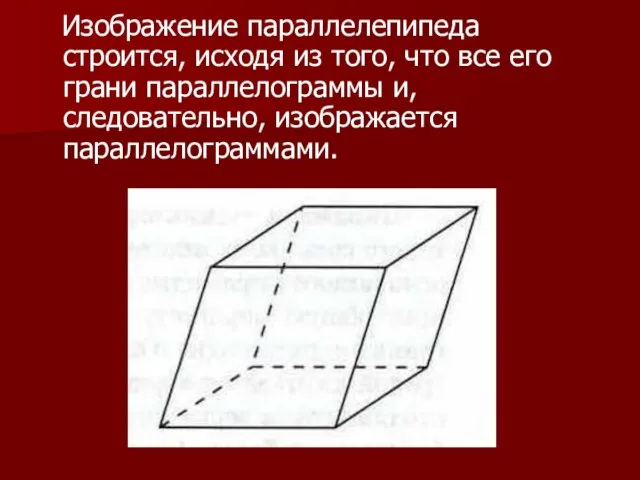
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображается параллелограммами.

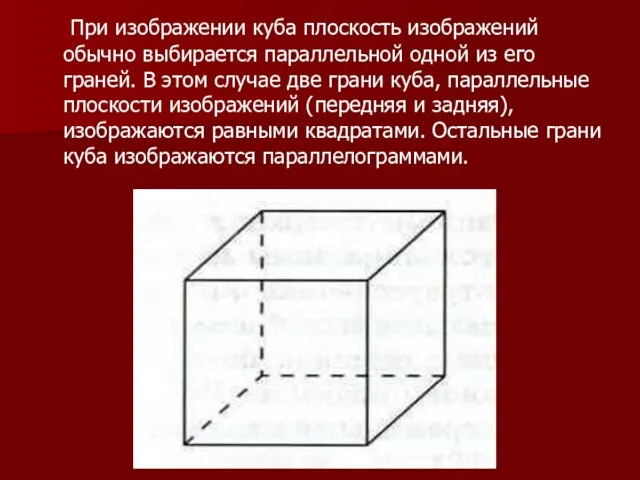
При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.

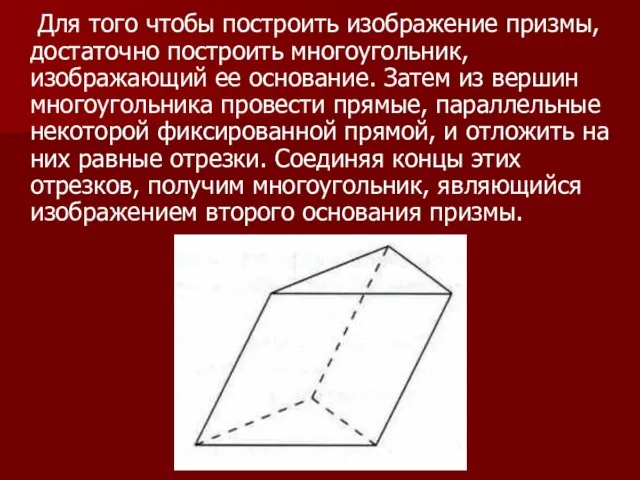
Для того чтобы построить изображение призмы, достаточно построить многоугольник, изображающий ее основание. Затем из вершин многоугольника провести прямые, параллельные некоторой фиксированной прямой, и отложить на них равные отрезки. Соединяя концы этих отрезков, получим многоугольник, являющийся изображением второго основания призмы.

Для того чтобы построить изображение пирамиды, достаточно построить многоугольник, изображающий ее основание. Затем выбрать какую-нибудь точку, которая будет изображать вершину пирамиды, и соединять ее с вершинами многоугольника. Полученные отрезки будут изображать боковые ребра пирамиды.

Плоское изображение, подчиняясь определенным законам, способно передать впечатление о трехмерном предмете. Однако при этом могут возникать иллюзии.
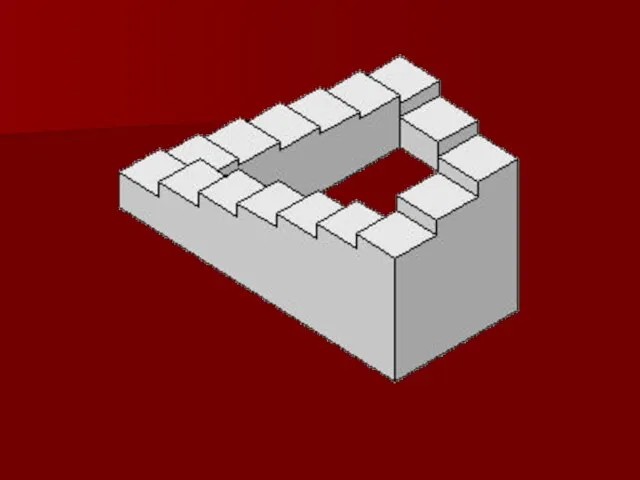
В живописи существует целое направление, которое называется импосибилизм (impossibility – невозможность) – изображение невозможных фигур, парадоксов.
Известный голландский художник М. Эшер (1898-1972) в гравюрах «Бельведер», «Водопад», «Поднимаясь и опускаясь» изобразил невозможные объекты.

Гравюра «Бельведер»

Гравюра «Водопад»

Гравюра «Поднимаясь и опускаясь»

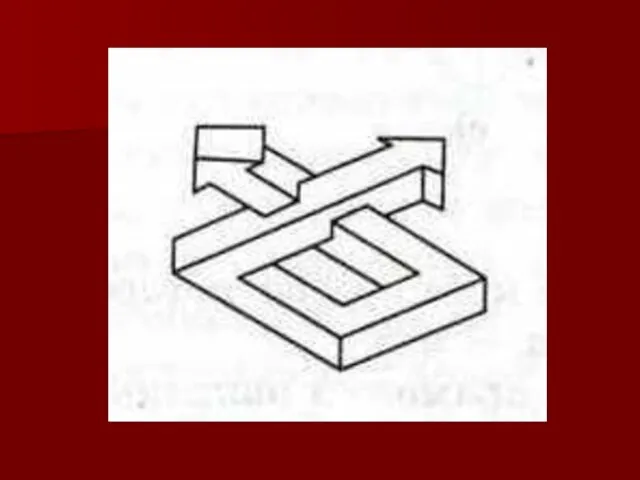
Современный шведский архитектор О. Рутерсвард посвятил невозможным объектам серию своих художественных работ.