Содержание
- 2. Арифметическая прогрессия – числовая последовательность, где каждый последующий член равен предыдущему, сложенным с одним и тем
- 3. 130; 118; 106; 94; 82;… an= an-1 + (-12) Формула, которая позволяет вычислить члены последовательности через
- 4. Разность арифметической прогрессии d > 0 прогрессия возрастающая, d
- 5. Доказать, что последовательность заданная формулой – арифметическая прогрессия. an =1,5 + 3n a n +1 =1,5+3(n+1)
- 6. Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Пример:
- 8. Скачать презентацию





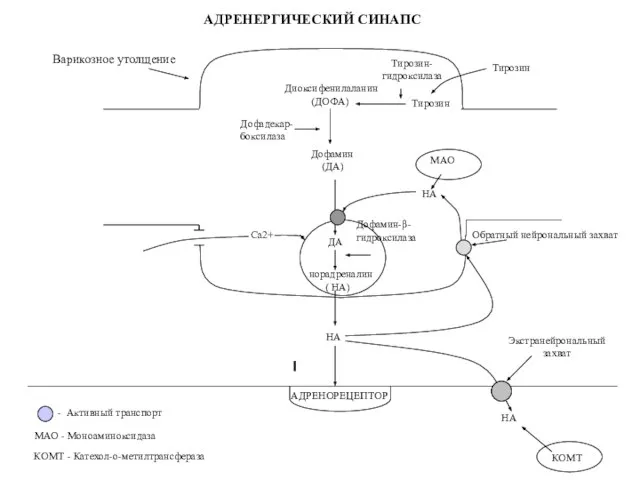 Адреномиметики
Адреномиметики Sport in Canada
Sport in Canada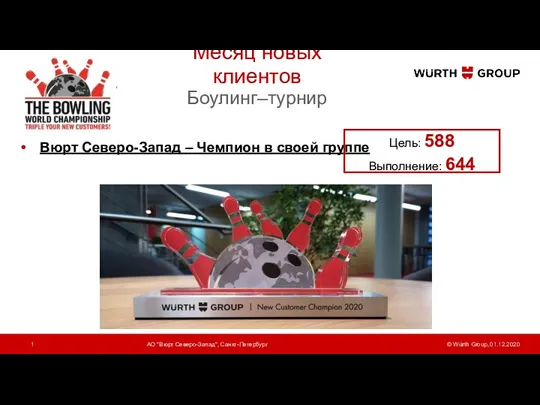 АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов
АО Вюрт Северо-Запад, Санкт-Петербург. Боулинг–турнир. Месяц новых клиентов Презентация на тему Русский герой сказок: Иван-дурак
Презентация на тему Русский герой сказок: Иван-дурак  Путешествие на водопад Атыш
Путешествие на водопад Атыш Помада Creamy Glam
Помада Creamy Glam Презентация по английскому Королевская семья Великобритании
Презентация по английскому Королевская семья Великобритании tema-gribi-rodnaya-tropinka_ru
tema-gribi-rodnaya-tropinka_ru Работа социального педагога с детьми имеющих отклоняющее поведение.
Работа социального педагога с детьми имеющих отклоняющее поведение. Комплекс упражнений утренней гимнастики
Комплекс упражнений утренней гимнастики Службы для электронного общения
Службы для электронного общения Характер и темперамент
Характер и темперамент Обществознание
Обществознание Материально-техническая база одно из условий эффективной реализации профильного обучения.
Материально-техническая база одно из условий эффективной реализации профильного обучения. Способ тепловой обработки сыпучих материалов и устройства для его осуществления
Способ тепловой обработки сыпучих материалов и устройства для его осуществления Архитектура Санкт-Петербурга
Архитектура Санкт-Петербурга project
project Greenway. Жизнь без химии с заботой о семье и природе
Greenway. Жизнь без химии с заботой о семье и природе Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16
Адрес: Тверская область, г. Нелидово Ул. Шахтерская 16 Сказочные птицы
Сказочные птицы Леонардо Да Винчи
Леонардо Да Винчи Как преодолеть стресс перед экзаменом
Как преодолеть стресс перед экзаменом Признаки нарушения адаптации в почерке
Признаки нарушения адаптации в почерке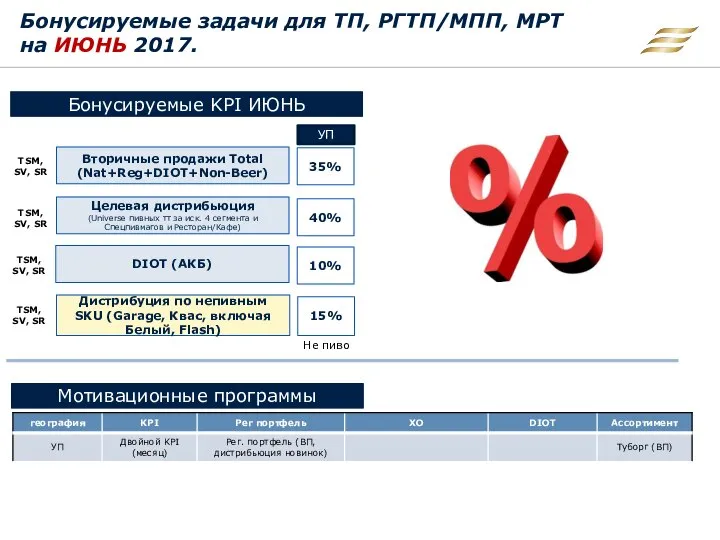 Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017
Бонусируемые задачи для ТП, РГТП/МПП, МРТ на июнь 2017 Доходы предприятия и финансовые результаты его деятельности
Доходы предприятия и финансовые результаты его деятельности Алтайский государственный университет
Алтайский государственный университет Методика оформление. Пушкинская карта
Методика оформление. Пушкинская карта Презентация на тему Социальная информатика
Презентация на тему Социальная информатика