Содержание
- 2. Углы, вписанные в окружность Презентацию подготовила учитель математики МОУ Поназыревская СОШ Орлова Н.В.
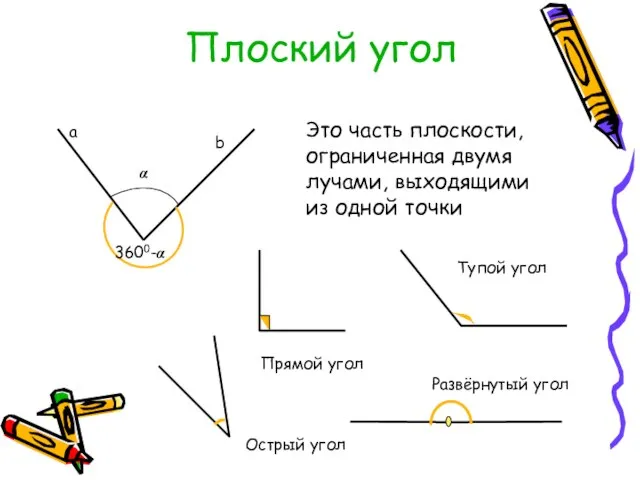
- 3. Плоский угол Это часть плоскости, ограниченная двумя лучами, выходящими из одной точки
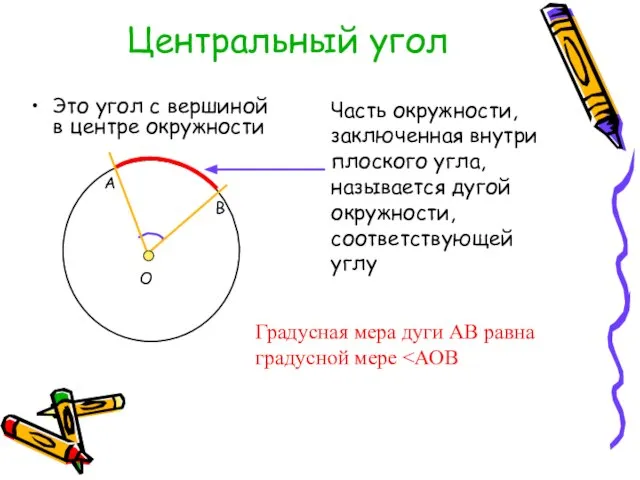
- 4. Центральный угол Это угол с вершиной в центре окружности Градусная мера дуги АВ равна градусной мере
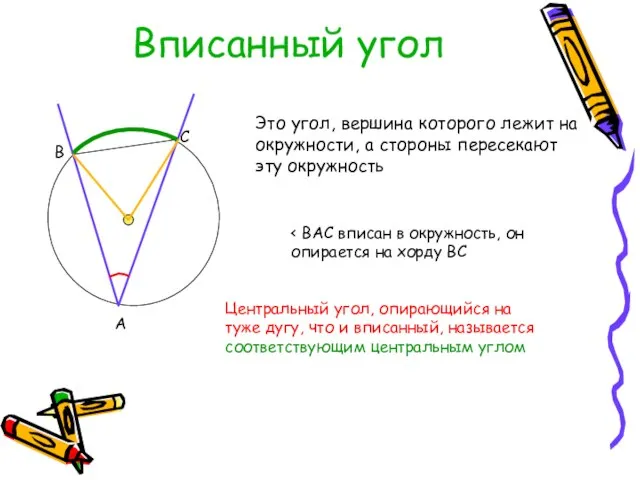
- 5. Вписанный угол Это угол, вершина которого лежит на окружности, а стороны пересекают эту окружность
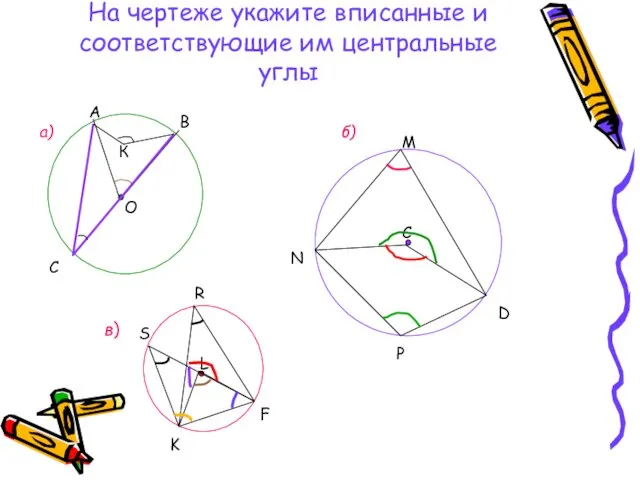
- 6. На чертеже укажите вписанные и соответствующие им центральные углы А В О К С а) б)
- 7. Свойство вписанного угла (теорема 11.5) Угол, вписанный в окружность , равен половине соответствующего центрального угла Дано:
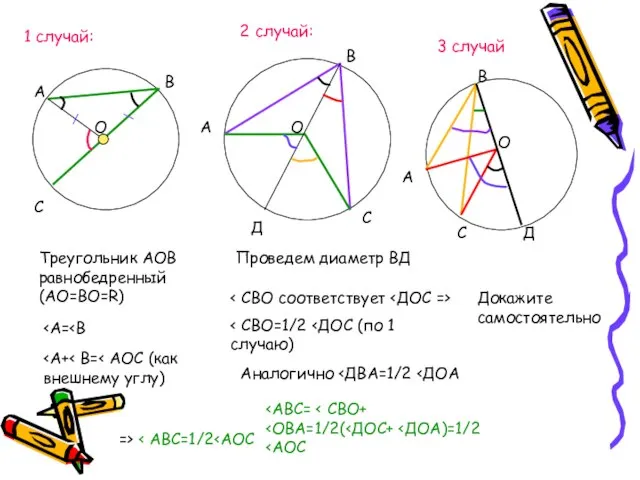
- 8. 1 случай: А В С О Треугольник АОВ равнобедренный (АО=ВО=R) => 2 случай: Проведем диаметр ВД
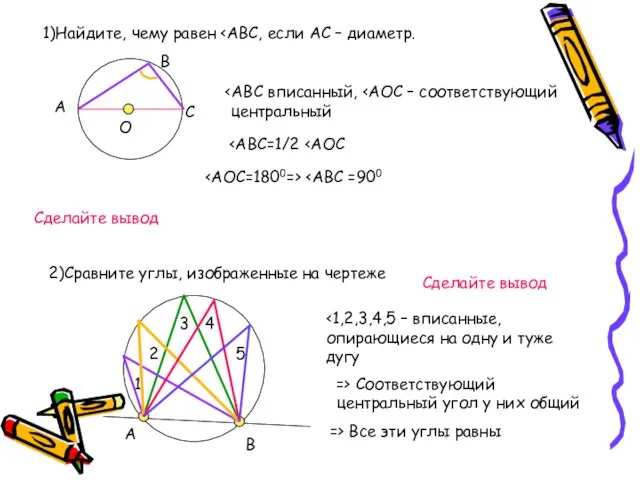
- 9. 1)Найдите, чему равен А В С О центральный Сделайте вывод 2)Сравните углы, изображенные на чертеже А
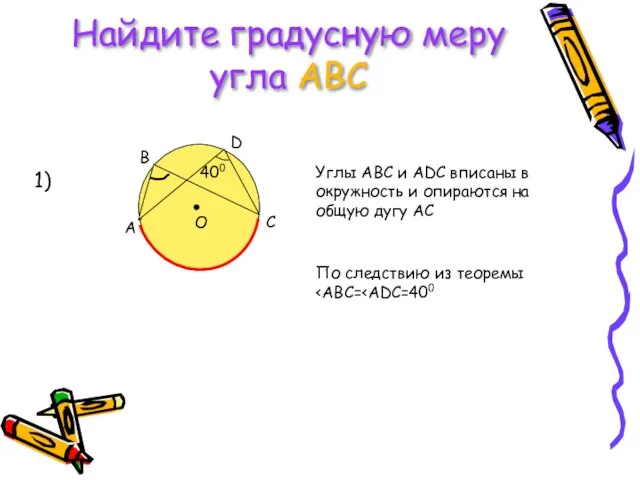
- 10. Найдите градусную меру угла АВС 1) Углы АВС и ADC вписаны в окружность и опираются на
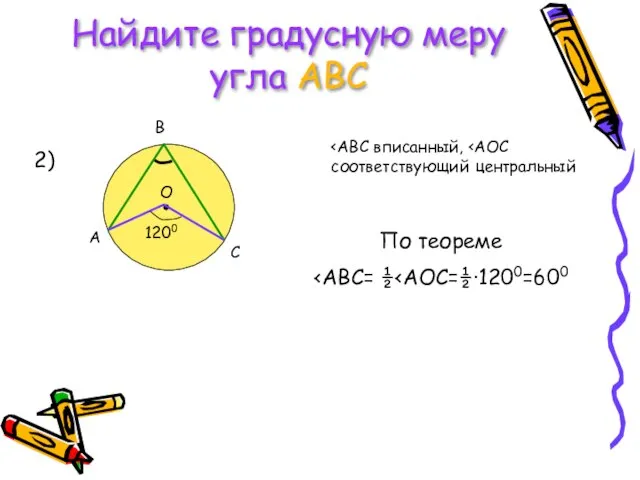
- 11. Найдите градусную меру угла АВС 2) По теореме
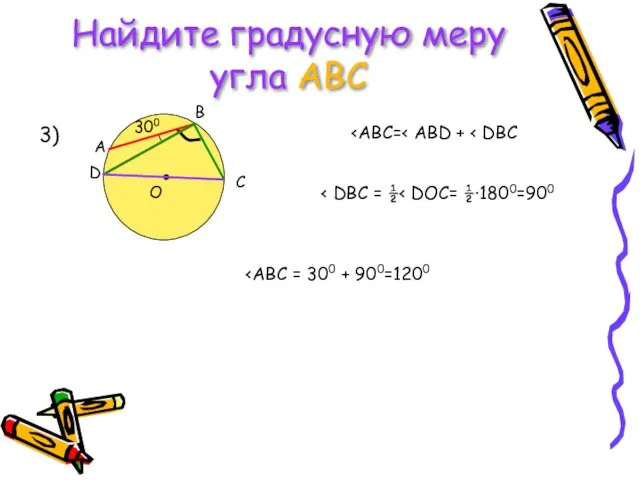
- 12. Найдите градусную меру угла АВС 3)
- 14. Скачать презентацию


 Курсовая работа. Создание декоративного натюрморта с передачей фактур в графике
Курсовая работа. Создание декоративного натюрморта с передачей фактур в графике England
England Формы работы, помогающие понять текст по стихотворению А.Блока «Летний вечер»
Формы работы, помогающие понять текст по стихотворению А.Блока «Летний вечер» Культура и традиции мордовского народа
Культура и традиции мордовского народа Почему нельзя не проветривать кабинет?
Почему нельзя не проветривать кабинет? Новый взгляд на экономическую географию
Новый взгляд на экономическую географию Презентация на тему Внутреннее строение млекопитающих
Презентация на тему Внутреннее строение млекопитающих Оживший Бог войны Арес - неукротимый бог войны
Оживший Бог войны Арес - неукротимый бог войны Гендерная статистика ЕГЭ по техническим предметам
Гендерная статистика ЕГЭ по техническим предметам Законы сохранения в механике
Законы сохранения в механике РДУ-99. Его значение и применение
РДУ-99. Его значение и применение India - English Transit
India - English Transit Презентация на тему Драгоценные камни
Презентация на тему Драгоценные камни 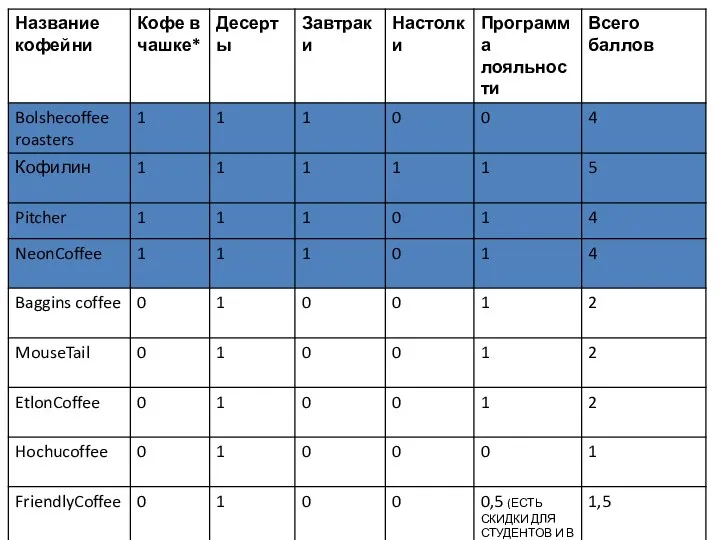 4. карта позиционирования, конкуренты_Шашина_3ГИВ13
4. карта позиционирования, конкуренты_Шашина_3ГИВ13 Cтратегия пенсионного обеспечения граждан в условиях ухудшающейся демографии: неизбежность или вызов
Cтратегия пенсионного обеспечения граждан в условиях ухудшающейся демографии: неизбежность или вызов Профессиональная ориентация в контексте постсовременности Опыт реализации компьютерно-опосредованных средств профессиональн
Профессиональная ориентация в контексте постсовременности Опыт реализации компьютерно-опосредованных средств профессиональн Конкурс среди молодых семей «Семь Я»
Конкурс среди молодых семей «Семь Я» Ваше название
Ваше название Изготовление аксессуара Цветок
Изготовление аксессуара Цветок Intelligent efficiency. Готовый набор инструментов для анализа и принятия решений
Intelligent efficiency. Готовый набор инструментов для анализа и принятия решений Президентские состязания 2011-2012 учебный год МБОУ «Кваркенская СОШ»
Президентские состязания 2011-2012 учебный год МБОУ «Кваркенская СОШ» Информация о регулируемой деятельности ООО Томскводоканал в сфере водоснабжения и водоотведения
Информация о регулируемой деятельности ООО Томскводоканал в сфере водоснабжения и водоотведения Специальность «Режиссер шоу-программ и театрализованных представлений»
Специальность «Режиссер шоу-программ и театрализованных представлений» Врачебный диагноз
Врачебный диагноз Привлечение средств от приносящей доход деятельности
Привлечение средств от приносящей доход деятельности Кукольный театр
Кукольный театр Большой, красивый, уютный.
Большой, красивый, уютный. Париж
Париж