Классификация мер информации

Классификация мер информации
Синтаксическая мера информации
Семантическая мера информации
Прагматическая мера информации

Единицы измерения информации
1 бит = кол-во двоичных цифр (0 и 1)
Пример: код 11001011 имеет объем данных V= 8 бит
1 байт = 8 бит
1 Кбайт = 1024 байт = 210 байт
1 Мбайт = 1024 Кбайт = 220 байт =1 048 576 байт;
1 Гбайт = 1024 Мбайт = 230 байт = 1 073 741 824 байт;
1 Тбайт = 1024 Гбайт = 240 байт = 1 099 511 627 776 байт.

Вероятностный подход
События, о которых нельзя сказать произойдут они или нет, пока не будет осуществлен эксперимент, называются случайными.
Отдельный повтор случайного события называется опытом, а интересующий нас исход этого опыта – благоприятным.
Если N – общее число опытов, а NА - количество благоприятных исходов случайного события А, то отношение NA/ N, называется относительной частотой появления события А.
В разных сериях опытов частота может быть различна, но при увеличении количества опытов относительная частота все меньше отклоняется от некоторой константы, ее наличие называется статической устойчивостью частот.
Если все исходы опыта конечны и равновозможные, то их вероятность равна
где n - число исходов.

Энтропия (часть1)
Энтропия – численная мера измеряющая неопределенность.
Некоторые свойства функции:
f (1)=0, так как при n=1 исход не является случайным и неопределенность отсутствует.
f (n) возрастает с ростом n, чем больше возможных исходов, тем труднее предсказать результат.
Если a и b два независимых опыта с количеством равновероятных исходов na и nb , то мера их суммарной неопределенности равна сумме мер неопределенности каждого из опытов:
За количество информации - разность неопределенностей “ДО” и ”ПОСЛЕ” опыта:

общее число исходов
М – число попыток (пример: Х = 62 = 36)
Энтропия системы из М бросаний кости будет в M раз больше, чем энтропия системы однократного бросания кости - принцип аддитивности энтропии:
Энтропия (часть 2)

Обозначим через K
Получим f(X) = K ∙ lnX или H = K ∙ lnX, таким образом получим формулу Хартли для равновозможных исходов
Формула Шеннона для неравновозможных исходов
Формула Хартли и Шеннона

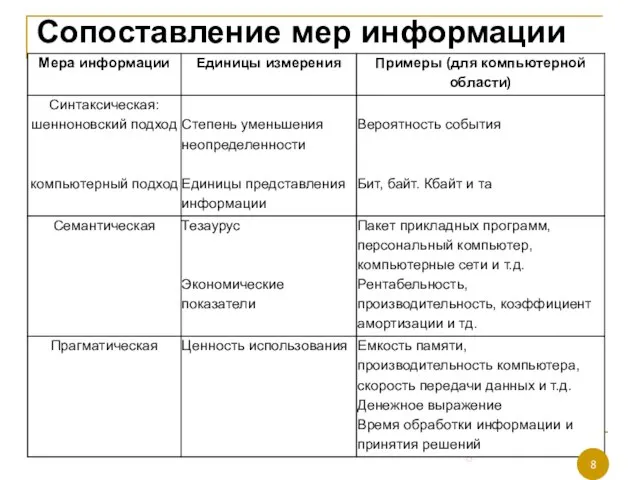
Сопоставление мер информации

Кодирование информации.
Информатика

Абстрактный алфавит
Алфавит - множество знаков, в котором определен их порядок (общеизвестен порядок знаков в русском алфавите: А, Б,..., Я)
Алфавит прописных русских букв
Алфавит Морзе
Алфавит клавиатурных символов ПЭВМ IBM (русифицированная клавиатура)
Алфавит знаков правильной шестигранной игральной кости
Алфавит арабских цифр
Алфавит шестнадцатиричных цифр
Алфавит двоичных цифр
Двоичный алфавит «точка, «тире»
Двоичный алфавит «плюс», «минус»
Алфавит прописных латинских букв
Алфавит римской системы счисления
Алфавит языка блок-схем изображения алгоритмов
Алфавит языка программирования

Математическая постановка задачи кодирования
А - первичный алфавит. Состоит из N
знаков со средней информацией на знак IА .
В - вторичный алфавит из М знаков со средней
информацией на знак IВ .
Сообщение в первичном алфавите
содержит n знаков, а закодированное – m
знаков.
Is (A)-информация в исходном сообщении,
If (B)-информация в закодированном сообщении.

IS (A) ≤ If (B) – условие обратимости кодирования, т.е не исчезновения информации.
n* IА ≤ m* IB (заменили произведением числа знаков на среднее информационное содержание знака).
m/n –характеризует среднее число знаков вторичного алфавита, который используется для кодирования одного знака первичного. Обозначим его К (А, В)
К (А, В)≥ I (A) / I (B) Обычно К (А, В) >1
Кmin (А, В)= I (A) / I (B) – минимальная длинна кода
Математическая постановка задачи кодирования

Первая теорема Шеннона
Примером избыточности может служить предложение
«в словох всо глосноо зомононо боквой о»
Существует возможность создания системы эффективного кодирования дискретных сообщений, у которой среднее число двоичных символов на один символ сообщения асимптотически стремится к энтропии источника сообщений .
Х = {xi } - кодирующее устройство – В
Требуется оценить минимальную среднюю длину кодовой комбинации.
Шенноном была рассмотрена ситуация, когда при кодировании сообщения в первичном алфавите учитывается различная вероятность появления знаков, а также равная вероятность появления знаков вторичного алфавита.
Тогда:
где I (A) - средняя информация на знак первичного алфавита.

Вторая теорема Шеннона
При наличии помех в канале всегда можно найти такую систему кодирования, при которой сообщения будут переданы с заданной достоверностью. При наличии ограничения пропускная способность канала должна превышать производительность источника сообщений.
Первоначально последовательность Х = {xi} кодируется символами из В так, что достигается максимальная пропускная способность (канал не имеет помех).
Затем в последовательность из В длины n вводится r символов и по каналу передается новая последовательность из n + r символов. Число возможных последовательностей длины n + r больше числа возможных последовательностей длины n. Множество всех последовательностей длины n + r может быть разбито на n подмножеств, каждому из которых сопоставлена одна из последовательностей длины n. При наличии помехи на последовательность из n + r символов выводит ее из соответствующего подмножества с вероятностью сколь угодно малой.
Это позволяет определять на приемной стороне канала, какому подмножеству принадлежит искаженная помехами принятая последовательность длины n + r, и тем самым восстановить исходную последовательность длины n.

Вторая теорема Шеннона
Это позволяет определять на приемной стороне канала, какому подмножеству принадлежит искаженная помехами принятая последовательность длины п + r, и тем самым восстановить исходную последовательность длины п.
Эта теорема не дает конкретного метода построения кода, но указывает на пределы достижимого в создании помехоустойчивых кодов, стимулирует поиск новых путей решения этой проблемы.
Способ кодирования только устанавливает факт искажения сообщения, что позволяет потребовать повторную передачу.
Используемый код находит и автоматически исправляет ошибку передачи.