Меры информации

Наука исследования свойств знаков и систем
Семиотика (греч. semeion – знак, признак) - наука, занимающаяся исследованием свойств знаков и знаковых систем.
Семиотика выделяет следующие уровни передачи информации:
Синтаксический, рассматриваются внутренние свойства сообщений.
Семантический, анализируется смысловое содержание сообщения, его отношение к источнику информации
Прагматический, рассматривается потребительское содержание сообщения, его отношение к получателю.

Синтаксический уровень
Идея: Это технические проблемы совершенствования методов передачи сообщений и их материальных носителей - сигналов. Проблемы доставки получателю сообщений. Полностью абстрагируются от смыслового содержания сообщений и их целевого предназначения
Информация - данные
Учитывают:
Тип носителя
Способ представления информации
Скорость передачи и обработки
Размеры кодов представления информации и т.д.

Семантический уровень
Идея: Проблемы связаны с формализацией и учетом смысла передаваемой информации. Проблемы этого уровня чрезвычайно сложны, так как смысловое содержание информации больше зависит от получателя, чем от семантики сообщения, представленного на каком-либо языке.
На данном уровне:
Анализируется сведенья, которые отражает информация
Выявляется смысл информации
Выявляется содержание информации
Осуществляется обобщение

Прагматический уровень
Идея: Проблемы этого уровня связаны с определением ценности и полезности информации для потребителя. Интересуют последствия от получения и использования данной информации потребителем.
На данном уровне:
Ценность информации может быть различной для разных потребителей.
Фактор доставки актуальности доставки и использования.

Классификация мер информации
Синтаксическая мера информации
Семантическая мера информации
Прагматическая мера информации

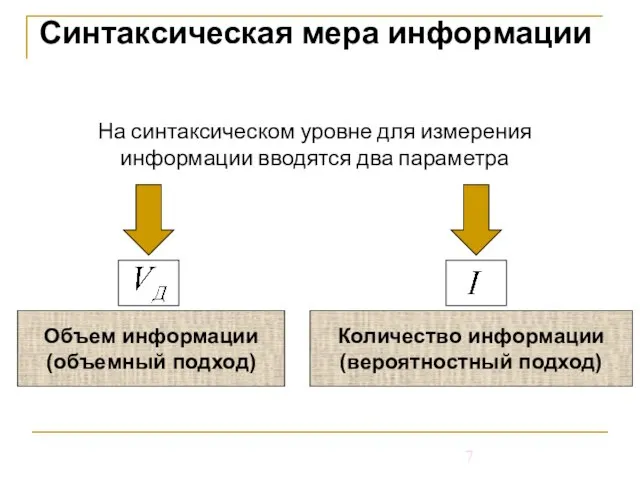
На синтаксическом уровне для измерения информации вводятся два параметра
Синтаксическая мера информации
Объем информации
(объемный подход)
Количество информации
(вероятностный подход)

Объемный подход ( VД )
Идея: Если количество информации, содержащейся в сообщении из одного символа, принять за единицу, то объем информации (данных) VД в любом другом сообщении будет равен количеству символов (разрядов) в этом сообщении. В памяти компьютера объем информации записывается двоичными знаками и равен количеству требуемых для этой записи двоичных кодов.
Объём данных ( VД ) в техническом смысле этого слова как информационный объём сообщения или как объём памяти, необходимый для хранения сообщения без каких-либо изменений.

Единицы измерения информации
1 бит = кол-во двоичных цифр (0 и 1)
Пример: код 11001011 имеет объем данных V= 8 бит
1 байт = 8 бит
1 Кбайт = 1024 байт = 210 байт*
1 Мбайт = 1024 Кбайт = 220 байт =1 048 576 байт;
1 Гбайт = 1024 Мбайт = 230 байт = 1 073 741 824 байт;
1 Тбайт = 1024 Гбайт = 240 байт = 1 099 511 627 776 байт.

Вероятностный подход
События, о которых нельзя сказать произойдут они или нет, пока не будет осуществлен эксперимент, называются случайными.
Отдельный повтор случайного события называется опытом, а интересующий нас исход этого опыта – благоприятным.
Если N – общее число опытов, а NА - количество благоприятных исходов случайного события А, то отношение NA/ N, называется относительной частотой появления события А.
В разных сериях опытов частота может быть различна, но при увеличении количества опытов относительная частота все меньше отклоняется от некоторой константы, ее наличие называется статической устойчивостью частот.
Если все исходы опыта конечны и равновозможные, то их вероятность равна
где n - число исходов.

Энтропия (часть1)
Энтропия – численная мера измеряющая неопределенность.
Некоторые свойства функции:
f (1)=0, так как при n=1 исход не является случайным и неопределенность отсутствует.
f (n) возрастает с ростом n, чем больше возможных исходов, тем труднее предсказать результат.
Если a и b два независимых опыта с количеством равновероятных исходов na и nb , то мера их суммарной неопределенности равна сумме мер неопределенности каждого из опытов:
За количество информации - разность неопределенностей “ДО” и ”ПОСЛЕ” опыта:

общее число исходов
М – число попыток (пример: Х = 62 = 36)
Энтропия системы из М бросаний кости будет в M раз больше, чем энтропия системы однократного бросания кости - принцип аддитивности энтропии:
Энтропия (часть 2)

Обозначим через K
Получим f(X) = K ∙ lnX или с учетом (1): H = K ∙ lnN, таким образом получим формулу Хартли для равновозможных исходов
Формула Шеннона для неравновозможных исходов
Формула Хартли и Шеннона

Количество информации (в битах), заключенное в двоичном слове, равно числу двоичных знаков в нем.
Энтропия (часть 3)
Информация – это содержание сообщения, понижающего
неопределенность некоторого опыта с неоднозначным исходом; убыль связанной с ним энтропии является количественной мерой информации.

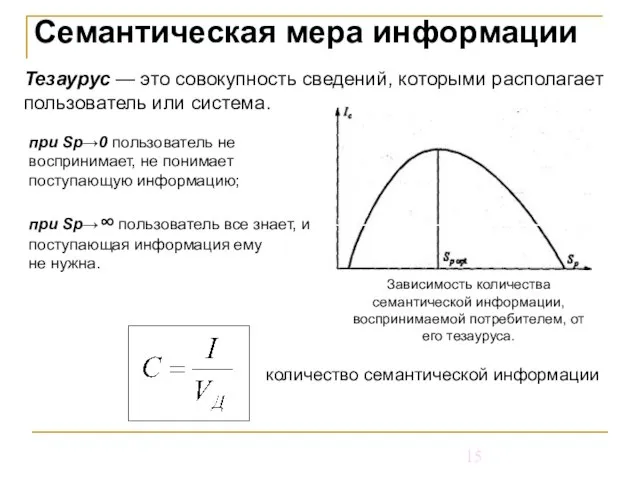
Семантическая мера информации
Тезаурус — это совокупность сведений, которыми располагает пользователь или система.
Зависимость количества семантической информации, воспринимаемой потребителем, от его тезауруса.
количество семантической информации
при Sp→0 пользователь не
воспринимает, не понимает
поступающую информацию;
при Sp→∞ пользователь все знает, и поступающая информация ему
не нужна.

Прагматическая мера информации
Эта мера определяет полезность информации (ценность) для достижения пользователем поставленной цели. Эта мера также величина относительная, обусловленная особенностями использования этой информации в той или иной системе.
Ценность информации целесообразно измерять в тех же самых единицах (или близких к ним), в которых измеряется целевая функция.
Целевая функция - есть математическое выражение некоторого критерия качества одного объекта (решения, процесса и т.д.) в сравнении с другим.

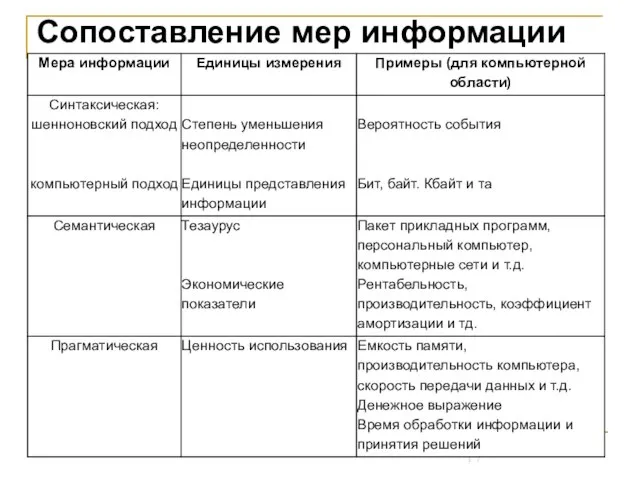
Сопоставление мер информации

Кодирование информации.
Информатика

Абстрактный алфавит
Алфавит - множество знаков, в котором определен их порядок (общеизвестен порядок знаков в русском алфавите: А, Б,..., Я)
Алфавит прописных русских букв
Алфавит Морзе
Алфавит клавиатурных символов ПЭВМ IBM (русифицированная клавиатура)
Алфавит знаков правильной шестигранной игральной кости
Алфавит арабских цифр
Алфавит шестнадцатиричных цифр
Алфавит двоичных цифр
Двоичный алфавит «точка, «тире»
Двоичный алфавит «плюс», «минус»
Алфавит прописных латинских букв
Алфавит римской системы счисления
Алфавит языка блок-схем изображения алгоритмов
Алфавит языка программирования

Кодирование информации.
Источник представляет сообщение в алфавите, который называется
первичным, далее это сообщение попадает в устройство,
преобразующее и представляющее его во вторичном алфавите.
Код – правило, описывающее соответствие знаков (или их сочетаний) первичного алфавита знаком (их сочетаниями) вторичного алфавита.
Кодирование – перевод информации, представленной сообщением в первичном алфавите, в последовательность кодов.
Декодирование – операция обратная кодированию.
Кодер – устройство, обеспечивающее выполнение операции кодирования.
Декодер – устройство, производящее декодирование.
Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечит возврат к исходной информации без каких-либо ее потерь.

Математическая постановка задачи кодирования
А - первичный алфавит. Состоит из N
знаков со средней информацией на знак IА .
В- вторичный алфавит из М знаков со средней
информацией на знак IВ .
Сообщение в первичном алфавите
содержит n знаков, а закодированное – m
знаков.
Is (A)-информация в исходном сообщении,
If (B)-информация в закодированном сообщении.

IS (A) ≤ If (B) – условие обратимости кодирования, т.е не исчезновения информации.
n* IА ≤ m* IB (заменили произведением числа знаков на среднее информационное содержание знака).
m/n –характеризует среднее число знаков вторичного алфавита, который используется для кодирования одного знака первичного. Обозначим его К (А, В)
К (А, В)≥ I (A) / I (B) Обычно К (А, В) >1
Кmin (А, В)= I (A) / I (B) – минимальная длинна кода
Математическая постановка задачи кодирования

Первая теорема Шеннона
Примером избыточности может служить предложение
«в словох всо глосноо зомононо боквой о»
Существует возможность создания системы эффективного кодирования дискретных сообщений, у которой среднее число двоичных символов на один символ сообщения асимптотически стремится к энтропии источника сообщений .
Х = {xi } - кодирующее устройство – В
Требуется оценить минимальную среднюю длину кодовой комбинации.
Шенноном была рассмотрена ситуация, когда при кодировании сообщения в первичном алфавите учитывается различная вероятность появления знаков, а также равная вероятность появления знаков вторичного алфавита.
Тогда:
где I (A) - средняя информация на знак первичного алфавита.

Вторая теорема Шеннона
При наличии помех в канале всегда можно найти такую систему кодирования, при которой сообщения будут переданы с заданной достоверностью. При наличии ограничения пропускная способность канала должна превышать производительность источника сообщений.
Первоначально последовательность Х = {xi} кодируется символами из В так, что достигается максимальная пропускная способность (канал не имеет помех).
Затем в последовательность из В длины n вводится r символов и по каналу передается новая последовательность из n + r символов. Число возможных последовательностей длины n + т больше числа возможных последовательностей длины n. Множество всех последовательностей длины n + r может быть разбито на n подмножеств, каждому из которых сопоставлена одна из последовательностей длины n. При наличии помехи на последовательность из n + r символов выводит ее из соответствующего подмножества с вероятностью сколь угодно малой.
Это позволяет определять на приемной стороне канала, какому подмножеству принадлежит искаженная помехами принятая последовательность длины n + r, и тем самым восстановить исходную последовательность длины n.

Вторая теорема Шеннона
Это позволяет определять на приемной стороне канала, какому подмножеству принадлежит искаженная помехами принятая последовательность длины п + r, и тем самым восстановить исходную последовательность длины п.
Эта теорема не дает конкретного метода построения кода, но указывает на пределы достижимого в создании помехоустойчивых кодов, стимулирует поиск новых путей решения этой проблемы.

Вторая теорема Шеннона
способ кодирования только устанавливает факт искажения сообщения, что позволяет потребовать повторную передачу;
используемый код находит и автоматически исправляет ошибку передачи.

Особенности вторичного алфавита при кодировании
Элементарные коды 0 и 1 могут иметь одинаковые длительности (t0 = t1) или разные (≠).
Длина кода может быть одинаковой для всех знаков первичного алфавита (код равномерный) или различной (неравномерный код)
Коды могут строиться для отдельного знака первичного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов).

Равномерное алфавитное кодирование.
Представление чисел в компьютере
Компьютерный алфавит С включает буквы латинского алфавита – 52 шт.
Букв русского (прописные и строчные) – 66 шт.
Цифры 0…9 – 10 шт.
Знаки математических операций, препинания, спецсимволы – 20 штук
Итого: 148

К (С, 2) ≥ log2 148 ≥ 7,21,
так как длина кода – целое число, следовательно,
К (С,2) = 8бит = 1байт.
Именно такой способ кодирования принят в компьютерных системах. Один байт соответствует количеству информации в одном знаке алфавита при их равновероятном распределении.
Это объемный способ измерения информации.
Присвоение символу конкретного двоичного кода
фиксируется в кодовой таблице, где устанавливается
соответствие между символами и их порядковыми номерами.

Таблицы кодировки
Таблица, в которой устанавливается однозначное соответствие между символами и их порядковыми номерами, называется таблицей кодировки.
Для разных типов ЭВМ используют различные таблицы кодировки:
ANSI - (American National Standards Institute)
ASCII - (American Standard Cod for Information Interchange)

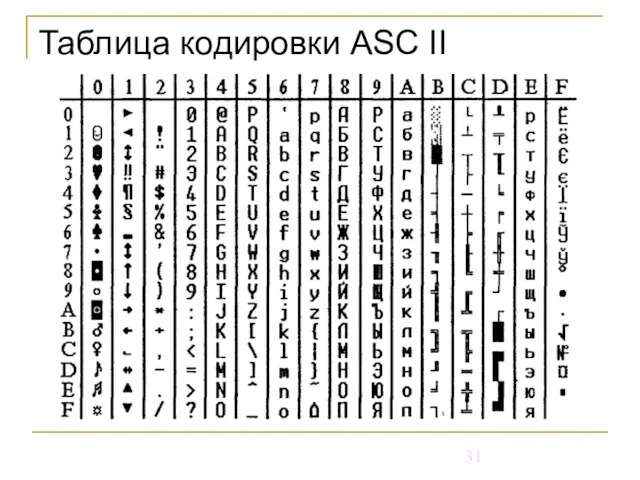
Таблица кодировки ASC ІІ

Код обмена информации ASC ІІ
Первоначально – 7 бит
N=27=128 символов
0…31- всевозможные управляющие символы
32…127 – видимые на экране символы.
Сейчас – 8 бит
N=28 =256 символов
128…255- национальные алфавиты,псевдографика
01000001 = буква А = 65

Системы кодирования
КОИ-7
Windows-1251
КОИ-8
ISO
Unicode

Кодирование текстовой информации

Кодирование графической информации*
Растровое изображение представляет собой однослойную сетку точек, называемых пикселами (pixel, от англ. picture element). Код пиксела содержит информации о его цвете.
Векторное изображение многослойно. Каждый элемент векторного изображения - линия, прямоугольник, окружность или фрагмент текста - располагается в своем собственном слое, пикселы которого устанавливаются независимо от других слоев.
Объем графического файла в битах определяется как произведение количества пикселей на разрядность цвета (битовую глубину)

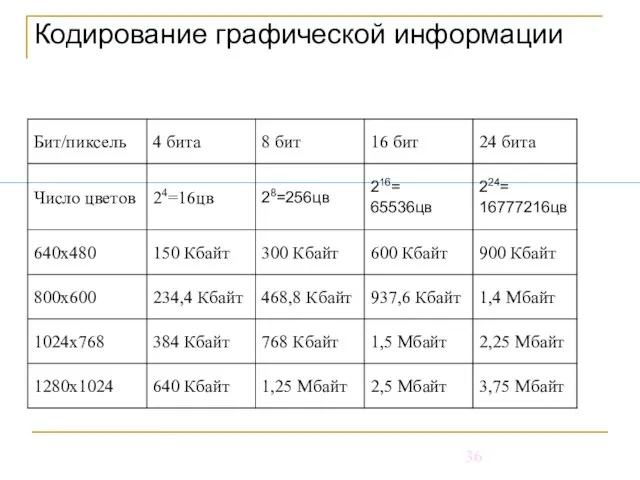
Кодирование графической информации

Кодирование звука*
Звук - это колебания воздуха
Процесс преобразования аналогового сигнала в последовательность двоичных чисел называется дискретизацией (или оцифровкой), а устройство, выполняющее его - аналого-цифровым преобразователем (АЦП).
Для того чтобы воспроизвести закодированный таким образом звук, нужно выполнить обратное преобразование (для него служит цифро-аналоговый преобразователь -- ЦАП), а затем сгладить получившийся ступенчатый сигнал.

Кодирование видеоинформации*
Число кадров вычисляется как произведение длительности видеоклипа на скорость кадров , то есть их количество в 1 с
При разрешении 800*600 точек, разрядности цвета C=16, скорости кадров v=25 кадров/c, видеоклип длительностью 30 с будет иметь объем:
V=800*600*16*25*30=576*107(бит)=72*107(байт)=687(Мбайт)