Слайд 2Кластеризация – это разбиение элементов некоторого множества
на группы на основе их

схожести. Задача кластеризации состоит в
разбиении объектов из X на несколько подмножеств (кластеров),
в которых объекты более схожи между собой, чем с объектами
из других кластеров. В метрическом пространстве «схожесть» обычно определяют через расстояние.
Алгоритмы кластеризации оперируют с объектами. Каждому объекту Х отождествляется вектор характеристик . Компоненты , являются отдельными характеристиками объекта. Количество характеристик d определяет размерность пространства характеристик.
Множество, состоящее из всех векторов характеристик, обозначается , где .
Слайд 3Кластер представляет собой подмножество «близких друг к другу» объектов из М. Расстояние

между объектами и определяется на основе выбранной метрики в пространстве характеристик.
Существует множество методов кластеризации, которые можно классифицировать на четкие и нечеткие.
Четкие методы кластеризации разбивают исходное множество объектов X на несколько непересекающихся подмножеств. При этом любой объект из X принадлежит только одному кластеру.
Нечеткие методы кластеризации позволяют одному и тому же объекту принадлежать одновременно нескольким (или даже всем) кластерам, но с различной степенью принадлежности. Нечеткая кластеризация во многих ситуациях более "естественна", чем четкая, например, для объектов, расположенных на границе кластеров.
Слайд 4Четкая (непересекающаяся) кластеризация – кластеризация, в которой каждый объект из М относится

только к одному кластеру.
Нечеткая кластеризация – кластеризация, при которой для каждого из М определяется - вещественное значение, показывающее степень принадлежности к кластеру .
Развитие и широкое применение нечёткая кластеризация получила благодаря Бездеку и его методу нечетких k-средних (Fuzzy c-means - FCM).
Слайд 5Базовый алгоритм нечетких k-средних
Самый простой алгоритм нечеткой кластеризации – это нечеткий алгоритм

k-средних. Этот алгоритм находит компактные кластеры, например, сферической формы.
Нечеткие кластеры опишем матрицей нечеткого разбиения , , , где -я строчка содержит степени принадлежности объекта кластерам . Единственным отличием матрицы степеней принадлежности четкого разбиения от нечеткого является то, что элементы матрицы принимают значения из двухэлементного множества {0,1}, а не из интервала [0,1].
Слайд 6В базовом алгоритме нечетких k-средних расстояние между объектом и центром кластера рассчитывается

через стандартную Евклидову норму: .
В результате алгоритмов кластеризации с фиксированной нормой форма всех кластеров получается одинаковой. Алгоритмы кластеризации как бы навязывают данным неприсущую им структуру, что приводит не только к неоптимальным, но иногда и к принципиально неправильным результатам. Для устранения этого недостатка предложено несколько методов, среди которых выделим алгоритм Густафсона-Кесселя (Gustafson-Kessel algorithm).
Слайд 7Алгоритм Густафсона-Кесселя(Gustafson – Kessel, GK)
По отношению к обычному алгоритму k-средних главное изменение

состоит во введении в формулу расчета расстояния между векторами масштабирующей матрицы A. В качестве масштабирующей обычно применяется симметричная положительно определенная матрица, т.е. матрица, у которой все собственные значения являются действительными и положительными.
Алгоритм Густафсона-Кесселя использует адаптивную норму для каждого кластера, т.е. для каждого j-го кластера существует своя норм-порождающая матрица . В этом алгоритме при кластеризации оптимизируются не только координаты центров кластеров и матрица нечеткого разбиения, но также и норм-порождающие матрицы для всех кластеров. Это позволяет выделять кластера различной геометрической формы.
GK – простой нечеткий алгоритм кластеризации, позволяющий обнаружить кластеры эллипсоидальной формы. В комбинации с алгоритмом нечетких k – средних он часто используется, чтобы инициализировать другие нечеткие алгоритмы кластеризации.
Слайд 12Алгоритм нечетких с-эллипсоидов
Шаг 1. Установить параметры алгоритма:
c - количество кластеров; m - экспоненциальный вес;
-

параметр остановки алгоритма.
Шаг 2. Случайным образом сгенерировать матрицу нечеткого разбиения .
Шаг 3. Рассчитать центры кластеров:
Шаг 4. Рассчитать расстояния между объектами из X и центрами кластеров:
где евклидово расстояние s=1,..,r, r-количество собственных векторов, - s-ый собственный вектор ковариационной матрицы кластера j.
Параметр , где max и min собственное значение матрицы .
Слайд 13Алгоритм нечетких с-эллипсоидов
Шаг 5. Пересчитать элементы матрицы нечеткого разбиения:
если
если :
Шаг 6. Проверить условие ,

где - матрица нечеткого разбиения на предыдущей итерации алгоритма. Если "да", то перейти к шагу 7, иначе - к шагу 3.
Шаг 7. Конец.
Слайд 14Shell-clustering algorithm
Основное новшество алгоритма состоит в том, что в данном алгоритме прототип

кластера описывается помимо центра ещё и радиусом .
Формула для вычисления расстояния имеет следующий вид:
Слайд 16FCM algorithm
GK-algorithm
Результаты для окружностей
С-elliptotypes
Shell-clustering
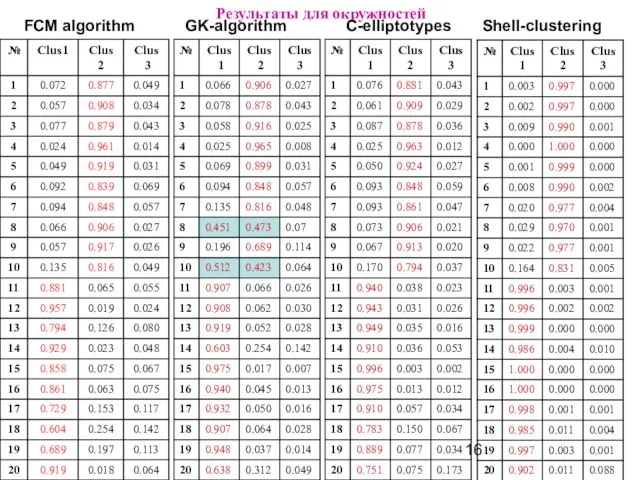
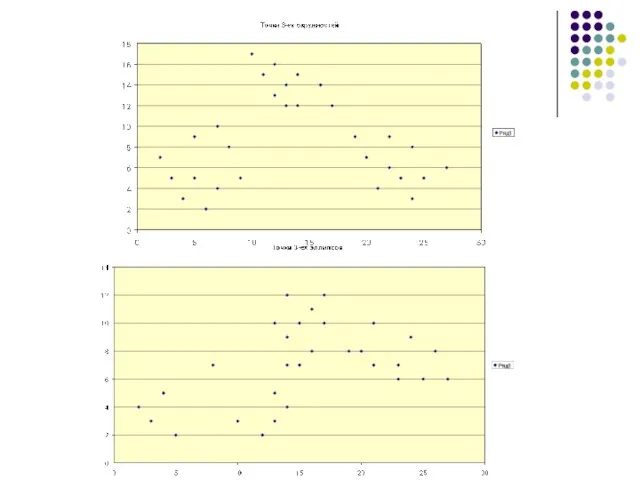
Слайд 17Результаты для окружностей
FCM algorithm
GK-algorithm
С-elliptotypes
Shell-clustering
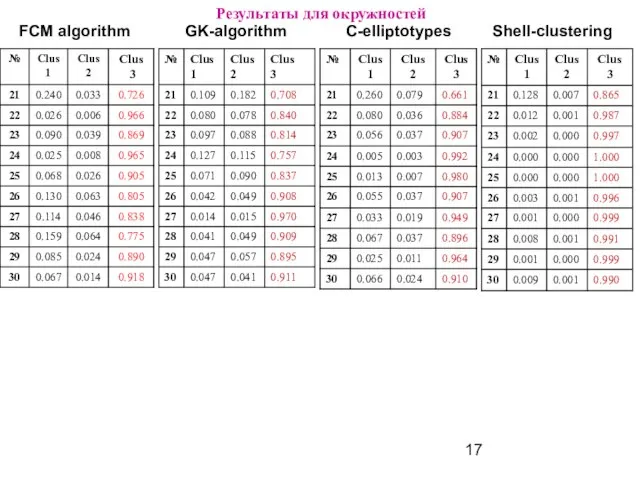
Слайд 18Результаты для эллипсов
FCM algorithm
GK-algorithm
С-elliptotypes
Shell-clustering
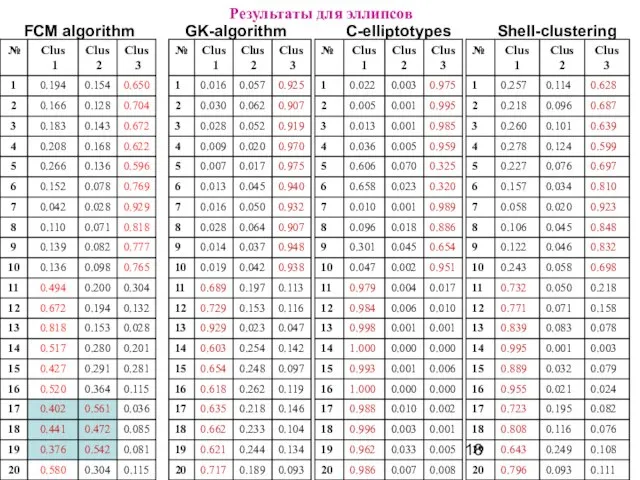
Слайд 19Результаты для эллипсов
FCM algorithm
GK-algorithm
С-elliptotypes
Shell-clustering
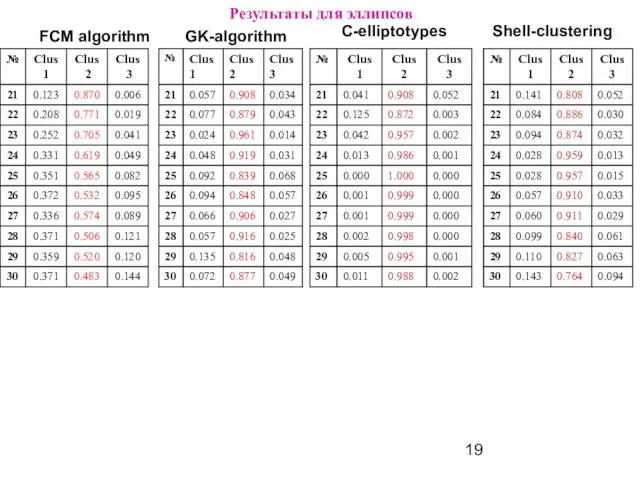
Слайд 20Библиографический список
1. Осовский С. Нейронные сети. М.: Финансы и статистика, 2002.
2. Сокал

Р.Р. Кластер-анализ и классификация: предпосылки и основные направления [Текст]/ Р.Р.Сокал. Под ред. Дж. Вэн Райзина. – М.:Мир, Классификация и кластер, 1980.
3. Bezdek J.C. Pattern recognition with fuzzy objective function algorithms. – Plenum Press, New York. – 1982.
4. Gustafson D.E., Kessel W.C. Fuzzy clustering with a fuzzy covariance matrix - http://www.egr.uh.edu/ece/faculty/karayiannis/Karayiannis_tnn_16(2)_05.pdf
5. Jain А. К. Data Clustering: A Review [Текст] / А. К. Jain, M. N. Murty, P. J. Flynn - http://www.csee.umbc.edu/nicholas/clustering/p264-jain.pdf, 2006.
6. Ahmed Ismail Shihab. Fuzzy clustering algorithmes and their application to medical image analysis, PhD dissertation, 2000.


















 Художественный мир и его компоненты
Художественный мир и его компоненты Оформление и дизайн
Оформление и дизайн prezentatsia_menedzhment (1)
prezentatsia_menedzhment (1) Презентация на тему Военные профессии в стихах и картинках
Презентация на тему Военные профессии в стихах и картинках Личность. Темперамент. Характер. Презентация
Личность. Темперамент. Характер. Презентация Ley de Propiedad Horizontal (LPH)
Ley de Propiedad Horizontal (LPH) Презентация на тему Повышение конкурентоспособности предприятия
Презентация на тему Повышение конкурентоспособности предприятия Как организовать школьный пресс-центр
Как организовать школьный пресс-центр Гондурас
Гондурас Тема 5. Международные морские перевозки грузов
Тема 5. Международные морские перевозки грузов Деньги их функции и виды
Деньги их функции и виды Жестокое обращение с ребенком
Жестокое обращение с ребенком РЕГУЛИРОВАНИЕ КАЧЕСТВА УСЛУГ В ОБЛАСТИ ЭЛЕКТРОЭНЕРГИИ В ИТАЛИИ
РЕГУЛИРОВАНИЕ КАЧЕСТВА УСЛУГ В ОБЛАСТИ ЭЛЕКТРОЭНЕРГИИ В ИТАЛИИ DER VOGEL
DER VOGEL 20.02.2012 года в старшей группе»Смородинка» прошел конкурс «Все дело в шляпе!»
20.02.2012 года в старшей группе»Смородинка» прошел конкурс «Все дело в шляпе!» Экономическое устройство России
Экономическое устройство России «Спасибо за жизнь!»
«Спасибо за жизнь!» Презентация на тему Петровские реформы
Презентация на тему Петровские реформы Эмпирическая методология. Научный метод и исследовательское мышление
Эмпирическая методология. Научный метод и исследовательское мышление О РАЗРАБОТКЕ СТАНДАРТОВ, ОБЕСПЕЧИВАЮЩИХ РЕАЛИЗАЦИЮ ПОСТАНОВЛЕНИЯ ПРАВИТЕЛЬСТВА РФ ОТ 31 ДЕКАБРЯ 2009 Г. № 1222
О РАЗРАБОТКЕ СТАНДАРТОВ, ОБЕСПЕЧИВАЮЩИХ РЕАЛИЗАЦИЮ ПОСТАНОВЛЕНИЯ ПРАВИТЕЛЬСТВА РФ ОТ 31 ДЕКАБРЯ 2009 Г. № 1222 Ведущая свадебных церемоний. Свадебная ведущая
Ведущая свадебных церемоний. Свадебная ведущая Как животные готовятся к зиме?
Как животные готовятся к зиме? Судебное разбирательство в первой инстанции
Судебное разбирательство в первой инстанции Показатели развития общей моторики малыша
Показатели развития общей моторики малыша Улица Панфилова
Улица Панфилова Киномания. Блиц
Киномания. Блиц Электронный университет КГЭУ - виртуальная образовательная среда
Электронный университет КГЭУ - виртуальная образовательная среда Семейство кошачьих
Семейство кошачьих