Кодирование информации (часть 1)

Представление чисел в ЭВМ

Формы представления чисел
В зависимости от того, как в ЭВМ представляется порядок Рх, различают 2 формы представления чисел:
представление числа в форме
с фиксированной запятой (или точкой) (ФФЗ или ФФТ);
представление числа в форме
с плавающей запятой (или точкой) (ФПЗ или ФПТ).

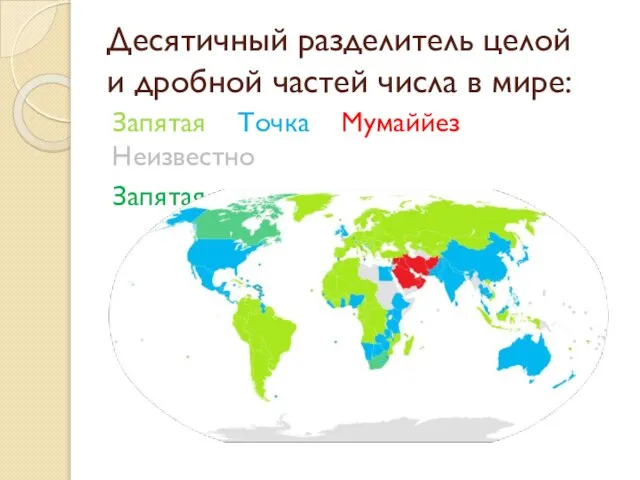
Десятичный разделитель целой
и дробной частей числа в мире:
Запятая Точка Мумаййез Неизвестно
Запятая и точка

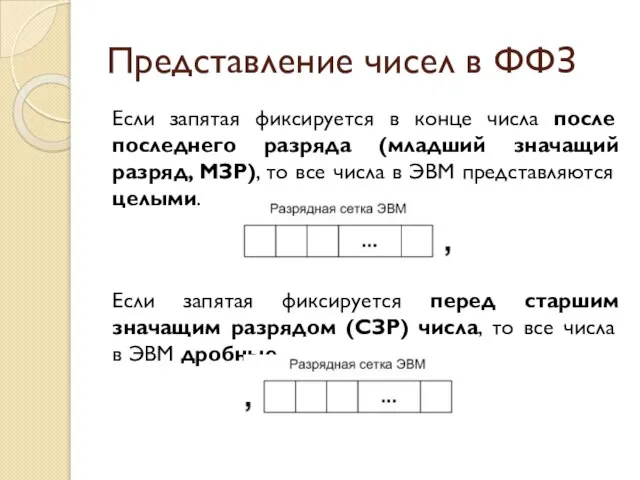
Представление чисел в ФФЗ
Если запятая фиксируется в конце числа после последнего разряда (младший значащий разряд, МЗР), то все числа в ЭВМ представляются целыми.
Если запятая фиксируется перед старшим значащим разрядом (СЗР) числа, то все числа
в ЭВМ дробные.

Диапазон представимых чисел
n
n

Переполнение разрядной сетки и машинный нуль
Числа, выходящие за правую границу диапазона, не могут быть представлены
в ЭВМ. Говорят, что произошло переполнение разрядной сетки ЭВМ.
Числа, выходящие за левую границу диапазона, представляются машинным нулем. Говорят, что произошла потеря значимости (антипереполнение).
Таким образом диапазон представимых
в ЭВМ чисел зависит от длины разрядной сетки ЭВМ.

Ошибка представления чисел

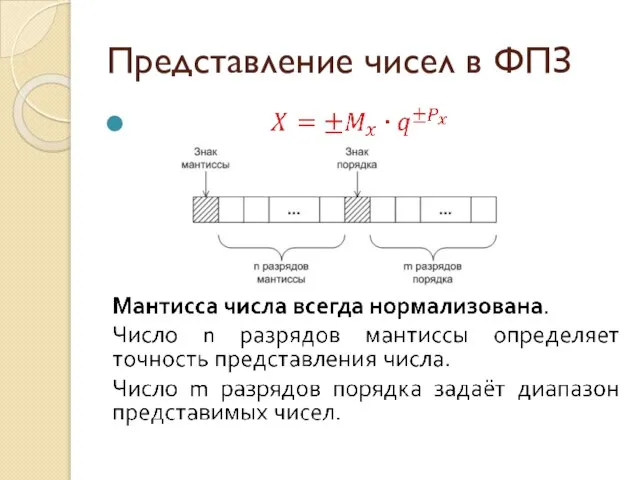
Представление чисел в ФПЗ

Диапазон представимых чисел
n
m
m

Ошибка представления мантиссы

Точность представления чисел и точность вычислений
Следует отличать точность предста-вления чисел от точности вычислений.
Точность вычислений зависит от чисел верных знаков в исходных данных
и от метода вычислений.
Отметим, что при работе с числами
в ФФЗ при длительных вычислениях происходит накопление ошибки, чего нет при работе с числами в ФПЗ.

Стандарт IEEE 754-2008
Стандарт описывает:
Формат ЧПЗ: мантисса, порядок, знак числа;
Представление «+0», «–0», «+∞», «–∞», NaN
(Not-a-Number, нечисло);
Исключительные ситуации: деление на нуль, переполнение, потерю значимости, работу
с денормализованными числами;
Методы для преобразования числа при выполнении математических операций;
Операции арифметические и др.

Используемые в ЭВМ форматы ЧПЗ
Стандарт IEEE 754-2008 определяет
5 основных форматов ЧПЗ:
Двоичные:
Одинарной точности (binary32);
Двойной точности (binary64);
Четверной точности (binary128).
Десятичные:
Decimal64;
Decimal128.

Сводная таблица основных форматов ЧПЗ
Наиболее употребляемыми форматами ЧПЗ являются форматы одинарной (binary32) и двойной (binary64) точности.
* – целая часть мантиссы; она всегда есть и равна 1, и поэтому её разряд не включается в состав формата в явном виде.

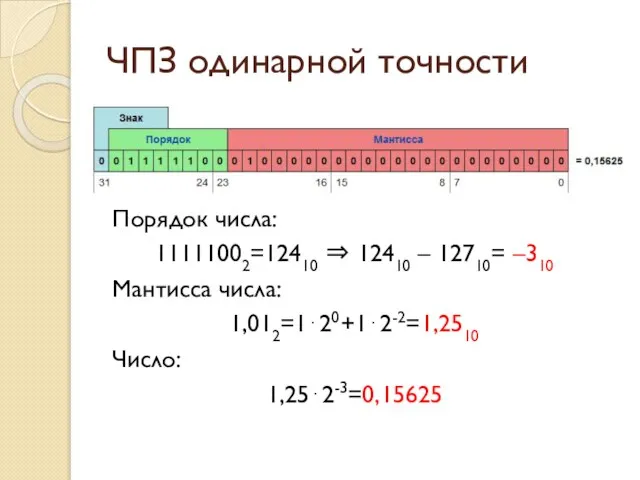
ЧПЗ одинарной точности
Порядок числа:
11111002=12410 ⇒ 12410 – 12710= –310
Мантисса числа:
1,012=1⋅20+1⋅2-2=1,2510
Число:
1,25⋅2-3=0,15625

ЧПЗ двойной точности
Например, если число:
0100000001011110110111010010111100011010100111111011111001110111
Порядок:
100000001012=102910 ⇒ 102910 – 102310 = 610
Мантисса:
1,11101101110100101111000110101001111110111110011101112=1,92910
Число:
1,929⋅26=123,456

ЧПЗ формат Decimal64
DPD – Densely Packed Decimal (плотно упакованная десятичная дробь)

Представление числа

Прямой код числа
k
n
m
k
n
m
k
n+m
k
n+m

Применение, достоинство и недостатки прямого кода
Прямые коды применяются в устройствах ввода/вывода и в запоминающих устройствах.
Достоинство прямого кода – удобство представления чисел.
Недостатки прямого кода:
Необходимо различать знаковые и числовые разряды, так как они по разному участвуют
в арифметических операциях.
Операции «+» и «–» производятся по разным алгоритмам.
2 представления числа нуль.

Обратный (инверсный) код числа
k
n
m
k
n
m
k
n+m
k
n+m

Выполнение операций в обратном коде
При алгебраическом сложении чисел
в обратных кодах знаковые разряды числа участвуют в операции наравне
с цифровыми. Если возникает перенос из старшего знакового разряда, то он суммируется к младшему цифровому разряду.

Дополнительный код
k
n
m
k
n
m

Выполнение операций в дополнительном коде
При алгебраическом сложении
в дополнительном коде знаковые
и цифровые разряды числа участвуют одинаково. Если возникает перенос
из старшего знакового разряда, то он отбрасывается.

Модифицированные коды
Рассмотренные коды позволяют выполнять операции «+» и «–»
по единому алгоритму, как операцию сложения. При этом не требуется разделение числа на знаковые
и цифровые разряды.
Если число разрядов, отводимое
под знак числа, >1, то коды называются модифицированными.

Переполнение разрядной сетки ЭВМ
В ЭВМ для записи машинного слова отводится определенное число разрядов, называемое длиной разрядной сетки.
При сложении чисел одного знака возможно появление результата, превышающего длину разрядной сетки. При этом старшая цифра числа попадает
в знаковый разряд.
Использование модифицированных кодов позволяет сохранить знак результата.

Признак переполнения разрядной сетки ЭВМ
Неодинаковое содержимое старшего знакового разряда, сохраняющего знак результата, и младшего знакового разряда, содержащего вышедшую за разрядную сетку цифру, служит признаком переполнения разрядной сетки ЭВМ.
С целью экономии оборудования
в большинстве ЭВМ принято отводить
под знак числа k=2 разряда.
При этом старший разряд называется знаковым, а младший – разрядом переполнения.

Ситуации при выполнении вычислений

Пример
Инверсный код
410+(-210)=210
410=001002
-210=111012
210=000102
1 1
+ 00 100
11 101
+ 1 00 001
1
00 010
Дополнительный код
410+(-210)=210
410=001002
-210=111102
210=000102
1 1
+ 00 100
11 110
1 00 010
Знак «+»
Разряды равны, значит переполнения нет

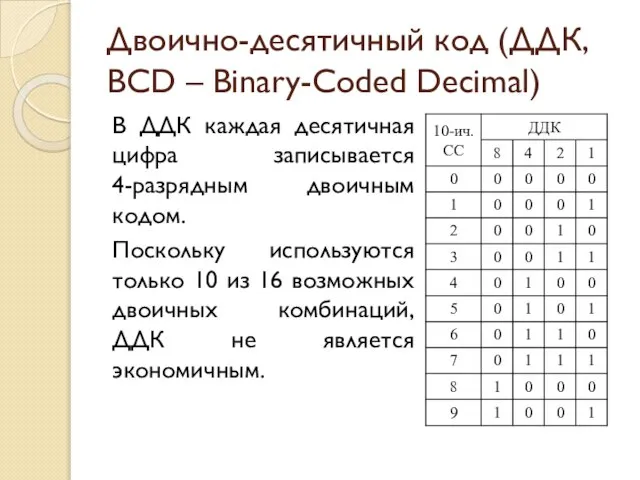
Двоично-десятичный код (ДДК, BCD – Binary-Coded Decimal)
В ДДК каждая десятичная цифра записывается 4-разрядным двоичным кодом.
Поскольку используются только 10 из 16 возможных двоичных комбинаций, ДДК не является экономичным.

Преимущества и недостатки ДДК
Преимущества:
Упрощенный вывод на индикацию;
Для дробных чисел не теряется точность при переводе в десятичный формат
и наоборот;
Упрощенные операции «*» и «/» на 10
и округление.
Недостатки:
Повышенный расход ресурсов памяти;
Усложнены операции «+» и «–».

Код Грея
Код Грея – такой код, каждое следующее значение кото-рого получается из предыду-щего изменением только одного разряда.
Имеет повышенную помехо-защищенность. Используется в датчиках-энкодерах.
1887 – 1969
Диск кругового
4-разрядного энкодера

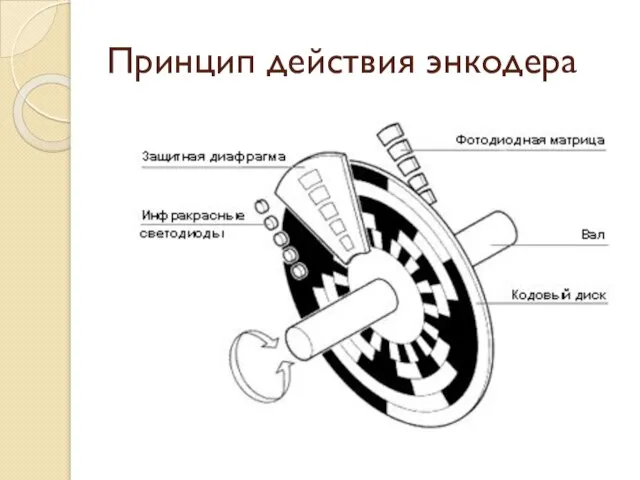
Принцип действия энкодера

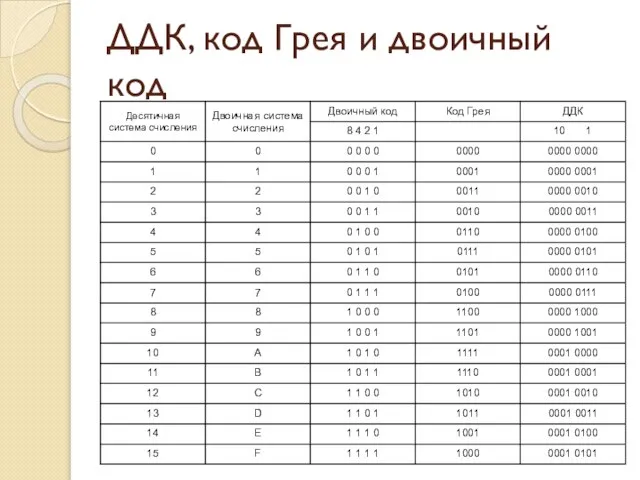
ДДК, код Грея и двоичный код

Приложение А. Нечисло (1)
Нечисло (англ. Not-a-Number, NaN) – особое состояние ЧПЗ. Может возникнуть, например, когда математическая операция завершилась с неопределённым резуль-татом, или если в ячейку памяти попало неудовлетворяющее условию число.
NaN бывает «тихий» и «сигнальный». Последний вызывает исключение, тогда как первый лишь возвращает NaN в каче-стве результата операции.

Приложение А. Нечисло (2)