Содержание
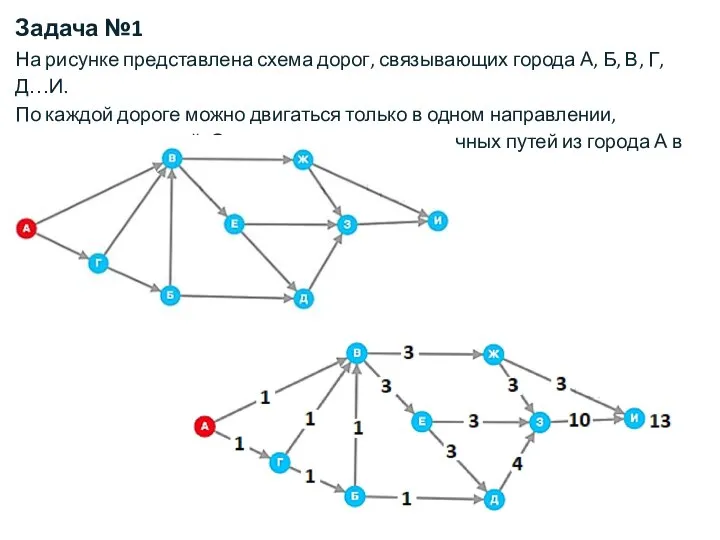
- 2. Задача №1 На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д…И. По каждой
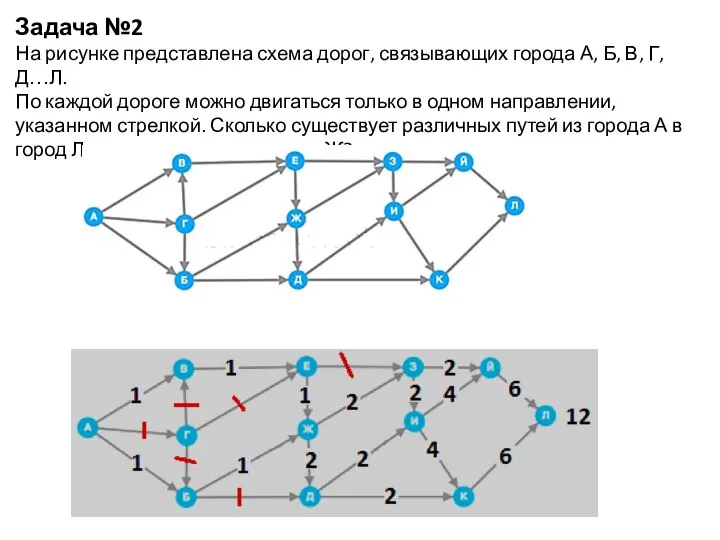
- 3. Задача №2 На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д…Л. По каждой
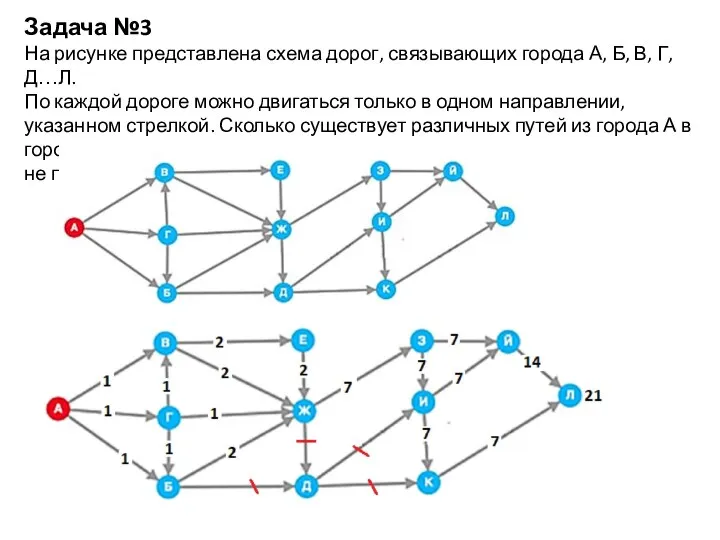
- 4. Задача №3 На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д…Л. По каждой
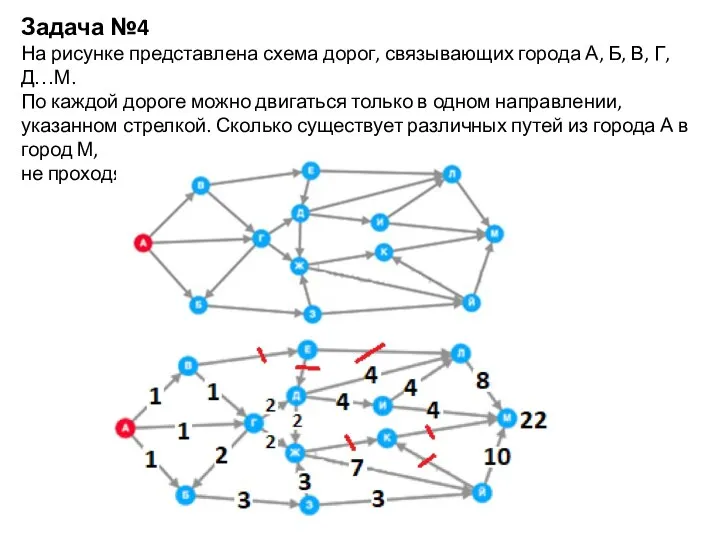
- 5. Задача №4 На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д…М. По каждой
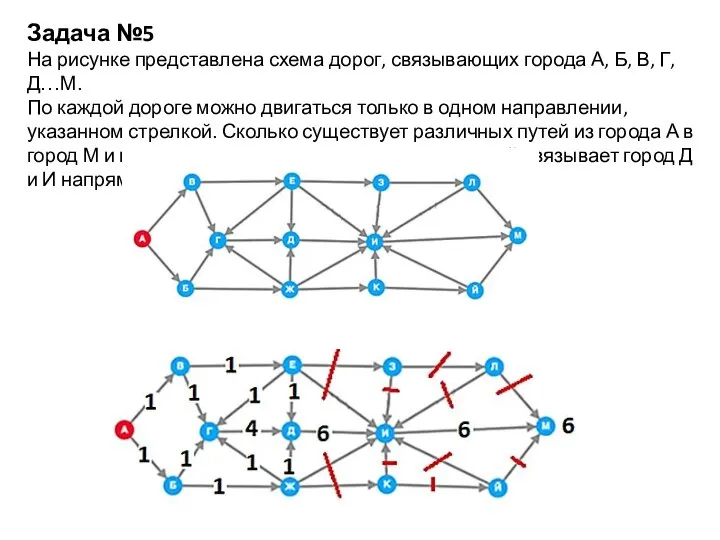
- 6. Задача №5 На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д…М. По каждой
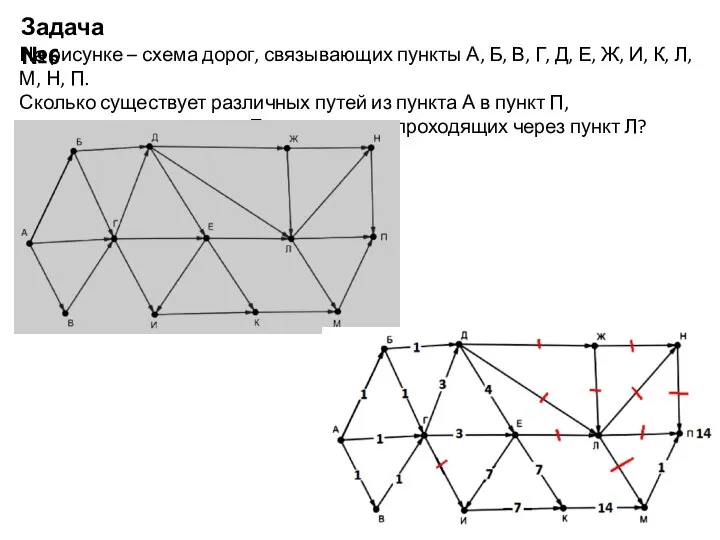
- 7. На рисунке – схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К,
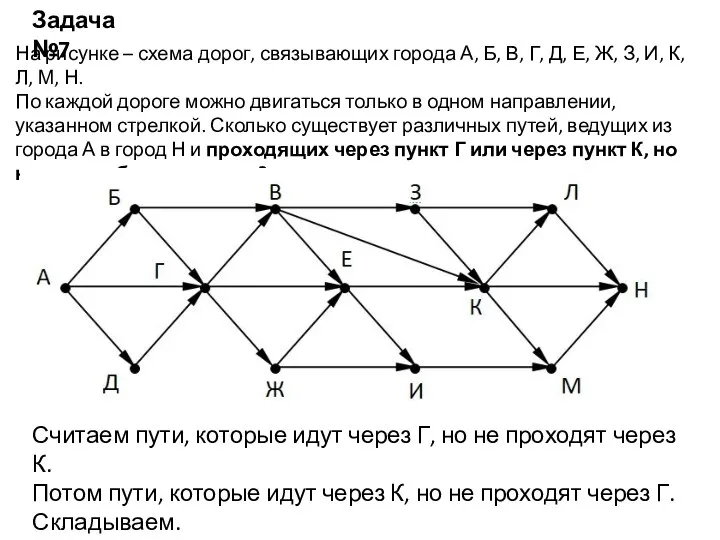
- 8. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И,
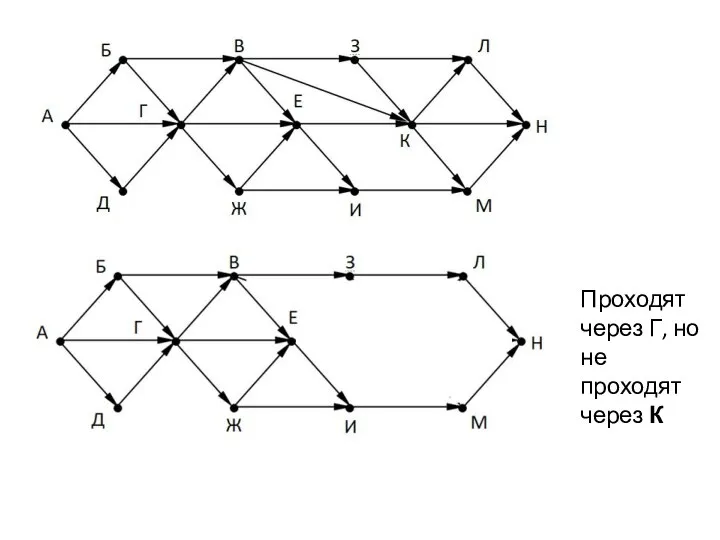
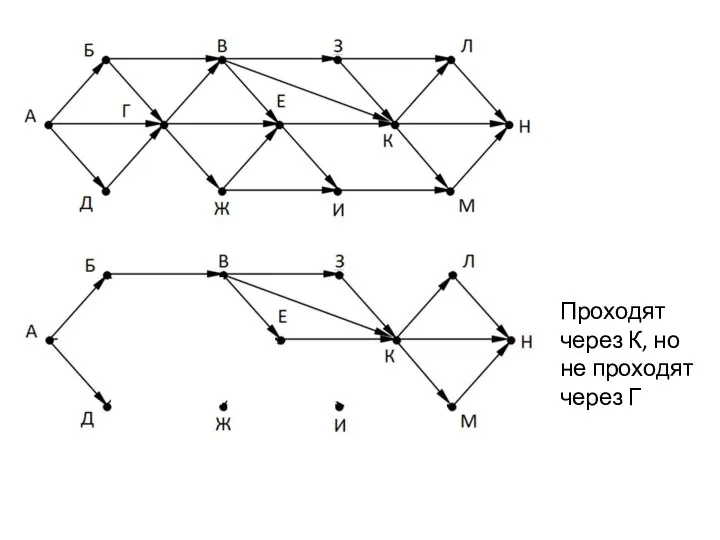
- 9. Проходят через Г, но не проходят через К
- 10. Проходят через К, но не проходят через Г
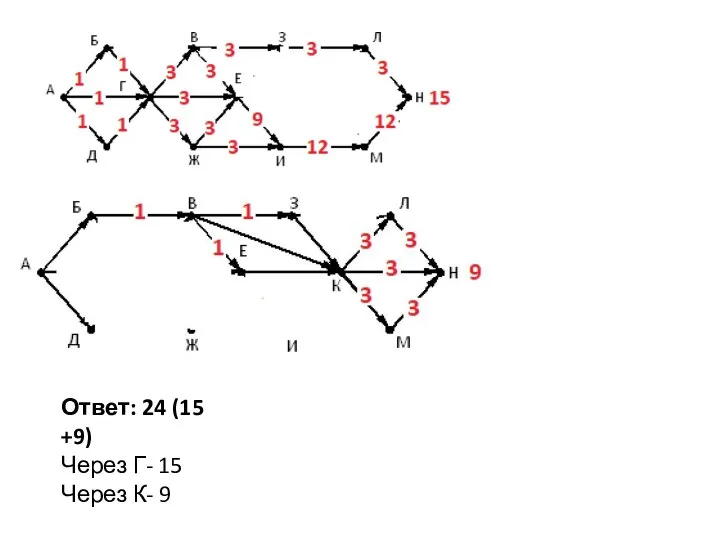
- 11. Ответ: 24 (15 +9) Через Г- 15 Через К- 9
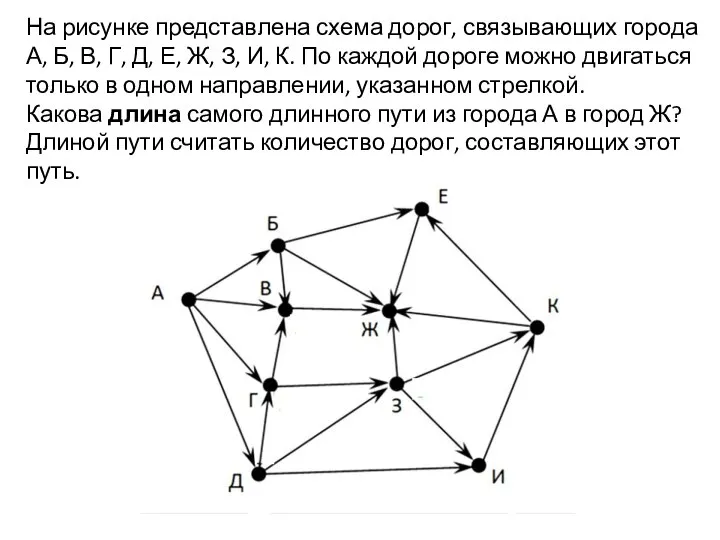
- 12. Длина самого длинного пути.
- 13. На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И,
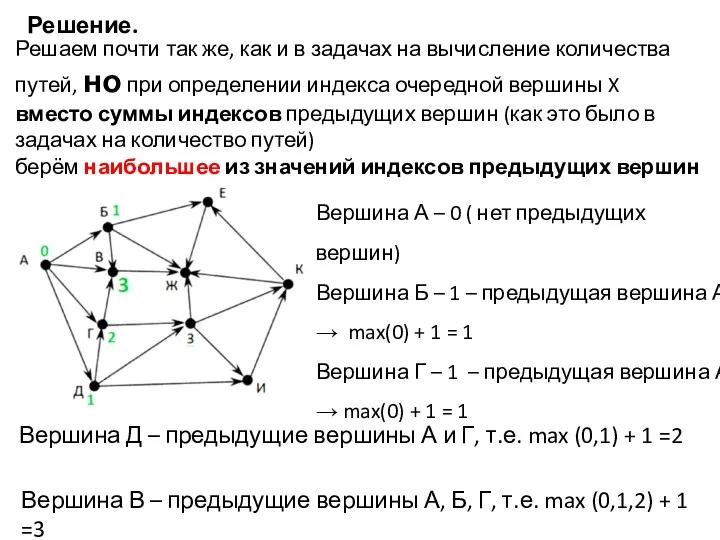
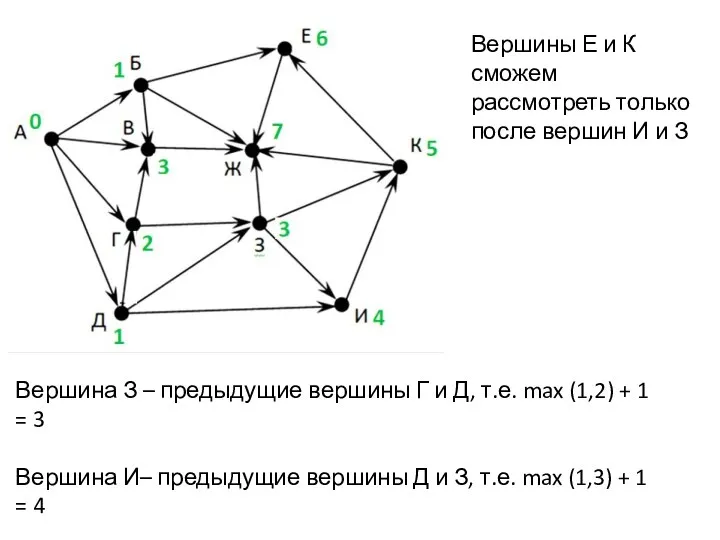
- 14. Решение. Решаем почти так же, как и в задачах на вычисление количества путей, но при определении
- 15. Вершины Е и К сможем рассмотреть только после вершин И и З Вершина З – предыдущие
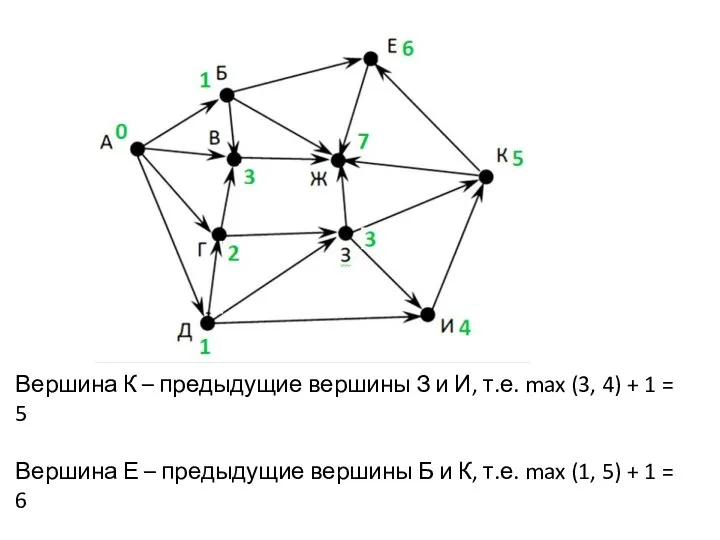
- 16. Вершина К – предыдущие вершины З и И, т.е. max (3, 4) + 1 = 5
- 18. Скачать презентацию

 School
School Снежинка
Снежинка Модель Айсберг управления изменениями (Ф.Кругер)
Модель Айсберг управления изменениями (Ф.Кругер) Методика обучения
Методика обучения Игра «Умники и Умницы»
Игра «Умники и Умницы» Подведение итогов ежегодного городского конкурса Самый благоустроенный район города Красноярска 2018 год
Подведение итогов ежегодного городского конкурса Самый благоустроенный район города Красноярска 2018 год СОВРЕМЕННЫЕ ТЕНДЕНЦИИ В УПРАВЛЕНИИ АКТИВАМИ ПЕНСИОННЫХ ФОНДОВ
СОВРЕМЕННЫЕ ТЕНДЕНЦИИ В УПРАВЛЕНИИ АКТИВАМИ ПЕНСИОННЫХ ФОНДОВ Сатирический портрет в искусстве
Сатирический портрет в искусстве Методика цветовых метафор
Методика цветовых метафор Презентация на тему Гуляй по улицам с умом
Презентация на тему Гуляй по улицам с умом 115 лет Сергею Есенину
115 лет Сергею Есенину Гипноз и самогипноз в спорте. От мысли к действиям
Гипноз и самогипноз в спорте. От мысли к действиям Аккумуляторная батарея премиум-класса
Аккумуляторная батарея премиум-класса Превратим Васюки в Нью-Москву
Превратим Васюки в Нью-Москву Транспорт и сфера услуг
Транспорт и сфера услуг  Общероссийский классификатор продукции по видам экономической деятельности (ОКПД)
Общероссийский классификатор продукции по видам экономической деятельности (ОКПД) Проекции плоскости. Лекция 3
Проекции плоскости. Лекция 3 Сочинение–повествование по картине В.М. Васнецова Иван Царевич на Сером волке
Сочинение–повествование по картине В.М. Васнецова Иван Царевич на Сером волке Понятие культуры (1)
Понятие культуры (1) Фотографии
Фотографии Строевые упражнения
Строевые упражнения Эмоции, эмоциональные состояния и чувства
Эмоции, эмоциональные состояния и чувства Презентация на тему Ковровые изделия
Презентация на тему Ковровые изделия  Web 2.0 проект в период кризиса
Web 2.0 проект в период кризиса Презентация Э-20-3
Презентация Э-20-3 Адмирал Ушаков
Адмирал Ушаков «Планирование склада запасных частей»
«Планирование склада запасных частей» Презентация на тему Кто ты Русь
Презентация на тему Кто ты Русь