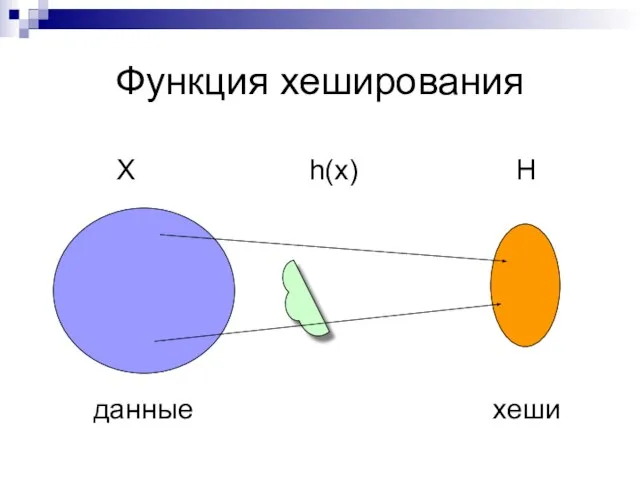
Слайд 2Функция хеширования
X h(x) H
данные хеши
Слайд 3Функция хеширования
Свойства:
Необратимость
Стойкость к коллизиям
Слабая
Сильная
Применение в криптографии
ЭЦП, пароли и т.д.

Слайд 4Алгоритм Меркла-Дамгарда
1 2 . . . N pad
IV h h
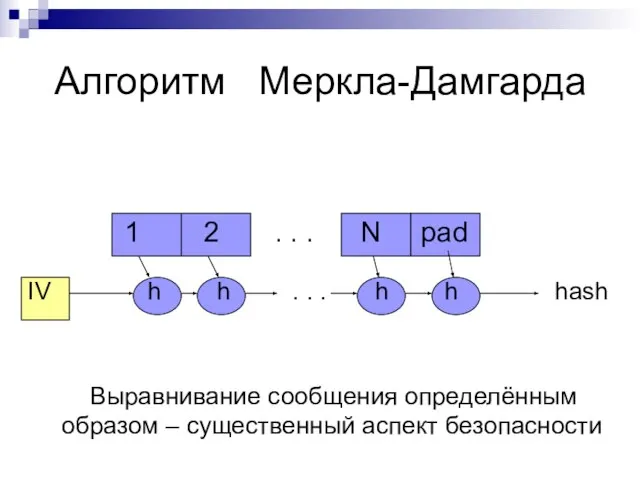
. . . h h hash
Выравнивание сообщения определённым образом – существенный аспект безопасности
Слайд 5Коллизии хеш-функций
Практически любая хеш-функция имеет коллизии
В хороших х.ф. коллизии крайне редки
«Идеальная х.ф.»

- если заранее известны все значения входных данных
Слайд 7Типы атак на хеш-функции
Для n-битной хеш-функции
Атака на обнаружение коллизий
Требует ~

2n/2 операций (парадокс дней рождения)
Атака на нахождение прообраза
Требует ~ 2n операций
Слайд 8MD5
Доббертин (1996г)
Псевдоколлизия – использовал свои IV
Если MD5(x) = MD5(y), то MD5(x||S) =

MD5(y||S)
Ванг и Ю
Мощный метод нахождения коллизий, основанный на дифференциальной атаке. ~ 240 операций
Были приведены некоторые коллизии и написана программа для генерирования архивов и документов PDF с одинаковыми хешами
Слайд 9SHA-0
Ванг
Атака методом дифференциальных путей
Используется возможность создания локальных коллизий в SHA-0
Сложность «прямой»

реализации ~ 242 операций
Можно заранее составить таблицу подходящих сообщений, тогда сложность составляет ~ 239 операций
Слайд 10SHA-1
Ванг, Йинг, Ю
Расширимые сообщения – разновидность множественной коллизии.
Атака с использованием очень длинных

сообщений
Находят все промежуточные хеши для очень длинного сообщения и перебирают около 2106 блоков до совпадения с одним из исходных. Находят расширимое сообщение и расширяют его до длины исходного. Получают второй прообраз.
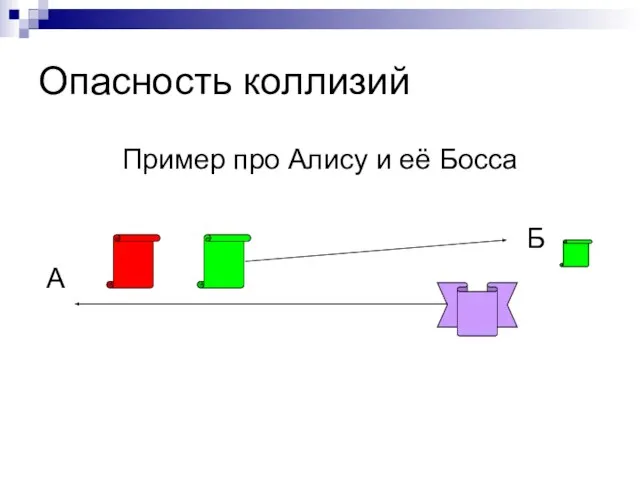
Слайд 11Опасность коллизий
Пример про Алису и её Босса
Б
А
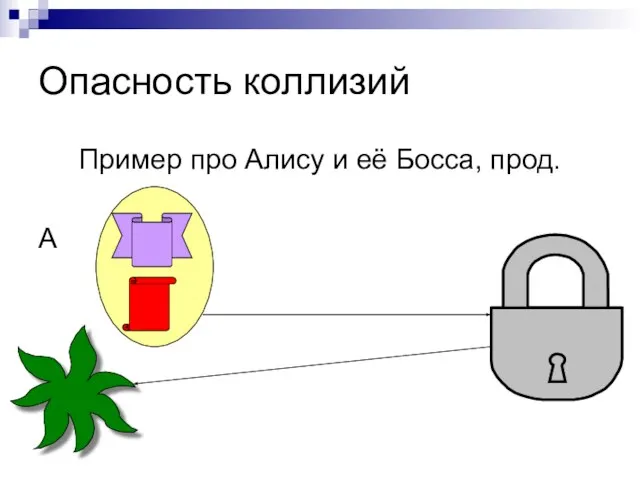
Слайд 12Опасность коллизий
Пример про Алису и её Босса, прод.
А










 Реализация проекта «Лицейский технопарк» в рамках программы развития «МПЛ как инновационный образовательный центр».
Реализация проекта «Лицейский технопарк» в рамках программы развития «МПЛ как инновационный образовательный центр». Разработка стратегии развития предприятия сферы услуг
Разработка стратегии развития предприятия сферы услуг Жизнь в профессии Имидж учителя
Жизнь в профессии Имидж учителя Системы управления качеством
Системы управления качеством Подсистема памяти МПС
Подсистема памяти МПС Удержание ключевых сотрудников
Удержание ключевых сотрудников Информационная война. Распространение ложной информации
Информационная война. Распространение ложной информации Презентация на тему Мещерский край в географии и литературе
Презентация на тему Мещерский край в географии и литературе  Политика. Представления о политике. Политика как подсистема общества
Политика. Представления о политике. Политика как подсистема общества ОАО МРСК «Центра и Северного Кавказа»
ОАО МРСК «Центра и Северного Кавказа» Общие условия досудебного производства
Общие условия досудебного производства Некоммерческая организация «Ассоциация московских вузов»МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИРОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ АГЕ
Некоммерческая организация «Ассоциация московских вузов»МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИРОССИЙСКОЙ ФЕДЕРАЦИИФЕДЕРАЛЬНОЕ АГЕ Понедельник - день тяжелый?
Понедельник - день тяжелый? Управление воспитательным процессом
Управление воспитательным процессом Event менеджмент
Event менеджмент Космические аппараты на марках сразных стран
Космические аппараты на марках сразных стран Презентация на тему ЦАРСТВО ПРОКАРИОТЫ ПОДЦАРСТВО БАКТЕРИИ
Презентация на тему ЦАРСТВО ПРОКАРИОТЫ ПОДЦАРСТВО БАКТЕРИИ  Химия в криминалистике
Химия в криминалистике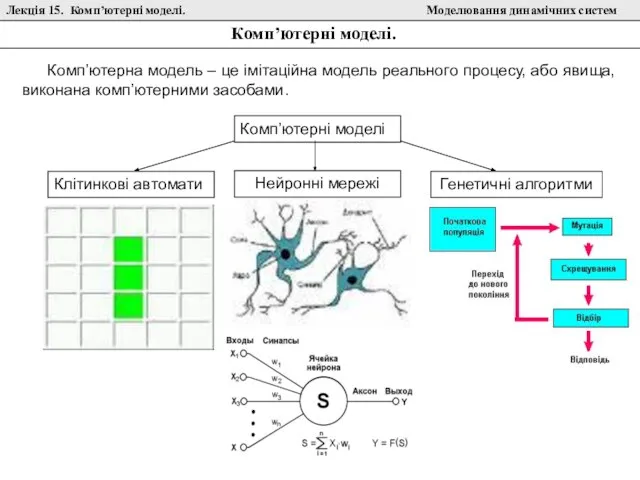 Клітинкові автомати
Клітинкові автомати Числовой луч (2 класс)
Числовой луч (2 класс) Адресаты лирики А.С. Пушкина.Женские портреты.
Адресаты лирики А.С. Пушкина.Женские портреты. Тема проекта:«Спортивные игры»
Тема проекта:«Спортивные игры» Проектирование информационных систем
Проектирование информационных систем Мое мировоззрение. Мое отношение к религии
Мое мировоззрение. Мое отношение к религии НОВЫЕ ТЕХНОЛОГИИ на рынке ГКО-ОФЗ на ММВБ
НОВЫЕ ТЕХНОЛОГИИ на рынке ГКО-ОФЗ на ММВБ 14 марта – День православной книги
14 марта – День православной книги Інформаційна система та її складові
Інформаційна система та її складові Доклад«Теоретические аспекты информационного поиска»
Доклад«Теоретические аспекты информационного поиска»