Комбинаторика. Часть 1

2
раздел математики,
в котором изучаются вопросы о том сколько различных комбинаций подчиненных тем или иным условиям можно составить из заданных объектов.
Комбинаторика

3
Правило произведения

4
Задача №1 : В магазине «Всё для чая» есть пять разных чашек и три разных блюдца. Сколькими способами можно купить чашку с блюдцем?
Решение:
Чашку ( A) можно выбрать 5-ю (m) способами, а блюдце (B) - 3 –мя (n).
Значит, чашку с блюдцем можно выбрать: 5 х 3 = 15 способами.
Правило

5
Задача №2 : Пусть в этом же магазине продается ещё четыре разные чайные ложки. Каково количество способов купить комплект из чашки, блюдца и ложки?
Решение:
Чашку можно выбрать 5-ю способами,
а блюдце - 3 –мя, чайную ложку 4-мя .
Значит, чашку с блюдцем и ложку можно выбрать: 5 х 3 х 4 = 60 способами.
Правило

6
Задача №3: Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
Решение: В таких числах последняя цифра будет такая же, как и первая, а предпоследняя - как и вторая. Третья цифра будет любой. Это число можно представить в виде YZXZY , где X и Z- любые цифры, а Y- не ноль, т.е. X=Z=10 ; Y=9. Значит по правилу произведения количество чисел одинаково читающихся как слева направо, так и справа налево равно 9*10*10=900 вариантов.
Правило

7
Правило суммы
Если элемент A можно выбрать m различными способами, а независимый элемент B можно выбрать n различными способами, то выбрать A или B можно m+n способами.

8
Задача №4:
На блюдце лежат 7 яблок и 8 груш. Каким количеством способов можно выбрать один плод.
Решение:
Одно яблоко (A) можно
выбрать 7-ю (m) способами,
а одну грушу (B)
8-ю ( n) способами.
Один плод можно выбрать
7+8=15 способами.
Правило

9
Задача №5: Ученик должен выполнить практическую работу по математике. Ему предложили на выбор 17 тем по алгебре и 13 тем по геометрии. Сколькими способами он может выбрать одну тему для практической работы?
Решение:
Тему по алгебре (A) можно выбрать 17-ю (m) способами, а тему по геометрии (B) 13-ю
(n) способами. Одну тему для практической работы ученик может выбрать 17+13=30 способами.
Правило

10
Факториал
Произведение натуральных чисел от
1 до n в математике называют факториалом числа n и обозначают n!
В таблице представлены несколько значений факториала для возрастающих значений n

11
Перестановки
Перестановкой из n элементов называется комбинация, в которой все эти n элементов расположены в определенном порядке.
Перестановки отличаются друг от друга только порядком расположения элементов.
n = 3

12
Задача №6 : назовите треугольник ABC всеми возможными способами:
Задача №7 : сколькими способами можно расставить на книжной полке собрание сочинений Диккенса, включающее 30 томов.
Формула

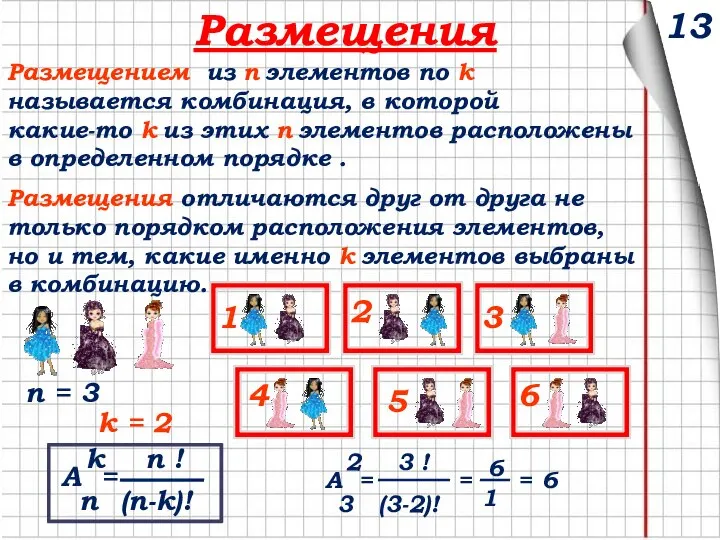
13
Размещения
Размещением из n элементов по k
называется комбинация, в которой
какие-то k из этих n элементов расположены в определенном порядке .
Размещения отличаются друг от друга не только порядком расположения элементов, но и тем, какие именно k элементов выбраны в комбинацию.

14
Задача №8 : назовите стороны треугольника ABC всеми возможными способами:
Ответ : АВ; ВА;
АС; СА; ВС; СВ
Задача №9 : на книжную полку влезает только 8 любых томов из 30-ти томного собрания Диккенса. Сколькими способами можно заполнить этими томами такую полку?
Формула

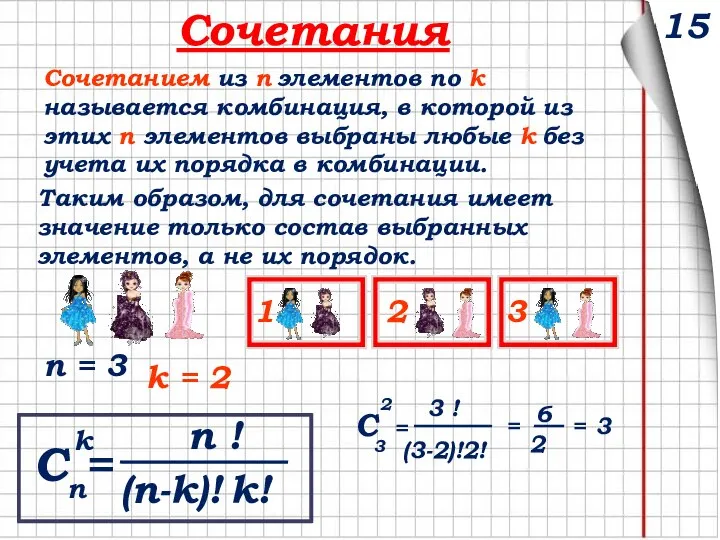
15
Сочетания
Сочетанием из n элементов по k называется комбинация, в которой из этих n элементов выбраны любые k без учета их порядка в комбинации.
Таким образом, для сочетания имеет значение только состав выбранных элементов, а не их порядок.

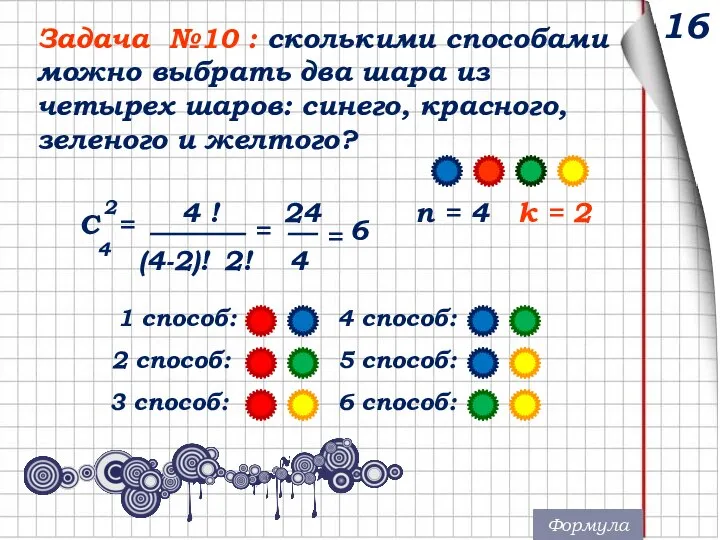
16
Задача №10 : сколькими способами можно выбрать два шара из четырех шаров: синего, красного, зеленого и желтого?
Формула

17
Различие между перестановками, размещениями, сочетаниями
В случае перестановок берутся все элементы и изменяется только их местоположение.
В случае размещений берётся только часть элементов и важно расположение элементов друг относительно друга.
В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.

18
раздел математики изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства
и операции над ними.
Событие называется случайным ,
если при одних и тех же условиях оно
может как произойти, так и не произойти.

19
В теории вероятностей случайные события могут быть, в том числе :
невозможные, которые никогда не смогут произойти;
достоверные, которые происходят при любом случае.
Например:
невозможное : на игральном кубике выпадет семь очков;
достоверное: на игральном кубике выпадет меньше семи очков.

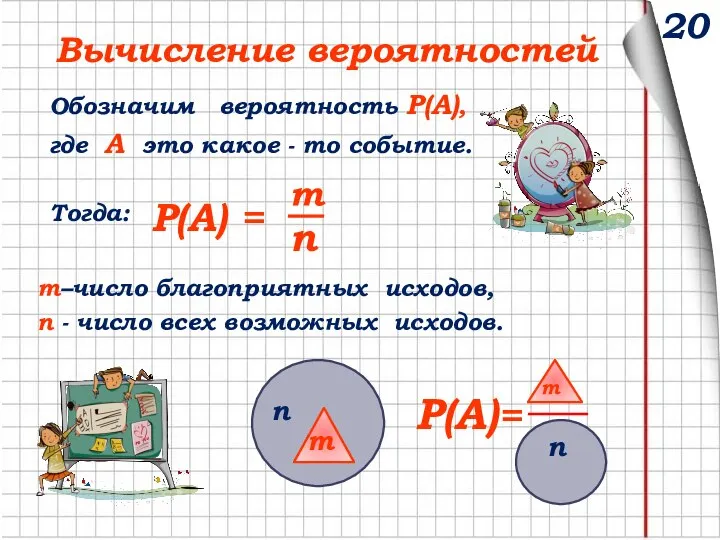
20
Вычисление вероятностей
Обозначим вероятность Р(А),
где А это какое - то событие.
Тогда:
m–число благоприятных исходов,
n - число всех возможных исходов.

21
Задача №11 : В коробке находятся 12 белых и 8 синих шаров. Какова вероятность того, что наудачу вынутый шар будет белым?
Решение:
n - число всех возможных (случаев) исходов;
m - число случаев, что будет вынут белый шар.
n = 12+8= 20 ; m =12
Тогда по формуле найдем вероятность вынуть белый шар :
Вероятность того, что наудачу вынутый шар будет белым будет равна :

22
Задача №12 : Из карточек составили слово «математика» . Какую карточку с буквой вероятнее всего вытащить? Какие события равновероятны?
Решение: Всего 10 букв.
Буква «м» встречается 2 раза : P(м) = 2/10;
буква «а» встречается 3 раза : P(а) = 3/10;
буква «т» встречается 2 раза : P(т) = 2/10;
буква «е» встречается 1 раз : P(е) = 1/10;
буква «и» встречается 1 раз : P(и) = 1/10;
буква «к» встречается 1 раз : P(к) = 1/10.

23
Ответ:
1. Вероятнее всего вытащить карточку с буквой «а»: P(а) = 3/10
2. Вероятность одинакова у букв «м», «т», : P(м/т) = 2/10.
3. Вероятность одинакова у букв «е», «к», «и»: P(е/к/и) = 1/10 .

24
Комбинаторика и теория вероятностей неразрывно связаны с нашей повседневной жизнью. Эти разделы изучения математики подготовят нас :
к выбору наилучшего из возможных вариантов;
оценке степени риска; шансу на успех;
позволяет судить о разумности ожидания наступления одних событий по сравнению с другими.
Теория вероятностей широко используется в теоретических и прикладных науках: физике, геодезии, теории автоматического управления и т.д. В частности, она служит теоретической базой математической и прикладной статистики, на основе которых осуществляется планирование и организация производства.