Содержание
- 2. Цели урока: - усвоить определение компланарных векторов; - рассмотреть признак компланарности трёх векторов; - рассмотреть правило
- 3. Определение Векторы называются компланарными, если при откладывании от одной и той же точки они будут лежать
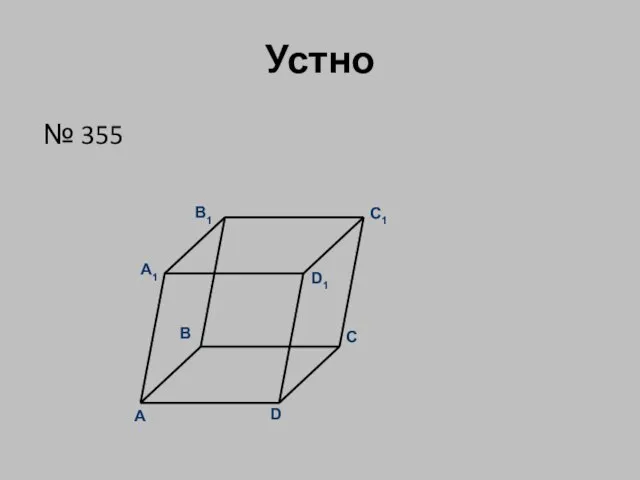
- 4. Устно № 355
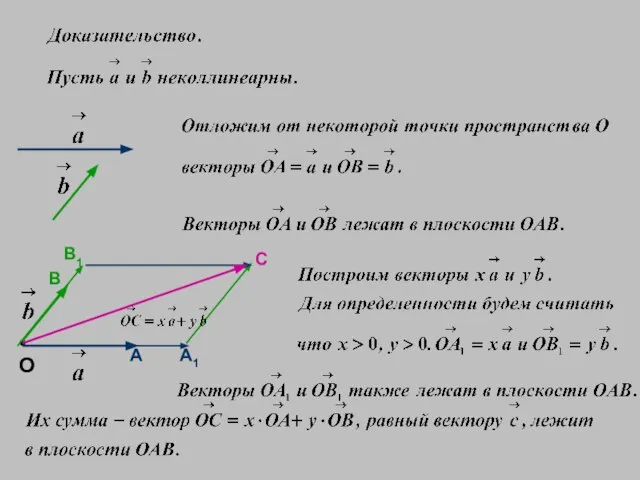
- 5. Признак компланарности трёх векторов
- 6. • О А1 В1 С
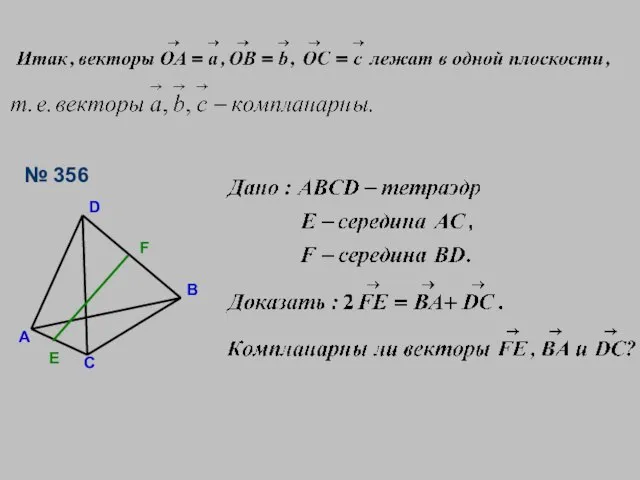
- 7. № 356
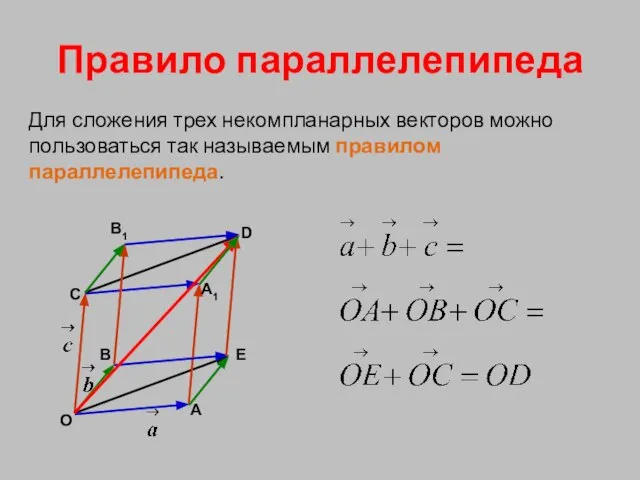
- 8. Правило параллелепипеда Для сложения трех некомпланарных векторов можно пользоваться так называемым правилом параллелепипеда. Е С В
- 9. Домашнее задание: п.39, 40 № 358
- 10. Тема урока: Разложение вектора по трем некомпланарным векторам.
- 11. Цели урока - изучить теорему о разложении вектора по трём некомпланарным векторам; - научиться применять полученные
- 12. Если вектор представлен в виде: где x, y, z – некоторые числа, то говорят, что вектор
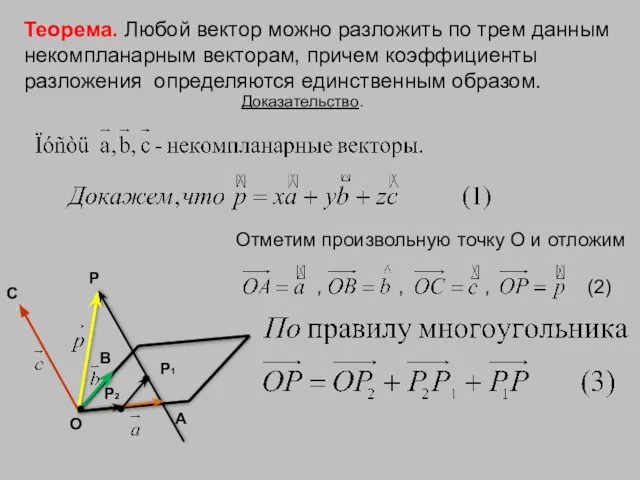
- 13. С В А О P Теорема. Любой вектор можно разложить по трем данным некомпланарным векторам, причем
- 14. Векторы коллинеарны, поэтому существуют числа х, у, z такие, что . С В А О P
- 16. Скачать презентацию








 Мой класс – мои друзья
Мой класс – мои друзья Дождь, или ода ангелу дождя Матариэлю. Нургисаева Айжана
Дождь, или ода ангелу дождя Матариэлю. Нургисаева Айжана Новые стандарты: опыт, результаты, проблемы
Новые стандарты: опыт, результаты, проблемы Презентация на тему Магическая цифра 7
Презентация на тему Магическая цифра 7 Berol 226
Berol 226 Внимание!
Внимание! Работа фотографа над проектом - создание визуального продукта, объединённого общей темой и стилистическим решением
Работа фотографа над проектом - создание визуального продукта, объединённого общей темой и стилистическим решением Прославившиеся ученые Саратовской области
Прославившиеся ученые Саратовской области ТЕСТ «Растениеводство. Защитники полей, садов и огородов»
ТЕСТ «Растениеводство. Защитники полей, садов и огородов» Мониторинг образовательных достижений учащихся 3 классов (на начало учебного года)
Мониторинг образовательных достижений учащихся 3 классов (на начало учебного года) Продвижение заведения на Gloss.ua
Продвижение заведения на Gloss.ua Цитрусовый АромаБранч
Цитрусовый АромаБранч Greek cuisine
Greek cuisine Информационно-справочные документы. Докладная записка
Информационно-справочные документы. Докладная записка Создание культурной среды при обучении младших школьников иностранному языку
Создание культурной среды при обучении младших школьников иностранному языку «Культурные фестивали в Санкт-Петербурге как пример внедрения творческих индустрий»
«Культурные фестивали в Санкт-Петербурге как пример внедрения творческих индустрий» СПЕЦИФИЧНОСТЬ ПАРАЗИТОВ
СПЕЦИФИЧНОСТЬ ПАРАЗИТОВ Биоритмы
Биоритмы Анализ технического состояния привода роликов отводящего рольганга электросталеплавильного цеха ПАО ММК
Анализ технического состояния привода роликов отводящего рольганга электросталеплавильного цеха ПАО ММК 天气
天气 КУЛИКОВСКАЯ БИТВА
КУЛИКОВСКАЯ БИТВА Camping
Camping Отто Кернберг о консультировании организаций
Отто Кернберг о консультировании организаций Санитарно-гигиенические требования к механической и термической обработке: Живой и солёной рыбы
Санитарно-гигиенические требования к механической и термической обработке: Живой и солёной рыбы Процессы разрушения и нагрузки на инструменты горных машин. ТИПИ. Тема 3
Процессы разрушения и нагрузки на инструменты горных машин. ТИПИ. Тема 3 Гаилә
Гаилә Исполнители вокруг нас. Разнообразие исполнителей
Исполнители вокруг нас. Разнообразие исполнителей Излучение и спектры
Излучение и спектры