Конус. Сечение конуса плоскостями

Конусом называется тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.

Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими конуса. Поверхность конуса состоит из основания и боковой поверхности.

Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания.

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса является прямая, содержащая её высоту .

Сечение конуса плоскостями. Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. Это сечение, которое проходит через ось конуса.

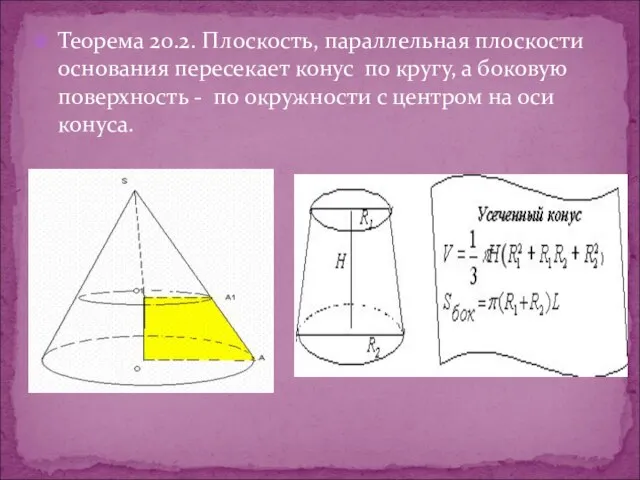
Теорема 20.2. Плоскость, параллельная плоскости основания пересекает конус по кругу, а боковую поверхность - по окружности с центром на оси конуса.

Плоскость , параллельная основанию конуса и пересекающая конус, отсекает от него меньший конус. Оставшаяся часть называется усечённым конусом.