Слайд 2Конусом называется тело, ограниченное кругом (основание конуса), и конической поверхностью, образованной отрезками,
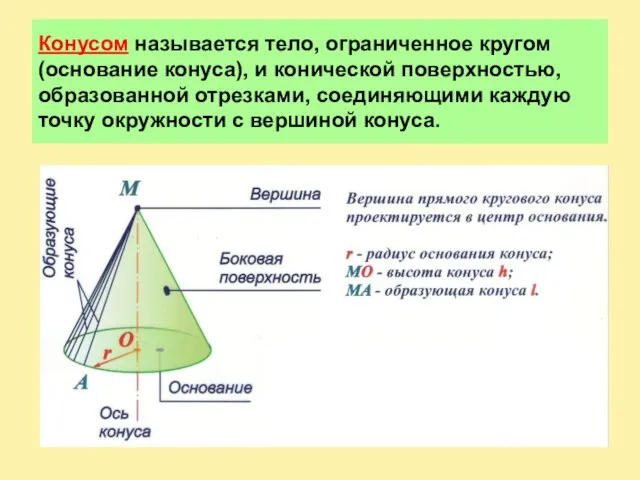
соединяющими каждую точку окружности с вершиной конуса.
Слайд 3Конус – тело вращения
Конус может быть получен вращением прямоугольного треугольника вокруг одного
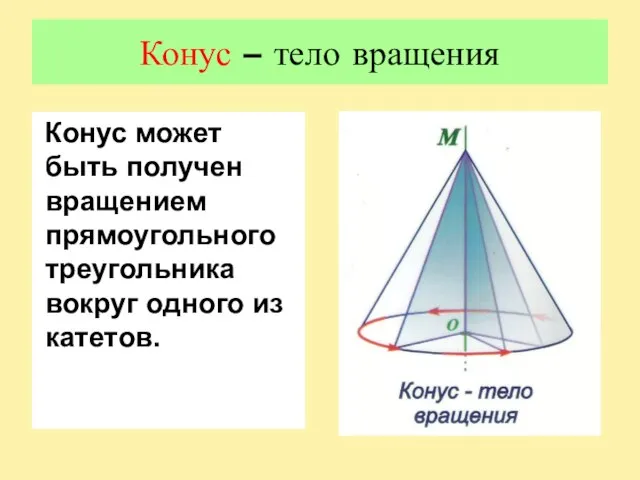
из катетов.
Слайд 4Боковая поверхность конуса – круговой сектор, радиус которого равен образующей конуса, а
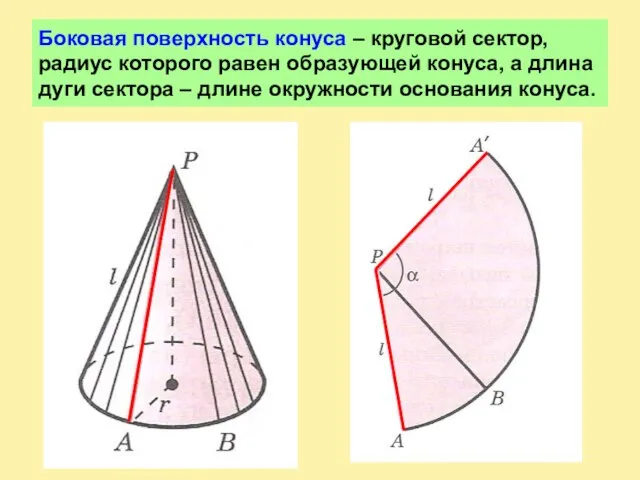
длина дуги сектора – длине окружности основания конуса.
Слайд 5Площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую:
Боковая
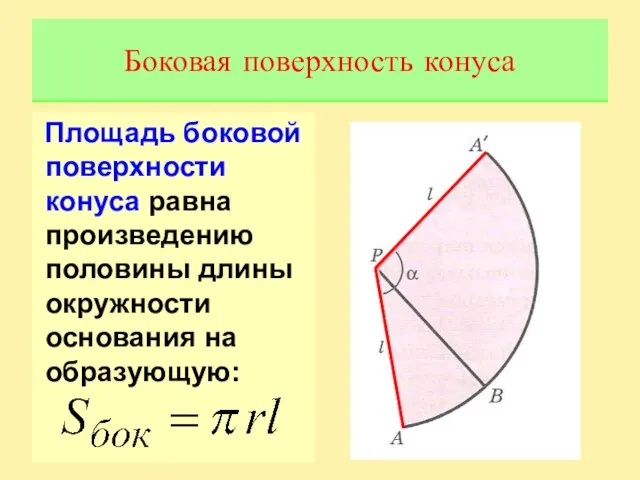
поверхность конуса
Слайд 6Площадь полной поверхности конуса равна сумме площадей боковой поверхности и основания:
Полная поверхность
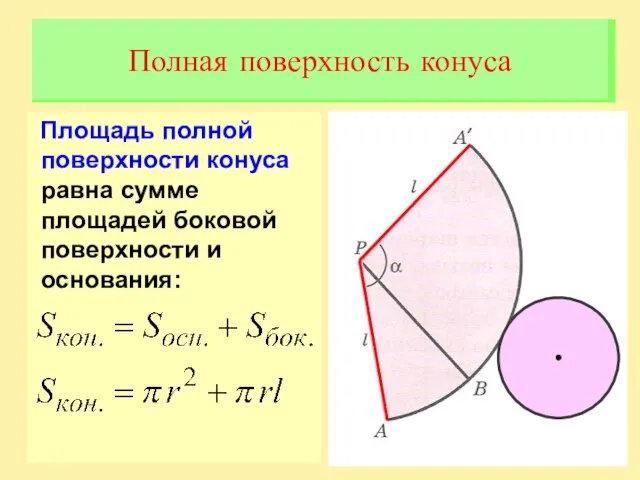
конуса
Слайд 7Задача 1. Высота конуса равна 12, а радиус основания равен 5. Найдите
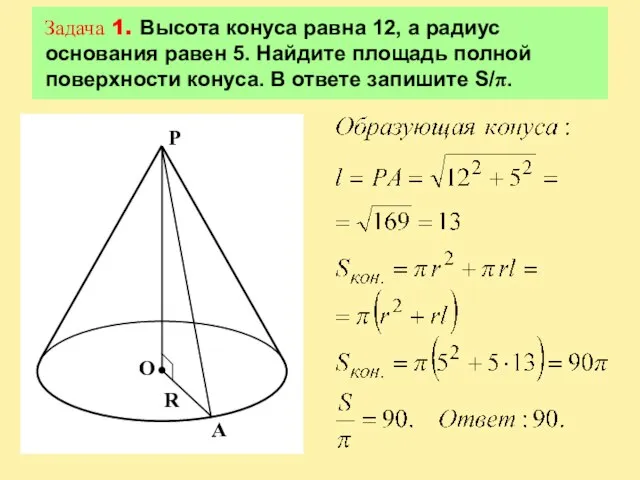
площадь полной поверхности конуса. В ответе запишите S/π.
Слайд 8Сечения конуса различными плоскостями
Секущая плоскость проходит через ось конуса.
Осевое сечение –
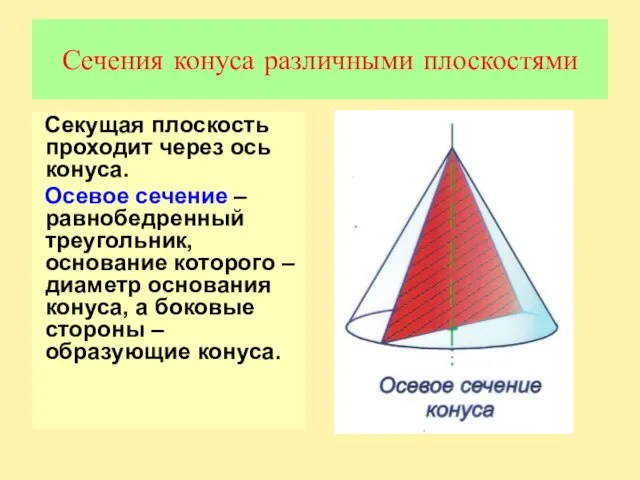
равнобедренный треугольник, основание которого – диаметр основания конуса, а боковые стороны – образующие конуса.
Слайд 9Сечения конуса различными плоскостями
Если секущая плоскость перпендикулярна к оси конуса, то сечение
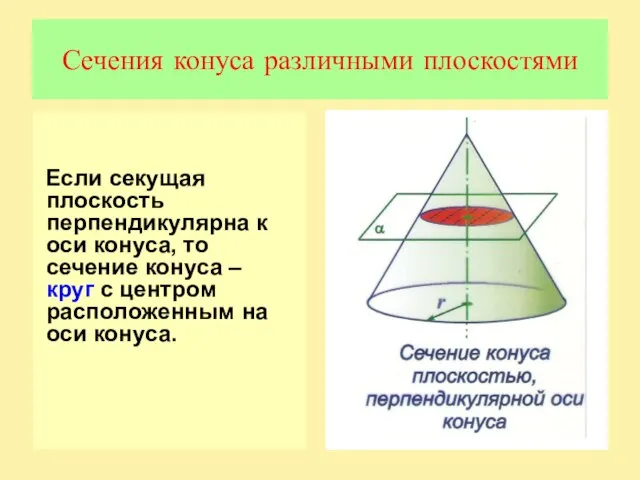
конуса – круг с центром расположенным на оси конуса.
Слайд 10Вписанная пирамида
Пирамида называется вписанной в конус, если ее основание есть многоугольник, вписанный
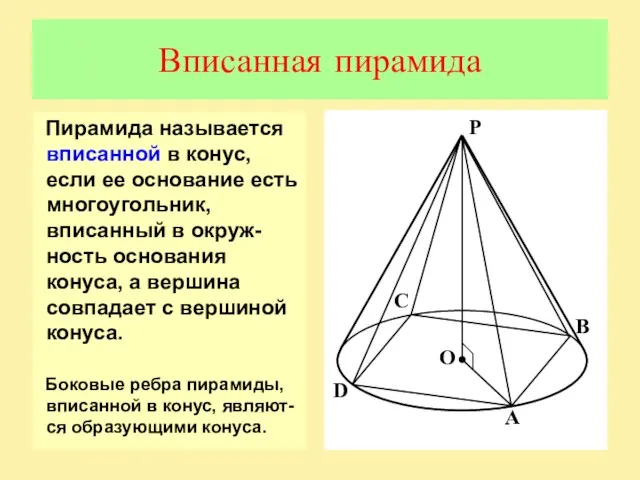
в окруж-ность основания конуса, а вершина совпадает с вершиной конуса.
Боковые ребра пирамиды, вписанной в конус, являют-ся образующими конуса.
Слайд 11Описанная пирамида
Пирамида называется описанной около кону-са, если ее основание есть многоугольник, описанный
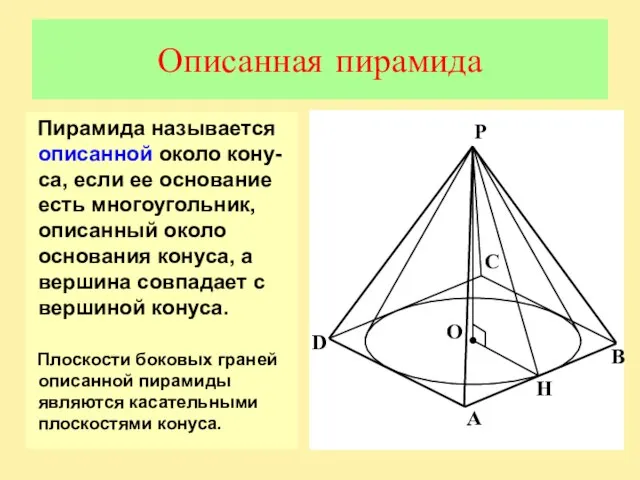
около основания конуса, а вершина совпадает с вершиной конуса.
Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса.
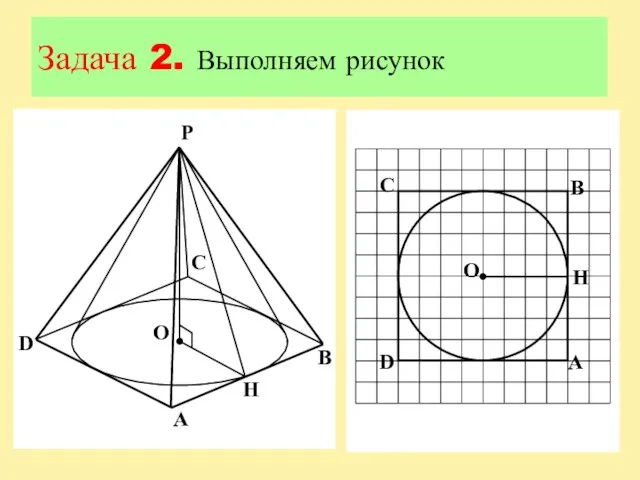
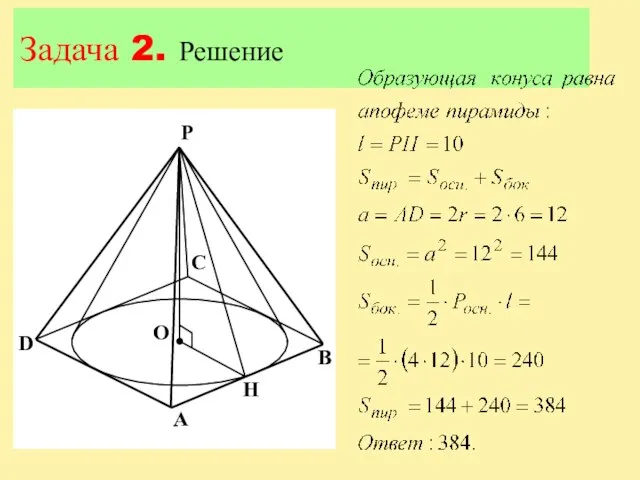
Слайд 12Задача 2
Вокруг конуса описана правильная четырехугольная пирамида. Найдите полную поверхность пирамиды, если

радиус основания конуса равен 6, а образующая конуса равна 10.
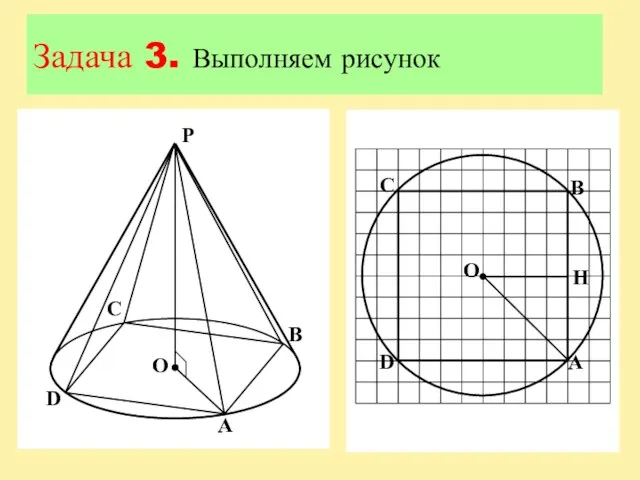
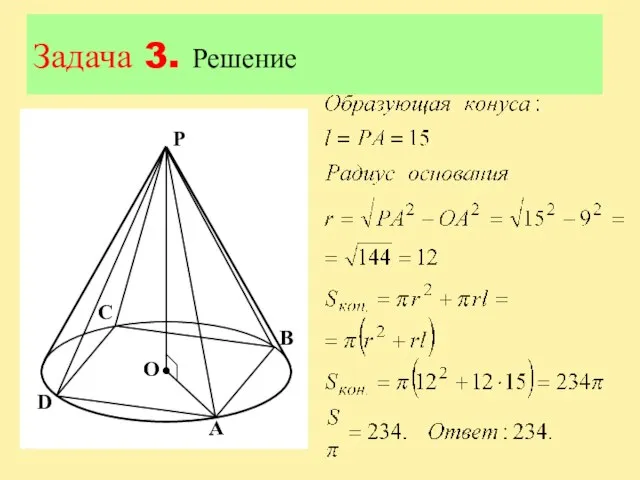
Слайд 15Задача 3
В конус вписана правильная четырехугольная пирамида. Найдите полную поверхность конуса, если

боковое ребро пирамиды равно 15, а ее высота равна 9. В ответе запишите S/π.
Слайд 18Аннотация:
Данная презентация разработана для уроков геометрии в 11 классе по теме «Конус».

В работе рассмотрены понятия конуса и его элементов, «поверхность конуса», формула поверхности конуса, сечения конуса плоскостями. Рассмотрены так же понятия пирамиды, описанной около конуса, пирамиды, вписанной в конус. В презентации рассмотрены задачи из «Открытого банка заданий по математике», для закрепления рассмотренных понятий.













 Реформа языка Карамзина
Реформа языка Карамзина Варианты расчета бонуса за два месяца
Варианты расчета бонуса за два месяца Эксплуатация автомобильного транспорта
Эксплуатация автомобильного транспорта Государство в политической системе
Государство в политической системе ИСТОРИЯ СПИЧЕК
ИСТОРИЯ СПИЧЕК Презентация на тему Растения-индикаторы
Презентация на тему Растения-индикаторы Мышление как психический процесс. Виды и формы мышления. 4 формата мышления
Мышление как психический процесс. Виды и формы мышления. 4 формата мышления Субъекты правовых отношений. Правовое положение лиц
Субъекты правовых отношений. Правовое положение лиц скульптура «Под одними звездами» ("Unter den gleichen Sternen")
скульптура «Под одними звездами» ("Unter den gleichen Sternen") Виды гимнастики
Виды гимнастики Hilton Hotels & Resorts
Hilton Hotels & Resorts Шар. Елка. Снеговик
Шар. Елка. Снеговик Обзор православной литературы Доброе слово для малых ребят
Обзор православной литературы Доброе слово для малых ребят Водные маршруты
Водные маршруты Презентация на тему Василий Тёркин
Презентация на тему Василий Тёркин  Технология приготовления пиццы
Технология приготовления пиццы Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В.
Мир в свечах Выполнила: Плаксунова Людмила МОУ СОШ №4 Руководитель: Чуприна Т.В. "Поле - чудес" по произведениям К.И. Чуковского
"Поле - чудес" по произведениям К.И. Чуковского PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha
PURE_THERAPY_Bezuprechnaya_idealno_ochischennaya_kozha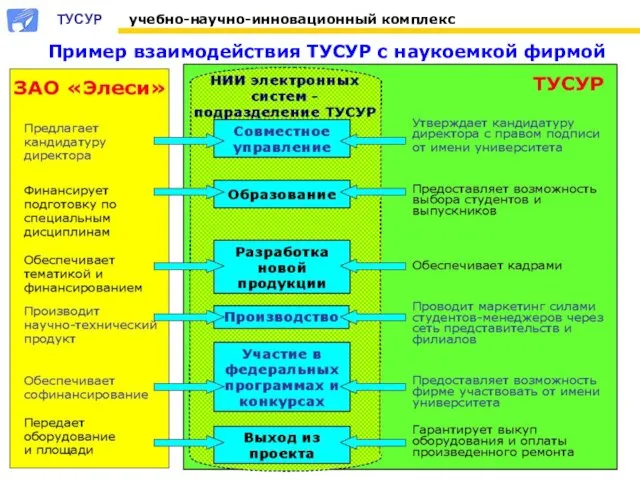 Пример взаимодействия ТУСУР с наукоемкой фирмой
Пример взаимодействия ТУСУР с наукоемкой фирмой Введение в менеджмент
Введение в менеджмент Австралия
Австралия Who should be the first ?
Who should be the first ? Велосипедный туризм
Велосипедный туризм Музей восстания машин
Музей восстания машин Презентация "Художники пореформенной России" - скачать презентации по МХК
Презентация "Художники пореформенной России" - скачать презентации по МХК Хочу отдыхать
Хочу отдыхать Сенситивные периоды человека (методика Марии Монтессори)
Сенситивные периоды человека (методика Марии Монтессори)