Содержание
- 2. Цели урока: Научиться раскладывать произвольный вектор по координатным векторам. Отработать навыки действий над векторами с заданными
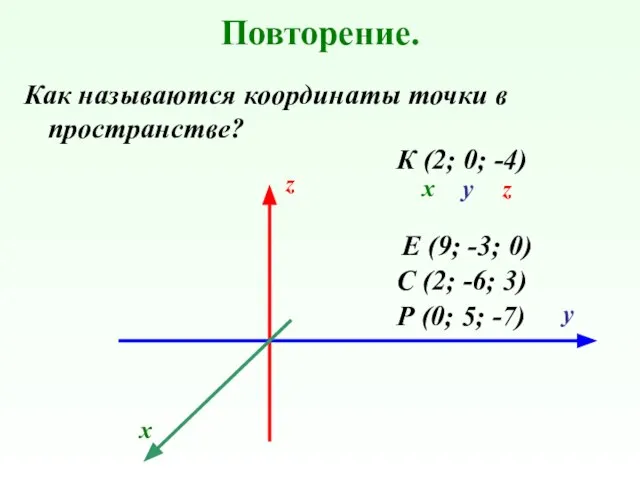
- 3. Повторение. Как называются координаты точки в пространстве? Р (0; 5; -7) К (2; 0; -4) С
- 4. Повторение. Даны точки: А (2; -1; 0) В (0; 0; -7) С (2; 0; 0) D
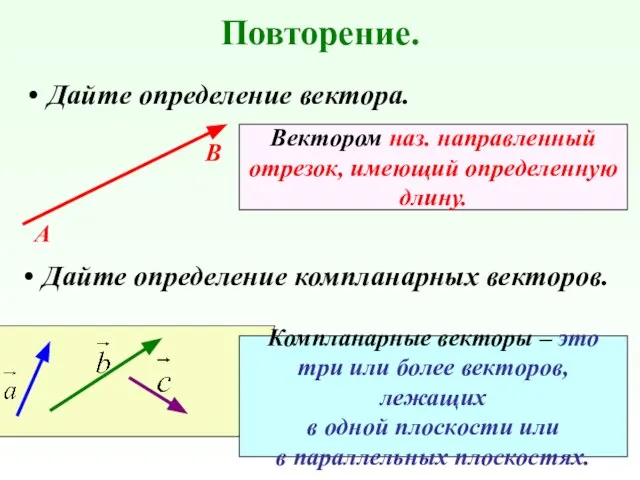
- 5. Повторение. Дайте определение вектора. А В Вектором наз. направленный отрезок, имеющий определенную длину. Дайте определение компланарных
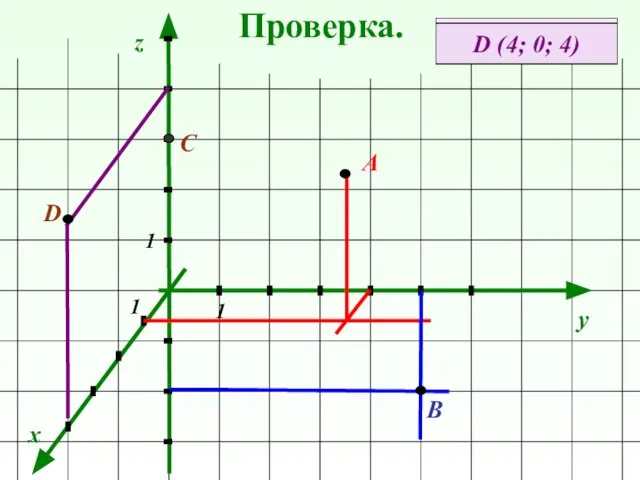
- 6. Выполнение задания с последующей проверкой. Начертить прямоугольную трехмерную систему координат и отметить в ней точки: А
- 7. Проверка. x y z А (1; 4; 3) А В (0; 5; -3) 1 1 1
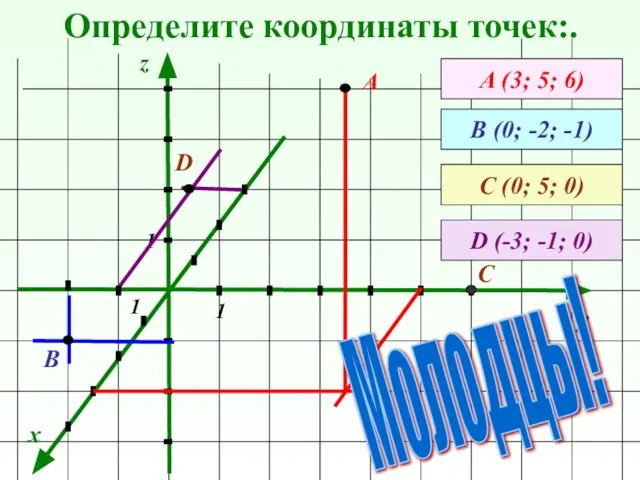
- 8. Определите координаты точек:. x y z А (3; 5; 6) А В (0; -2; -1) 1
- 9. Думаем… Отвечаем… Даны точки А (2; 4; 5), В (3; а; b), C (0; 4; d)
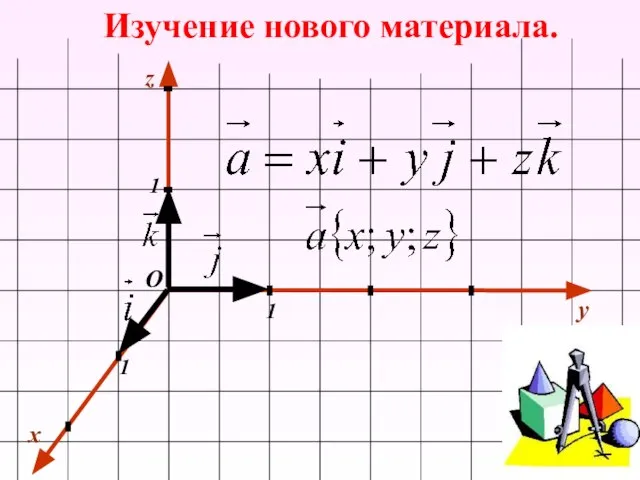
- 10. Изучение нового материала. x y 1 1 1 О z
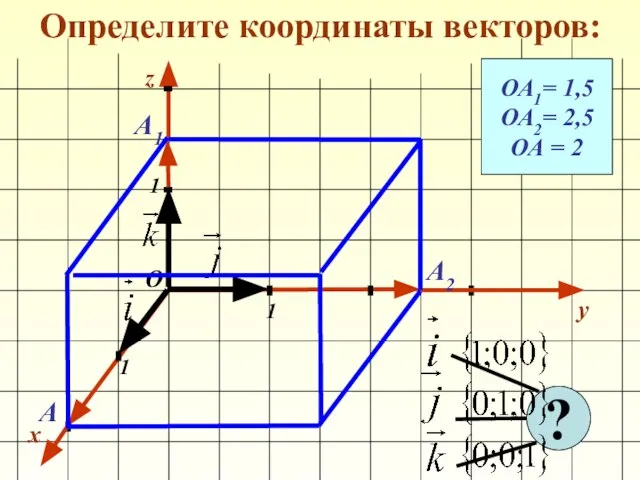
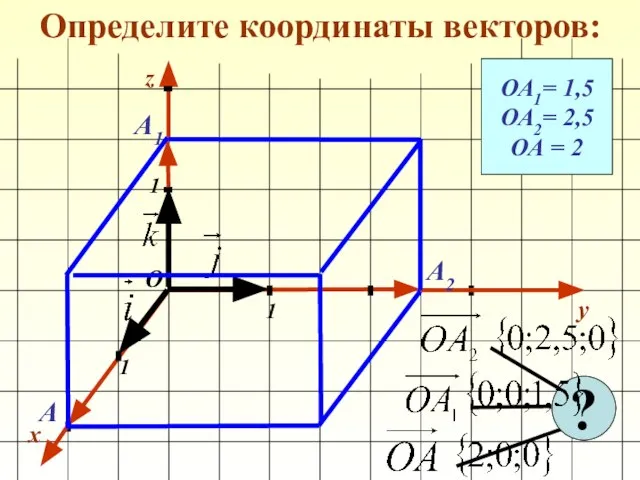
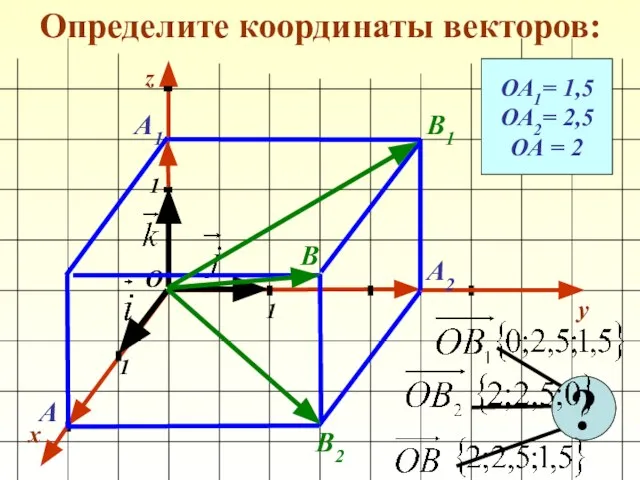
- 11. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
- 12. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
- 13. Определите координаты векторов: x y 1 1 1 О z ОА1= 1,5 ОА2= 2,5 ОА =
- 14. Разложите все векторы по координатным векторам. Проверяем:
- 15. Правила действий над векторами с заданными координатами. 1. Равные векторы имеют равные координаты. Пусть , тогда
- 16. Правила действий над векторами с заданными координатами. 2. Каждая координата суммы двух (и более) векторов равна
- 17. Правила действий над векторами с заданными координатами. 3. Каждая координата произведения вектора на число равна произведению
- 18. Домашнее задание: №№ 403, 404, 407 Доказательства двух правил действий над векторами. Повторить определение средней линии
- 19. Выполнить задание устно: Даны векторы: Найти вектор равный:
- 20. Письменно: №№ 403; 404; № 407 – по вариантам. I вариант – а, в, д. II
- 22. Скачать презентацию










 Unusual traditions of birthday celebrations
Unusual traditions of birthday celebrations Автомобили контейнерые и контейнеры
Автомобили контейнерые и контейнеры Коррекционно-образовательное значение литературы в обучении школьников с ТНР
Коррекционно-образовательное значение литературы в обучении школьников с ТНР Муниципальное образовательное учреждение для детей дошкольного и младшего школьного возраста «Начальная школа – детский сад с.
Муниципальное образовательное учреждение для детей дошкольного и младшего школьного возраста «Начальная школа – детский сад с. Зевс. Бог неба, грома и молний, ведающий всем миром
Зевс. Бог неба, грома и молний, ведающий всем миром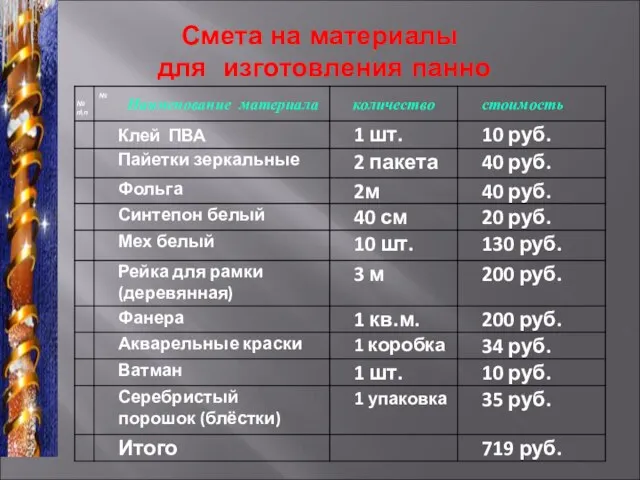 Смета на материалы для изготовления панно
Смета на материалы для изготовления панно Творческая биография А.Н. Бенуа
Творческая биография А.Н. Бенуа Ландшафтная архитектура
Ландшафтная архитектура Влияние Великой Отечественной войны на развитие химической науки. Вклад ученых-химиков в Победу.
Влияние Великой Отечественной войны на развитие химической науки. Вклад ученых-химиков в Победу. www.e-society.mk Ширењето на хакерскиот дух (интернет, слободен софтвер и нови медиуми) Новица Наков Слободен софтвер Македонија
www.e-society.mk Ширењето на хакерскиот дух (интернет, слободен софтвер и нови медиуми) Новица Наков Слободен софтвер Македонија Презентация на тему Риск. Виды рисков, методы нейтрализации рисков
Презентация на тему Риск. Виды рисков, методы нейтрализации рисков  Оптика 11 класс
Оптика 11 класс Популяризация театра
Популяризация театра Молекулярные машины
Молекулярные машины Confusing words: rubbish, garbage, trash, litter, waste, junk, debris
Confusing words: rubbish, garbage, trash, litter, waste, junk, debris Certificate
Certificate Домик из фруктов
Домик из фруктов Перестановка слагаемых (1 класс)
Перестановка слагаемых (1 класс) Eastern cousine
Eastern cousine ВКР: Выбор варианта доставки крупногабаритной строительной техники из республики Корея в Российскую Федерацию
ВКР: Выбор варианта доставки крупногабаритной строительной техники из республики Корея в Российскую Федерацию Методика применения электронного учебного пособияпо базовому курсу информатики Руководитель проекта: Огарков А.Ю., учитель инфо
Методика применения электронного учебного пособияпо базовому курсу информатики Руководитель проекта: Огарков А.Ю., учитель инфо АКЦИЯ «ТЕРРИТОРИЯ ЗДОРОВОГО ПИТАНИЯ» в г.Новосибирске 2009г.
АКЦИЯ «ТЕРРИТОРИЯ ЗДОРОВОГО ПИТАНИЯ» в г.Новосибирске 2009г. Избирательная система в РФ
Избирательная система в РФ Тестоделители и тестоокруглители
Тестоделители и тестоокруглители Crm. Клиентские исследования. Управление поведением. Лояльность
Crm. Клиентские исследования. Управление поведением. Лояльность Тоннелдегі бұрғылауаттыру жұмыстарын маркшейдерлік жұмыспен қамтамасыз ету
Тоннелдегі бұрғылауаттыру жұмыстарын маркшейдерлік жұмыспен қамтамасыз ету Семейство Бобовые и Пасленовые
Семейство Бобовые и Пасленовые Spraw, abyśmy wrócili do Twojej jedności
Spraw, abyśmy wrócili do Twojej jedności