Содержание
- 2. Показатели , характеризующие центральную тенденцию ряда Математическое ожидание Мода Медиана Выход Математическим ожиданием выборки называется сумма
- 3. Показатели , характеризующие центральную тенденцию ряда Математическое ожидание Мода Медиана Выход В этом случае: М(Х)=2* 1/20+
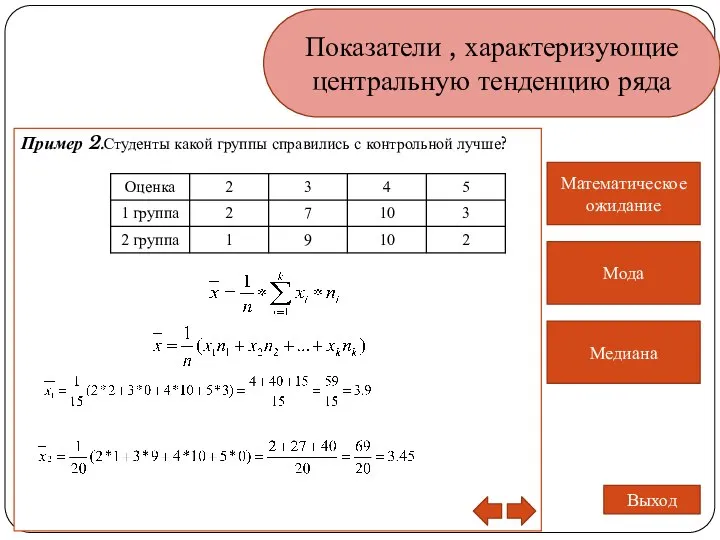
- 4. Показатели , характеризующие центральную тенденцию ряда Математическое ожидание Мода Медиана Выход Пример 2.Студенты какой группы справились
- 5. Показатели , характеризующие центральную тенденцию ряда Математическое ожидание Мода Медиана Выход Среднее арифметическое 2х групп 1
- 6. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход Мода - это наиболее часто
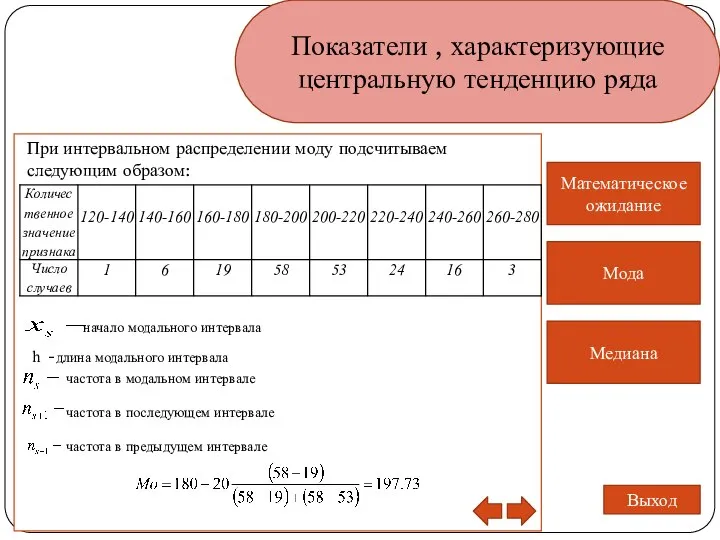
- 7. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход При интервальном распределении моду подсчитываем
- 8. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход При интервальном распределении моду подсчитываем
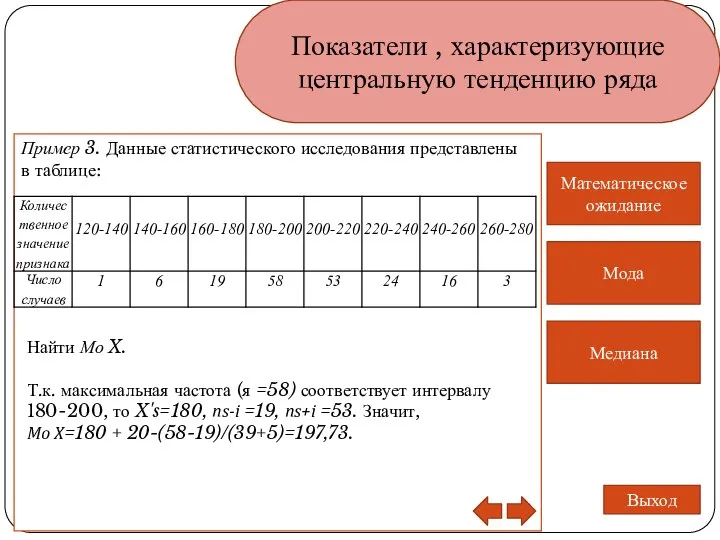
- 9. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход Пример 3. Данные статистического исследования
- 10. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход Медианой МеХ называется значение признака,
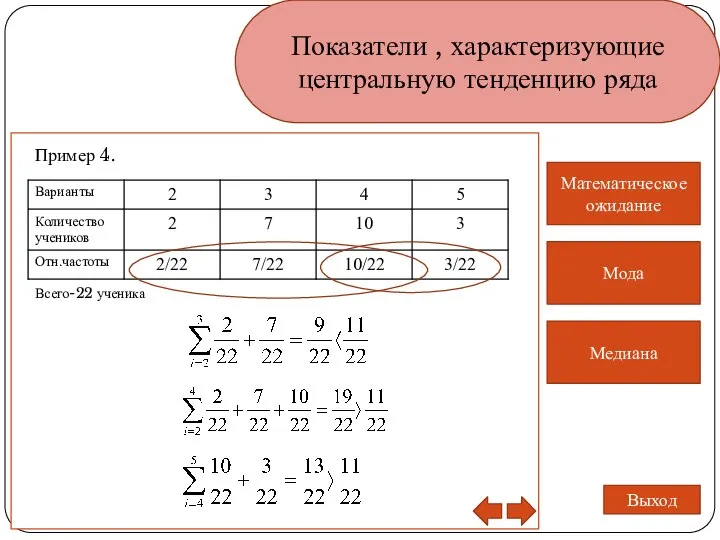
- 11. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход Пример 4. Всего-22 ученика
- 12. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход Для определения медианы по интервальному
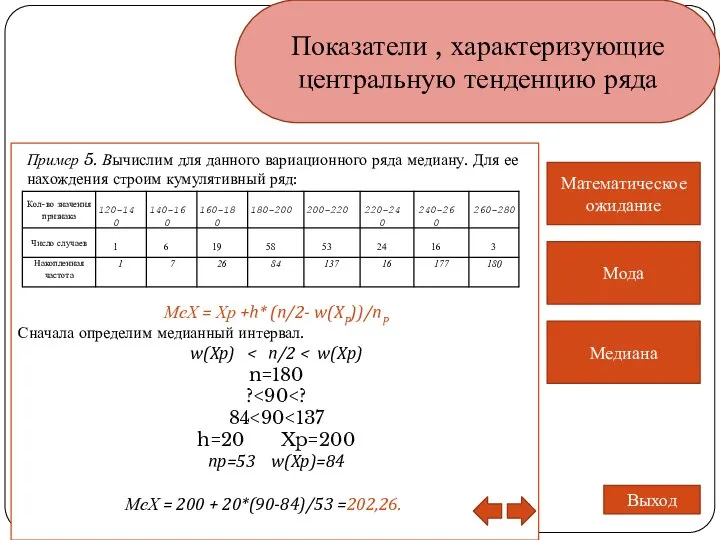
- 13. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход Пример 5. Вычислим для данного
- 14. Показатели , характеризующие центральную тенденцию ряда Медиана Математическое ожидание Мода Выход Найдем для каждой группы точное
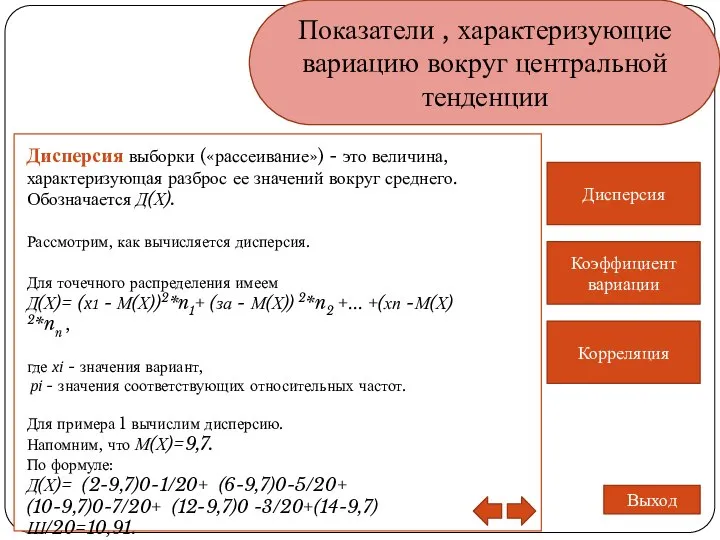
- 15. Показатели , характеризующие вариацию вокруг центральной тенденции Дисперсия Коэффициент вариации Корреляция Выход Дисперсия выборки («рассеивание») -
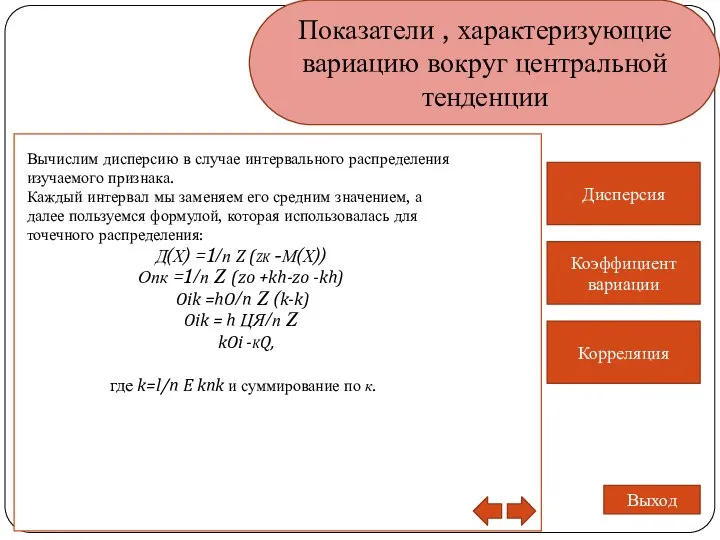
- 16. Показатели , характеризующие вариацию вокруг центральной тенденции Дисперсия Коэффициент вариации Корреляция Выход Вычислим дисперсию в случае
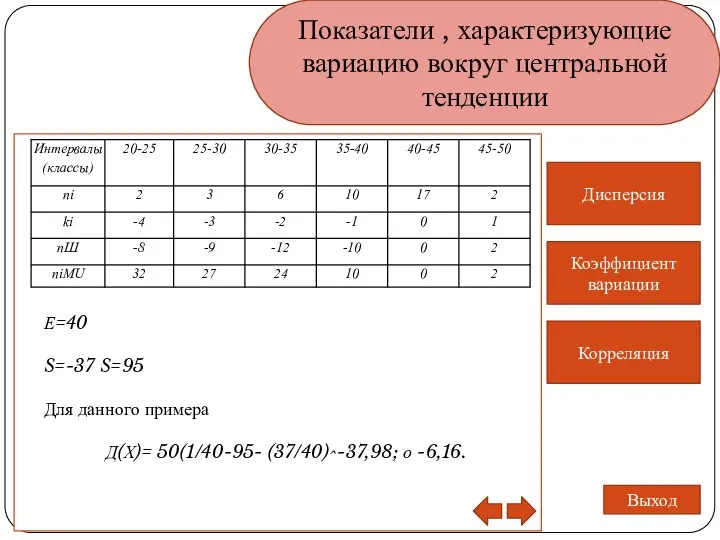
- 17. Показатели , характеризующие вариацию вокруг центральной тенденции Дисперсия Коэффициент вариации Корреляция Выход Е=40 S=-37 S=95 Для
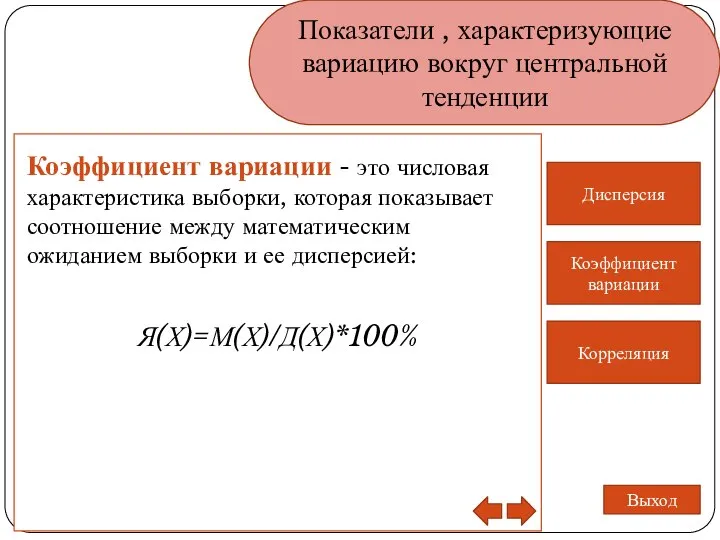
- 18. Показатели , характеризующие вариацию вокруг центральной тенденции Дисперсия Коэффициент вариации Корреляция Выход Коэффициент вариации - это
- 19. Показатели , характеризующие вариацию вокруг центральной тенденции Дисперсия Коэффициент вариации Корреляция Выход Связи (зависимости) между двумя
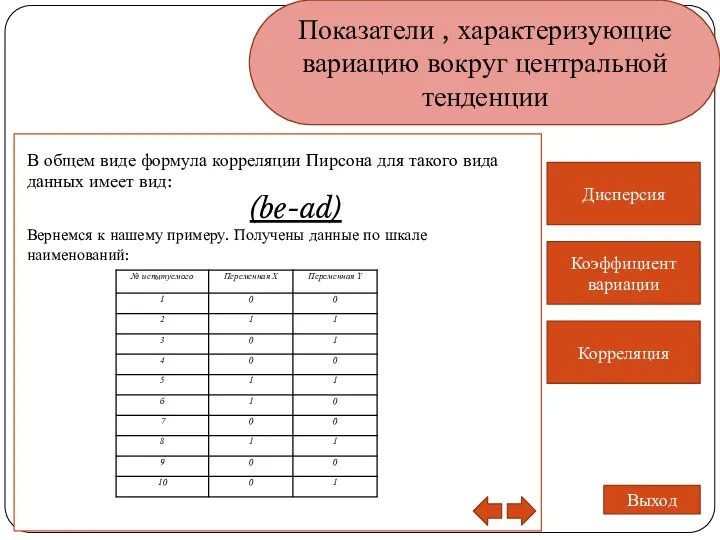
- 20. Показатели , характеризующие вариацию вокруг центральной тенденции Дисперсия Коэффициент вариации Корреляция Выход В общем виде формула
- 22. Скачать презентацию









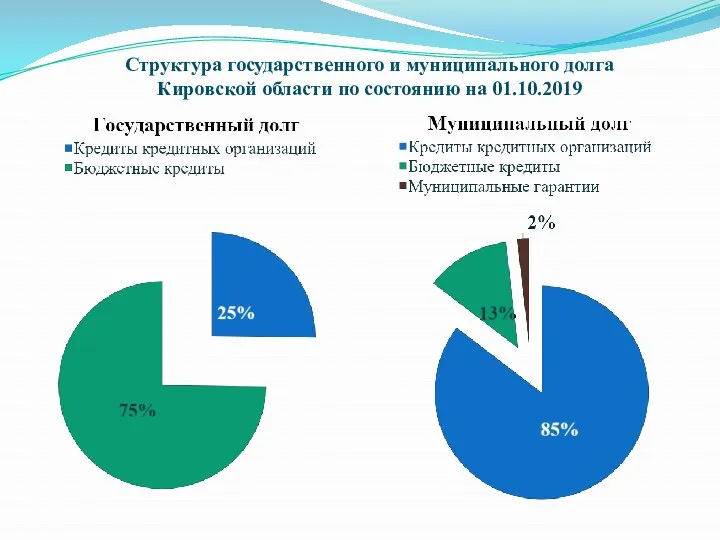 Структура государственного и муниципального долга Кировской области по состоянию на 01.10.2019
Структура государственного и муниципального долга Кировской области по состоянию на 01.10.2019 Передовые технологии, основанные на традициях
Передовые технологии, основанные на традициях Шедевры мировой живописи
Шедевры мировой живописи Гнетовидные
Гнетовидные Храмы, построенные после 1990 года
Храмы, построенные после 1990 года Презентация на тему Галицко-Волынское княжество
Презентация на тему Галицко-Волынское княжество  Национальная предпринимательская инициатива по улучшению инвестиционного климата в Российской Федерации Дорожная карта инициа
Национальная предпринимательская инициатива по улучшению инвестиционного климата в Российской Федерации Дорожная карта инициа Масленица
Масленица Презентация на тему Профилактика суицида
Презентация на тему Профилактика суицида Когда изобрели велосипед
Когда изобрели велосипед История открытия клеточного строения
История открытия клеточного строения Семья. Семейные традиции. 4 класс
Семья. Семейные традиции. 4 класс Презентация на тему Работа с историческими датами
Презентация на тему Работа с историческими датами  Преломление света
Преломление света Юридические лица
Юридические лица Специфика организации тренировочного процесса у баскетболистов
Специфика организации тренировочного процесса у баскетболистов Презентация на тему Органы дыхания окружающий мир 3 класс
Презентация на тему Органы дыхания окружающий мир 3 класс Инновационное развитие экономики России: Институциональная среда
Инновационное развитие экономики России: Институциональная среда Живописная композиция в интерьере с небольшим количеством персонажей
Живописная композиция в интерьере с небольшим количеством персонажей О формировании нормативной базы проектирования объектов переработки ПНГ, хранения и транспорта СУГ (ШФЛУ)
О формировании нормативной базы проектирования объектов переработки ПНГ, хранения и транспорта СУГ (ШФЛУ) Построение развивающей образовательной среды как перспективная цель образовательного учреждения
Построение развивающей образовательной среды как перспективная цель образовательного учреждения Себестоимость продукции
Себестоимость продукции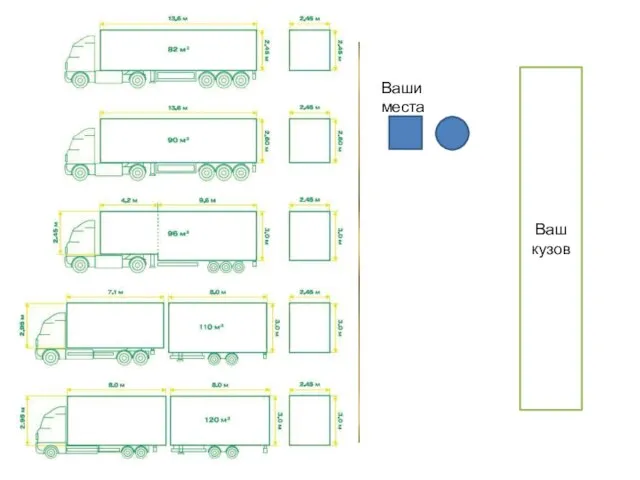 Ваши места. Ваш кузов
Ваши места. Ваш кузов Презентация на тему Проблемы культуры речи подростков
Презентация на тему Проблемы культуры речи подростков рекомендации
рекомендации Квалификационная работа«Духовно-нравственное воспитание школьников на уроках истории, обществознания и во внеклассной работе,
Квалификационная работа«Духовно-нравственное воспитание школьников на уроках истории, обществознания и во внеклассной работе,  Преемственность основны образовательных программ ДОУ и НОО
Преемственность основны образовательных программ ДОУ и НОО Кукушкина Светлана Ивановна, учитель французского языка и истории
Кукушкина Светлана Ивановна, учитель французского языка и истории