Космология

2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей

Закон Хаббла (продолжение)
Интерпретируя сдвиг длин волн как результат эффекта Допплера, скорость галактик пропорциональна этому сдвигу
На самом деле это не эффект Допплера!!!
Итак, скорость удаления галактики пропорцио-нальна расстоянию до неё
Значит ли это, что вблизи нашей Галактики произошел гигантский взрыв?

Закон Хаббла
Итак, в случае линейной зависимости удаление всех тел не означает существования центра расширения
Все тела удаляются от всех!
Но когда-то тела были ближе... Может даже все галактики, вся Вселенная расширяется из одной точки...

2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей

Красное смещение
Сдвиг длины волны определяют как
z = ( – 0) / 0, где
0 – длина волны, измеренная в лаборатории
 – наблюдаемая длина волны
Обычно ее называют красным смещением, так как
Если z > 0, то  > 0 – линия сдвигается в сто-рону больших длин волн («красная» сторона)
В космологии чаще всего z > 0

Красное смещение
Причины для изменения длины волны
Эффект Допплера (взаимное движение источника и наблюдателя)
Гравитационное смещение (различные гравитационные потенциалы источника и наблюдателя)
Расширение пространства (фотон «расши-ряется», пока движется в пространстве)
Старение фотонов (фотон «краснеет» из-за свойств пространства)

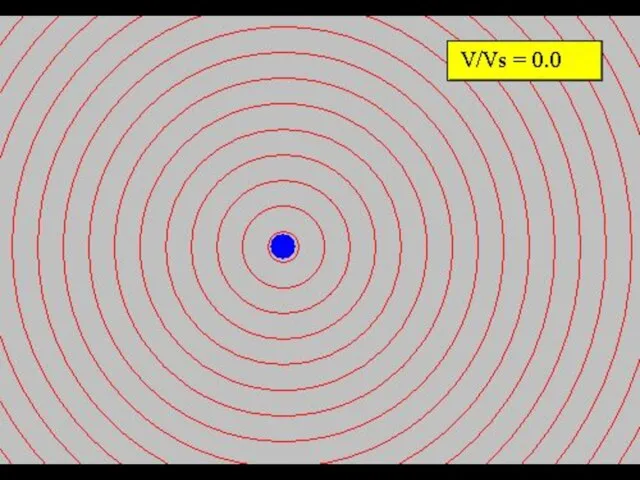
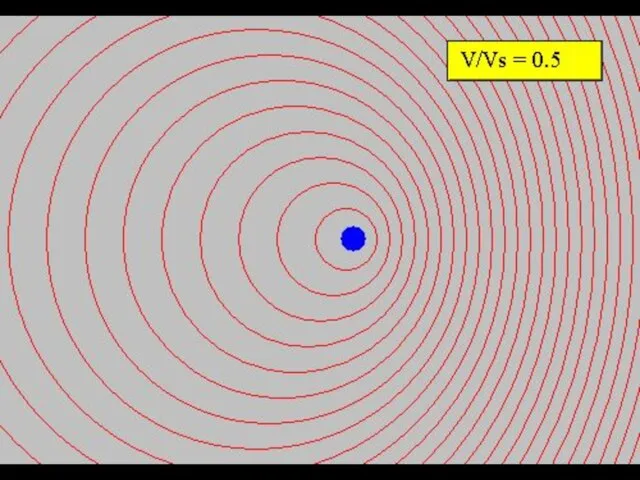
Эффект Допплера
Длина волны изменяется из-за того, что наблюдатель движется и изменяется проме-жуток времени между пучностями волны света
Из-за изменения частоты меняется и регистрируемая длина волны
При взаимном удалении источника и наблюдателя возникает красное смещение, при сближении – фиолетовое смещение

Эффект Допплера
Точная формула:
v – модуль скорости относительного движения
 - угол между направлением движения источника и линией наблюдения
c – скорость света в вакууме
Примерная формула при v << c

Расширение пространства
Длина волны изменяется, так как в течение свободного движения фотона пространство успело расшириться и «растянуть» фотон
При расширении пространства возникает красное смещение, при сжатии – фиолетовое смещение

Расширение пространства
Интегральная формула:
a – масштабный фактор (показывает, во сколько раз пространство расширилось по сравнению с определенным моментом)
a2 соответсвует времени регистрации фотона, а a1 – времени излучения
Дифференциальная формула:
a = da/dt

Красное смещение
Так как красное смещение галактики складывается из действия обоих эффектов, то
Причина закона Хаббла – расширение пространства, а разброс вокруг прямой даёт эффект Допплера, который вызывают случайные движения отдельных галактик относительно центра масс скопления галактик

Суть постоянной Хаббла
Размерность постоянной Хаббла – км/с/Мпк или просто 1/с
Она показывает, насколько в относитель-ных единицах расширяется пространство в единицу времени
Значит, величина, обратная постоянной Хаббла, приблизительно разна возрасту Вселенной

Метагалактика
Отсюда следует, что у Вселенной есть предел наблюдаемой области
Наблюдаемую часть Вселенной называют Метагалактикой
Расстояние до границы Метагалактики примерно RМ = c / H0 = 1.3·1026 м

2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей

Космологические модели
Космологической моделью называют математическую модель, описывающую усредненное распределение материи в пространстве и его эволюцию
Модели делят на классы по теории, в рамках которой она построена:
Ньютоновская космология – всемирный закон притяжения
Релятивистская космология – ОТО

Космологические модели
Основные предположения, на которых основываются все космологические модели:
Вселенная однородна и изотропна
Законы физики одинаковы во всей Вселенной
Применимость этих предположений следует из многих данных различных наблюдений

Ньютоновская космология
Рассмотрим «типичный» шар, равномерно заполненный материей.
Пусть радиальные скорости частиц под-чиняются закону Хаббла (что неизбежно при наших предположениях):
Пусть H>0 и не зависит от пространст-венных координат (только от времени)

Ньютоновская космология
Пусть в момент времени t0 координата частицы есть . Тогда эта координата меняется по закону (R(t) – масштабный фактор).
Так как , то

Ньютоновская космология
Для определения зависимости R(t) и H(t) от времени, используем законы сохранения массы и полной механической энергии.
Масса шара не меняется
или, записывая по другому,

Ньютоновская космология
Закон сохранения механической энергии для элемента на краю шара:
Кинетическая энергия
Потенциальная энергия
Полная энергия постоянна:

Ньютоновская космология
Запишем полную механическую энергию (постоянную) в виде . Тогда
(*)

Ньютоновская космология
Это уравнение вместе с начальными условиями полностью определяют R(t), т.е. все динамические свойства космологической модели.
В уравнение (*) не входит размер шара материи, поэтому его можно применять для шара любого размера, как и для всей Вселенной, равномерно заполненной веществом.

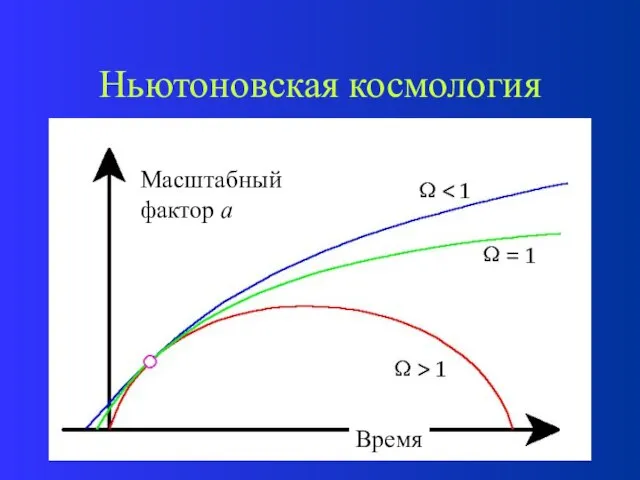
Ньютоновская космология
Качественно можно оценить R(t) даже без интегрирования уравнения (*):

Ньютоновская космология
Если k<0, то полная механическая энергия положительна (кинетическая больше потенциальной) и данный элемент объёма будет вечно отдаляться от начала координат.
Если k>0, то полная энергия отрицательна. Через какое-то время расширение затормозится и сменится сжатием (H<0)
k=0 – пограничный случай:

Ньютоновская космология
Знак постоянной k и характер движения материи зависит от знака разности , где
называют критической плотностью. Введём также обозначение

Ньютоновская космология
Если , то расширение шара остановится и сменится сжатием.
Если , то расширение будет продолжаться вечно.
Значение критической плотности (как и сама плотность) меняется со временем, но знак разности плотностей не меняется.

Ньютоновская космология
Решим уравнение эволюции (*) в случае, когда k = 0.

Ньютоновская космология

Ньютоновская космология
Масштабный
фактор а
Время

Ньютоновская космология
Классическая космология Ньютона применима лишь малым интервалам пространства и времени (локально)
Качественно верно описывает эволюцию вселенной и ее зависимость от средней плотности
Неприменима для описания всей вселенной, так как скорость взаимо-действия считается бесконечной

2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей

Релятивистская космология
Согласно экспериментальным данным, скорость света постоянна во всех системах отсчета.
Это противоречит теории Ньютона, но верно в специальной теории относительности (СТО)
Но в СТО не включено гравитационное взаимодействие. Теория, описывающая и его, учитывая конечность скорости взаимодействия, есть ОТО.

История
В 1916 году А. Эйнштейн создает общую теорию относительности (ОТО)
Она рассматривает объекты, которые движутся с большими скоростями в сильных гравитационных полях
Он (и другие) ищут решения ОТО для описания эволюции Вселенной
Вселенную представляют однородной и изотропной (космологический принцип)

История
В 1917 году А. Эйнштейн создает модель стационарной вселенной, дополняя урав-нения гравитационного поля «-членом»
В 1917 году В. де Ситтер находит реше-ние для динамической пустой вселенной
Закон Хаббла (1929 г.) соответствует ожиданиям ОТО и соответствует случаю расширения Вселенной

История
Albert Einstein (1879 – 1955)
W. de Sitter
(1872 – 1934)

История
В 1922 году А.А. Фридман и, независимо от него, в 1927 году Г.Е. Леметр развили далее модель нестационарной вселенной, учитывая массу, гравитацию и кривизну пространства
Согласно этой теории вселенная расширя-ется из начальной пространственно-вре-менной сингулярности до современного состояния и дальше

История
Александр Фридман
(1888 – 1925)
Abbe Lemaitre

2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей

Основные понятия
Основные понятия ньютоновской теории гравитации
Однородное и изотропное пространство, в котором происходит движение
Однородное время как параметр движения
Движущаяся масса
Гравитационное взаимодействие, моментально действующее по закону

Основные понятия
Основные понятия СТО
Пространство-время Минковского
Инерциальная система отсчета (ИСО)
Скорость света c, с которой распространяются взаимодействия
Что отсутствует в этой теории
Гравитационное поле

Основные понятия ОТО
Локально-инерциальная система отсчета (ЛИСО), которая вводится из-за невозможности построения единой глобальной ИСО в пространстве с гравитационным полем.
В СТО ускорение тела может быть скомпенсировано ускорением система отсчета. В ОТО это невозможно.

Основные понятия ОТО
Пространство-время Римана – кривое 4-х мерное пространство (т.е. элемент интервала ds нельзя глобально преобразовать в форму Минковского)
Геометрические свойства (кривизну) определяет движение и распределение массы. Но и само движение определя-ется кривизной пространства.

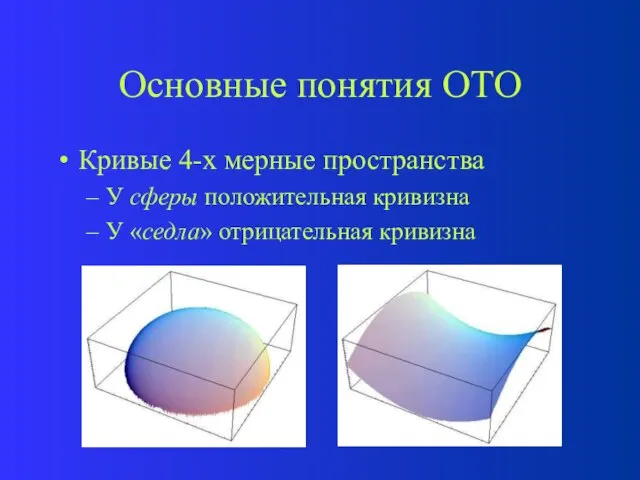
Основные понятия ОТО
Кривые 4-х мерные пространства
У сферы положительная кривизна
У «седла» отрицательная кривизна

Основные понятия ОТО
Согласно ОТО, гравитационное поле проявляется в кривизне пространства. Чем больше отличие от плоского пространства, тем сильнее поле.
Уравнения гравитационного поля ОТО – система десяти нелинейных дифференциальных уравнений второго порядка

Уравнения Эйнштейна
Кривизну с распределением массы связывают уравнения Эйнштейна
Rik и R=gikRik характеризуют кривизну
gik – метрический тензор
Tik характеризует распределение и движение материи
 – постоянная Эйнштейна

Тензор энергии-импульса
Рассмотрим вид тензора энергии-импульса Tik в наиболее частых случаях
Компонента T00 равна плотности энергии вещества  = c2
Компоненты Tii (i = 1, 2, 3) равны давлению вещества p
Недиагональные члены в ЛИСО – нули

Тензор энергии-импульса
Тензор энергии-импульса для пыли:
Пыль определена как среда с низкой темпе-ратурой (т.е. тепловые скорости движения много меньше скорости света с)
Отсюда давление пыли равно нулю и единственная ненулевая компонента тензора Tik есть

Тензор энергии-импульса
Тензор энергии-импульса для ультра-релятивистских частиц:
Их 4-импульс равен
Тогда , где  - плотность энергии
И

Тензор энергии-импульса
Открытый вид тензора энергии-импульса для ультра-релятивистского вещества (в его системе отсчета):
Для излучения (фотонов) Tik такой же!

Уравнение состояния
Давление с плотностью вещества связано уравнением вещества, общий вид которого p = c2
Из вида тензора Tik следует, что для пыли  = 0, а для ультра-релятивистского вещества и излучения  = 1/3
Наша Вселенная

2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей

Фридмановские модели
Основные приближения
Пространство однородно и изотропно
Описание системы происходит в ЛИСО
Тогда уравнения Эйнштейна сводятся к
Наша Вселенная

Фридмановские модели
Основные приближения
Пространство однородно и изотропно
Материя есть «пыль»
Тогда уравнения Эйнштейна сводятся к

Фридмановские модели
Эти уравнения не независимы, и второе из них эквивалентно уравнению (*), если на место T00 подставить его значение c2

Фридмановские модели
Хотя уравнения математически иден-тичны, они описывают разную «физику»

Фридмановские модели
Но так как уравнения идентичны, то и решения тоже одинаковы!

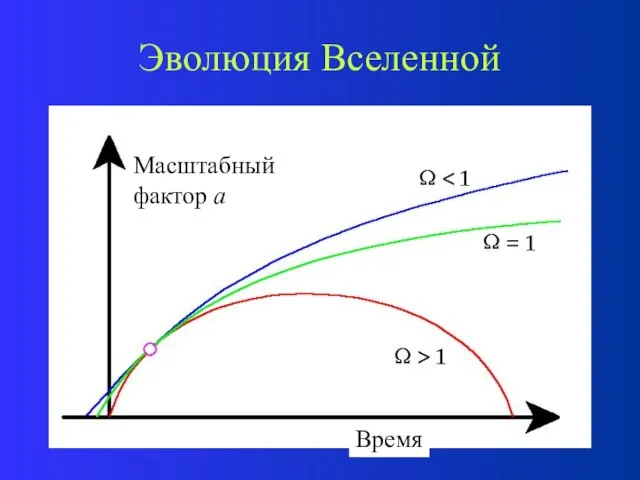
Эволюция Вселенной
Эволюция зависит от одного параметра – параметра плотности .
Если  < 1, то вселенная вечно расширя-ется. Пространство открыто.
Если  > 1, то вселенная после стадии расширения начинает сжиматься обратно. Пространство замкнуто.
Если  = 1, то пограничный случай – пространство плоское

Эволюция Вселенной
Масштабный
фактор а
Время

Эволюция Вселенной
Постоянная Хаббла – мера скорости изменения масштаба Вселенной а:
Со временем она меняется!
При наблюдении объекта рассчитанная постоянная Хаббла зависит от эволюции вселенной во все моменты между излучением и регистрацией фотона

2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей

Наша Вселенная
Мы рассмотрели общую схему эволюции вселенной, заполненной пылевидной материей
Возникает закономерный интерес – годится ли разработанная теория для описания нашей Вселенной
И если годится, то каковы реальные значения параметров модели?

Наша Вселенная
Преобразуем уравнение Фридмана (УФ), учитывая форму Tik (Tik). Итак,
Оно показывает, что эволюция зависит от уравнения состояния p = c2

Наша Вселенная
Во Вселенной одновременно есть типы материи с разными значениями 
Последние данные (WMAP, февраль 2003 года) убедительно показывают, что около 2/3 от общей энергии занимает т.н. тёмная энергия
Попробуем понять, что же это такое!
Если не хотят понять

 - член
Исторически первая модель вселенной Эйнштейна (1917 г.) была по построению статичной. Однако, как мы видели, уравнения Эйнштейна не допускают такое решение
Чтобы решить это противоречие, Эйнштейн добавил в уравнения дополни-тельный скалярный член (т.н. -член)

 - член
Уравнения Эйнштейна:
Уравнения, дополненные -членом

 - член
Найдём эффективное уравнение состоя-ния -члена. Для этого представим себе, что материи вообще нет. Тогда
Эффективный тензор энергии-импульса в ЛИСО есть

 - член
Сравнивая с общим видом тензора энергии импульса в ЛИСО, т.е.
видим, что для -члена  = – 1.
Значит, если плотность энергии -члена доминирует, то Вселенная расширяется ускоренно!

 - член
Действительно, из уравнения Фридмана:
Если  = – 1 (т.е. всю плотность энергии составляет -член), то d2a/dt2 положите-лен и расширение происходит ускоренно.
Причина – сильное отрицательное «давление»

Наша Вселенная
Итак, обычное вещество с   0 способствует сжатию Вселенной, а -член – ее расширению.
Так как в нашей Вселенной доминирует -член, то она будет расширятся вечно и ускоренно.
Пока на ясна физическая причина существования ненулевого -члена. К примеру, это могла бы быть энергия вакуумных нулевых флуктуаций...

2 лекция
Космологические модели
Закон Хаббла
Красное смещение
Ньютоновская космология
Релятивистская космология
Основы ОТО
Фридмановские модели
Наша Вселенная
Обобщение космологических моделей

Модель эволюции Вселенной
Обобщим закономерности, выведенные на этой лекции
Выведем зависимости характеристик вещества от времени для
Пыли
Ультра-релятивистского вещества и излучения
Космологической постоянной
Фотоны - всегда
ультра-релятивистские частицы

Состояния вещества
Пыль:
Плотность энергии 
Давление p = 0,  = 0
Ультра-релятивистское вещество и излучение:
Плотность энергии  = c2
Давление p = 1/3 ,  = 1/3
Космологическая постоянная :
Плотность энергии  = 
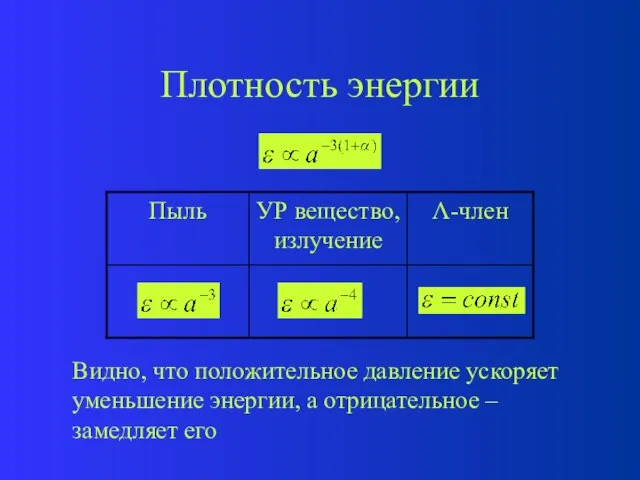
Давление p = -,  = -1

Плотность энергии
Уравнение, описывающее зависимость плотности энергии  от масштабного фактора a:

Плотность энергии
Видно, что положительное давление ускоряет уменьшение энергии, а отрицательное – замедляет его

Масштабный фактор
Уравнение Фридмана описывает зависи-мость масштабного фактора от времени:

Масштабный фактор
Если   -1, то
Если  = -1, то
Зависимость истинна, если данный тип
вещества доминирует во Вселенной

Постоянная Хаббла
Если a(t) – степенная функция, то посто-янная Хаббла обратно пропорциональна времени
Если a(t) – экспонента, то постоянная Хаббла не зависит от времени

Температура
Зависимость температуры излучения от а есть , так как плотность энергии излучения есть
Зависимость температуры пыли от времени не так проста, так как на нее влияют эффекты выделения внутренней энергии (притяжение, ядерные и химические реакции и др.)

Параметры вещества

Выводы
Узнали главные экспериментальные факты внегалактической астрономии
Ознакомились с некоторыми моделями эволюции Вселенной на основе теории Ньютона и ОТО
На следующей лекции проследим эволюцию Вселенной с точки зрения теории Большого Взрыва