Содержание
- 2. RSA: Берем p,q- два больших простых числа(512 бит) n=pЧq, ϕ(n)=(p-1)Ч(q-1) e d-? : eЧd=1 (mod ϕ(n))
- 3. Encryption and Digital Signature Шифрование: MОZn(секретное сообщение) C=M^e(mod n) то, что мы посылаем получателю. D=С^d(mod n)
- 4. Полезный теоретический факт Пусть (N,e)-публичный ключ, d- закрытый ключ. Тогда зная (N,e,d) можно разложить N на
- 5. Полезный теоретический факт Пусть (N,e)-публичный ключ, d- закрытый ключ. Тогда зная (N,e,d) можно разложить N на
- 6. Теоретический факт Открытый вопрос: Пусть даны N,e:gcd(e,ϕ(n))=1 и F:Zn->Zn, F(x)=x^(1/e)(mod n) – вычисляется за единичное время.
- 7. Методы разложения N на простые сомножители Trial Division Pollard’s p-1 Method Pollard’s rho Method Elliptic Curve
- 8. Trial Division Пытаемся разделить n на все простые числа от 1 до Цn.
- 9. Trial Division Пытаемся разделить n на все простые числа от 1 до Цn. Плохой метод (работает
- 10. Trial Division Пытаемся разделить n на все простые числа от 1 до Цn. Плохой метод (работает
- 11. Pollard’s p-1 Method n=pq , у p-1 все простые делители k- произведение достаточно больших степеней всех
- 12. Pollard’s rho(ρ) Method Если у нас есть n исходов и 1.2*(n^1.2) испытаний то вероятность того, что
- 13. Pollard’s rho(ρ) Method Замечание Если считать для всех пар i и j gcd(xj-xi,n), то мы сделаем
- 14. Pollard’s rho(ρ) Method Замечание Если считать для всех пар i и j gcd(xj-xi,n), то мы сделаем
- 15. Pollard’s rho(ρ) Method Замечание Если считать для всех пар i и j gcd(xj-xi,n), то мы сделаем
- 17. Скачать презентацию














 Научно-Инновационное предприятие СКГМИ (ГТУ) "Стройкомплект-Инновации"
Научно-Инновационное предприятие СКГМИ (ГТУ) "Стройкомплект-Инновации" Скандинавский стиль
Скандинавский стиль WEB- браузеры
WEB- браузеры Биологическая безопасность и современные подходы к обеззараживанию воздуха в помещениях ЛПУ
Биологическая безопасность и современные подходы к обеззараживанию воздуха в помещениях ЛПУ Эволюционно-генетические аспекты иммунологии репродукции
Эволюционно-генетические аспекты иммунологии репродукции Подготовка к ЕГЭ Задания В1-В3 Вариант 3
Подготовка к ЕГЭ Задания В1-В3 Вариант 3 Строение тела человека
Строение тела человека Парейдолии в еде
Парейдолии в еде 1 Об итогах социально- экономического развития Сивинского муниципального района в сфере РЧП ФЦБ «РАЗВИТИЕ ЧЕЛОВЕЧЕСКОГО ПОТЕНЦИА
1 Об итогах социально- экономического развития Сивинского муниципального района в сфере РЧП ФЦБ «РАЗВИТИЕ ЧЕЛОВЕЧЕСКОГО ПОТЕНЦИА Презентация на тему Чехов "Злоумышленник" 7 класс
Презентация на тему Чехов "Злоумышленник" 7 класс Гибкие печатные платы
Гибкие печатные платы Экологические проблемы водоёмов
Экологические проблемы водоёмов Филиал ООО компания Тензор. Сфера торгов
Филиал ООО компания Тензор. Сфера торгов Сравнительная характеристика кредитных расчетов банков города Красноярска
Сравнительная характеристика кредитных расчетов банков города Красноярска ХИРУРГИЧЕСКАЯ АНАТОМИЯ КРУПНЫХ СУСТАВОВ КОНЕЧНОСТЕЙ
ХИРУРГИЧЕСКАЯ АНАТОМИЯ КРУПНЫХ СУСТАВОВ КОНЕЧНОСТЕЙ Питер Брейгель. Фламандские пословицы
Питер Брейгель. Фламандские пословицы Федеральный государственный образовательный стандарт дошкольного образования
Федеральный государственный образовательный стандарт дошкольного образования Презентация на тему Бангладеш
Презентация на тему Бангладеш  ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ
ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ Презентация на тему Здоров будешь - все добудешь
Презентация на тему Здоров будешь - все добудешь Фракталы вокруг нас
Фракталы вокруг нас Презентация на тему Ораторская речь,её особенности
Презентация на тему Ораторская речь,её особенности school
school Семейка самоцветов
Семейка самоцветов Йомаклы әлифба
Йомаклы әлифба Инвестиционные проекты, Казахстан
Инвестиционные проекты, Казахстан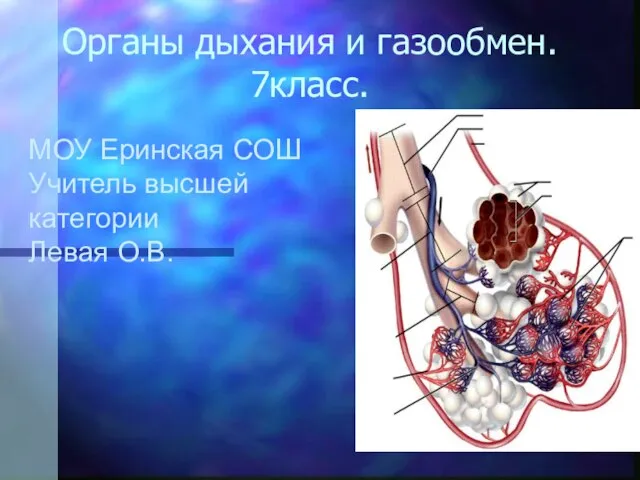 Органы дыхания и газообмен 7 класс
Органы дыхания и газообмен 7 класс Презентация на тему Новогодний сувенир в технике кистевой росписи
Презентация на тему Новогодний сувенир в технике кистевой росписи