Содержание
- 2. ГДЕ НАЧАЛО КУБА? Цель работы: Выяснить какие секреты хранит куб? Задачи: Во время исследования куба обнаружить
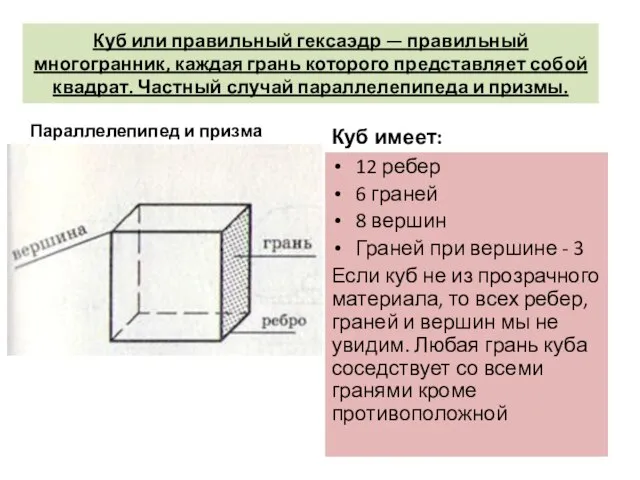
- 3. Куб или правильный гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда
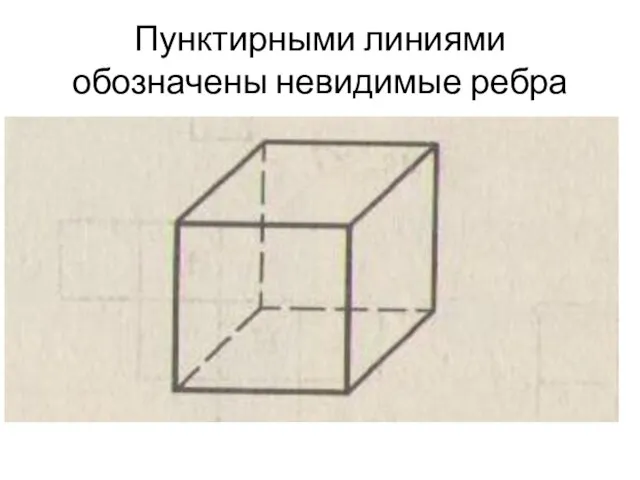
- 4. Пунктирными линиями обозначены невидимые ребра
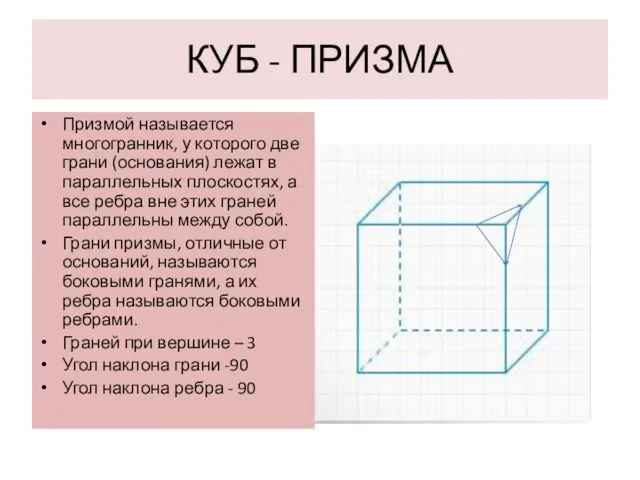
- 5. КУБ - ПРИЗМА Призмой называется многогранник, у которого две грани (основания) лежат в параллельных плоскостях, а
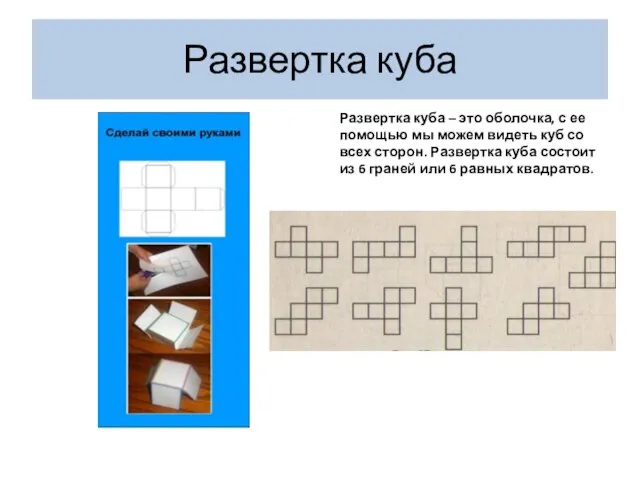
- 6. Развертка куба Развертка куба – это оболочка, с ее помощью мы можем видеть куб со всех
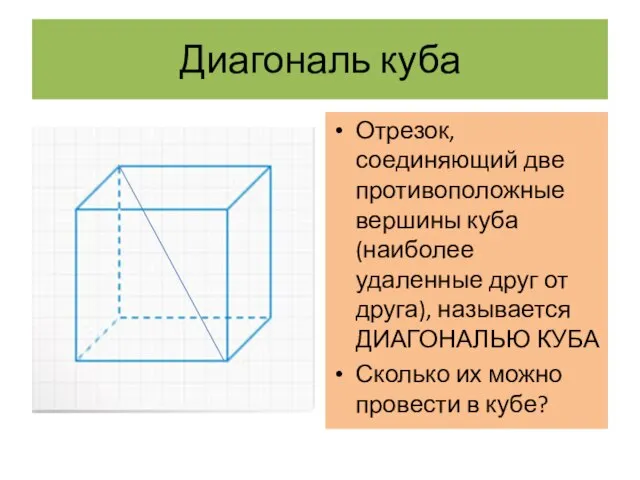
- 7. Диагональ куба Отрезок, соединяющий две противоположные вершины куба (наиболее удаленные друг от друга), называется ДИАГОНАЛЬЮ КУБА
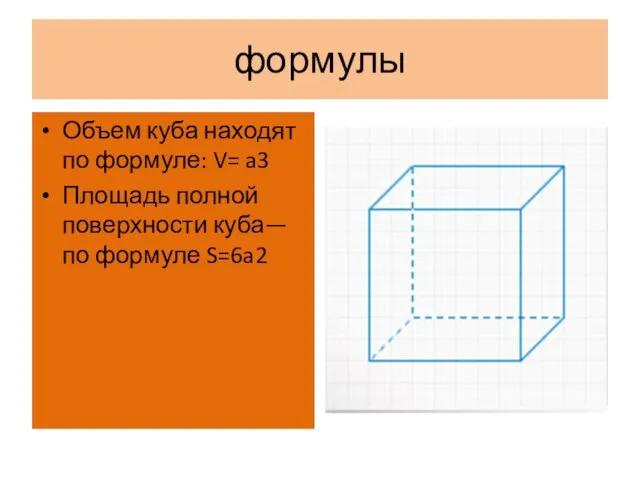
- 8. формулы Объем куба находят по формуле: V= a3 Площадь полной поверхности куба—по формуле S=6a2
- 9. ОБЪЕМЫ Куби́ческий киломе́тр (км³) — мера объёма, равная объёму куба с ребром 1 км. Подходит для
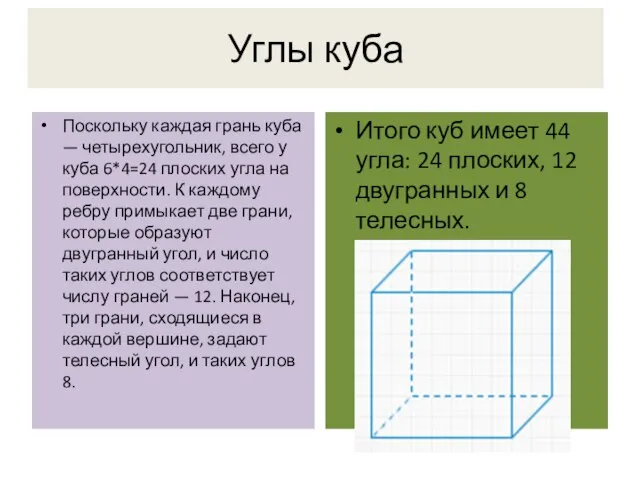
- 10. Углы куба Поскольку каждая грань куба — четырехугольник, всего у куба 6*4=24 плоских угла на поверхности.
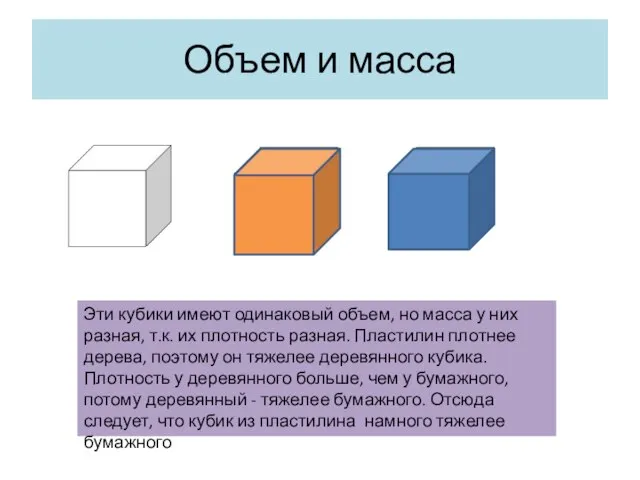
- 11. Объем и масса Эти кубики имеют одинаковый объем, но масса у них разная, т.к. их плотность
- 12. Где применяются кубы «Кубик Рубика» первоначально был известен как «Магический кубик», — механическая головоломка, изобретённая в
- 14. Скачать презентацию


 Презентация на тему Задачи на смеси и сплавы (9 класс)
Презентация на тему Задачи на смеси и сплавы (9 класс) Русская литература XX века: общая характеристика
Русская литература XX века: общая характеристика Денежные единицы мира
Денежные единицы мира Презентация на тему Золотой век Екатерины II
Презентация на тему Золотой век Екатерины II  Доходный подход к оценке
Доходный подход к оценке Музей Конфлуанс
Музей Конфлуанс Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ
Гендерные аспекты семейной политики Жанна Чернова НИУ-ВШЭ Презентация на тему Технология обработки древесины
Презентация на тему Технология обработки древесины Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье
Статистический анализ массовых наблюдений НЛО в восточном Оренбуржье Поняття ЕТ Excel
Поняття ЕТ Excel Налоги: сущность и виды. Классификация
Налоги: сущность и виды. Классификация Внутреняя энергия
Внутреняя энергия В стране правовых знаний
В стране правовых знаний Убранство русской избы
Убранство русской избы Политико-правовая теория Монтескье
Политико-правовая теория Монтескье 169601
169601 Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол
Отделение восстановительного леченияреабилитация* неврологические больные (22,1%)* кардиологические больные (20,2%)* * травматол Франсуа Виет и его теорема (8 класс)
Франсуа Виет и его теорема (8 класс) Может ли природа жить без человека?
Может ли природа жить без человека? Юридическая ответственность и её виды
Юридическая ответственность и её виды Осенняя одежда
Осенняя одежда Банк внешней торговли (Внешторгбанк)
Банк внешней торговли (Внешторгбанк)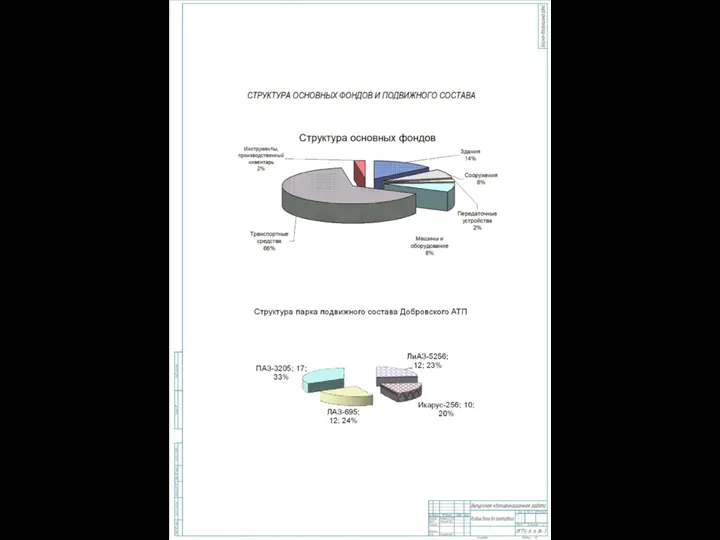 Структура основных фондов и подвижного состава
Структура основных фондов и подвижного состава Saint Isaac’s Square
Saint Isaac’s Square Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.
Агентство «Инсайт Маркетинг» решает задачи привлечения клиентов и повышения продаж при помощи инструментов интернет-маркетинга.  Педагогический совет
Педагогический совет Виды Смоленска
Виды Смоленска НАСС
НАСС