Kuv_2022_MS_13_Recons_авг (1)

Анализ данных, поступающих из систем измерения. Согласование данных

Материальный баланс
Лука Пачоли (годы жизни 1445г. – 1517г.) – математик из Италии, имя которого стало известно с момента обнаружения профессором математики Лючини в 1869 году в Миланском университете на забытых полках библиотеки известного на сегодняшний день каждому бухгалтеру Трактата о счетах и записях.
Ссылка на сайт: https://buhbook.net/buhgalterskij-uchet/istoriya-buhgalterskogo-ucheta/luka-pacholi-biografiya-osnovatelya-buhgalterskogo-ucheta-1445g-19-iyunya-1517g/
Примеры. Системы согласования баланса в промышленности (в нефтяной, пищевой, фармацевтической, распределение воды для снабжения городов, энергетика)
Под материальным балансом понимается концепция описания, основанная на законе сохранения масс, согласно которой извлечённая масса равна сумме изменения первоначальной и привнесённой в динамическую систему массы

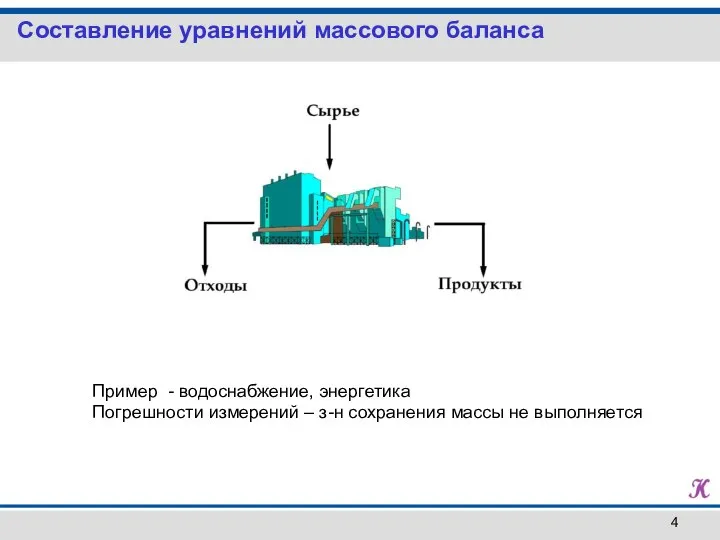
Составление уравнений массового баланса
Пример - водоснабжение, энергетика
Погрешности измерений – з-н сохранения массы не выполняется

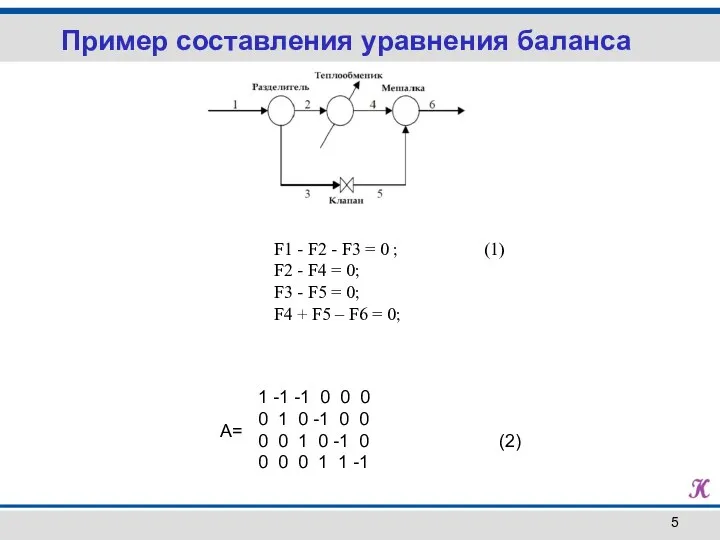
F1 - F2 - F3 = 0 ; (1)
F2 - F4 = 0;
F3 - F5 = 0;
F4 + F5 – F6 = 0;
1 -1 -1 0 0 0
0 1 0 -1 0 0
0 0 1 0 -1 0 (2)
0 0 0 1 1 -1
A=
Пример составления уравнения баланса

Согласование (сведение) уравнений массового баланса
В англоязычной литературе термин “data reconciliation” переводится как согласование данных и используется для математического обозначения термина сведение массового (материального) баланса. Основной целью согласования данных является вычисление так называемых истинных (согласованных) значений потоков и вычисление грубых ошибок измерений (“gross error detection”). Согласование производится на основе уравнений массового баланса и при этом должно соблюдаться правило минимума разницы (коррекции) между измеренными и согласованными величинами.
Пусть измеренное значение потока равно x0, а x будет истинное (реальное) значение потока, тогда:
x0 = x +ɛ, (3)
где ɛ – ошибка измерения.
Согласно правилу минимума разницы (коррекции) между измеренными и согласованными величинами можно потребовать, чтобы разница между измеренными и согласованными величинами в квадрате была минимальной (метод наименьших квадратов)

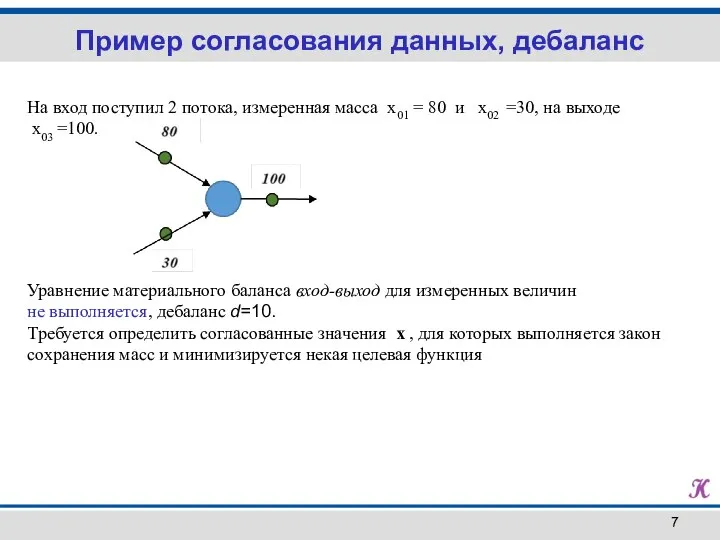
На вход поступил 2 потока, измеренная масса x01 = 80 и x02 =30, на выходе
x03 =100.
Уравнение материального баланса вход-выход для измеренных величин
не выполняется, дебаланс d=10.
Требуется определить согласованные значения x , для которых выполняется закон сохранения масс и минимизируется некая целевая функция
Пример согласования данных, дебаланс

Количество измерителей
Неизмеряемые потоки
Систематические и случайные погрешности
Диагностика неисправностей
Материальный и энергетический балансы
СОГЛАСОВАНИЕ ДАННЫХ ПРИБОРНОГО УЧЕТА

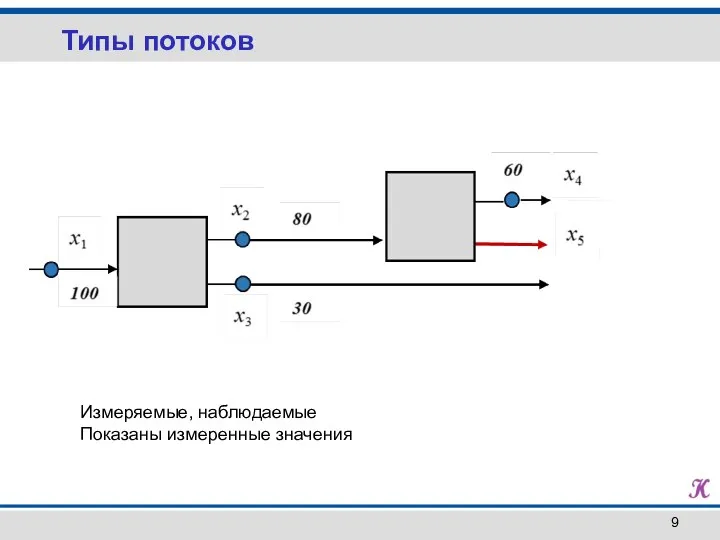
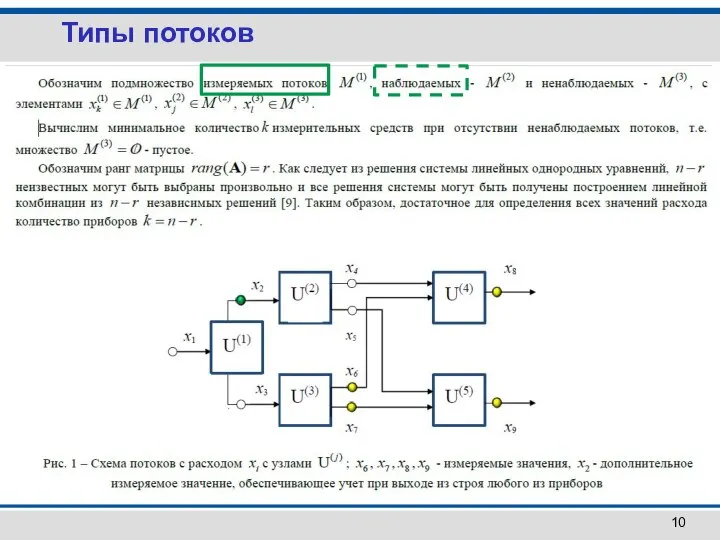
Типы потоков
Измеряемые, наблюдаемые
Показаны измеренные значения

Типы потоков

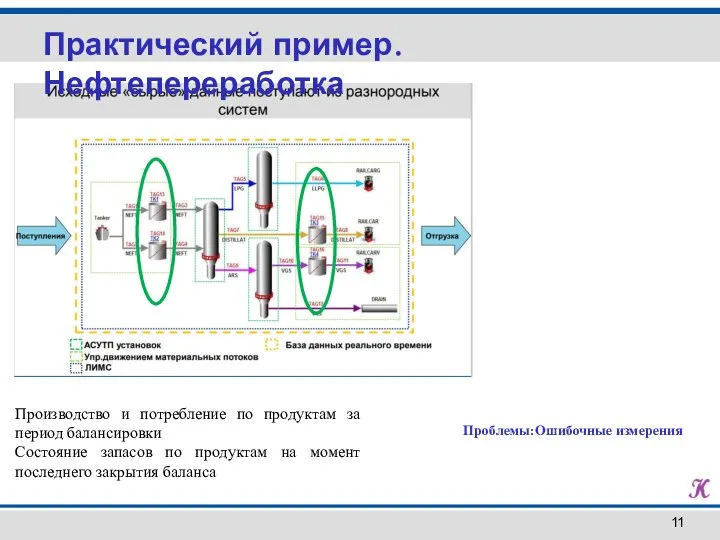
Практический пример. Нефтепереработка
Проблемы:Ошибочные измерения
Производство и потребление по продуктам за период балансировки
Состояние запасов по продуктам на момент последнего закрытия баланса

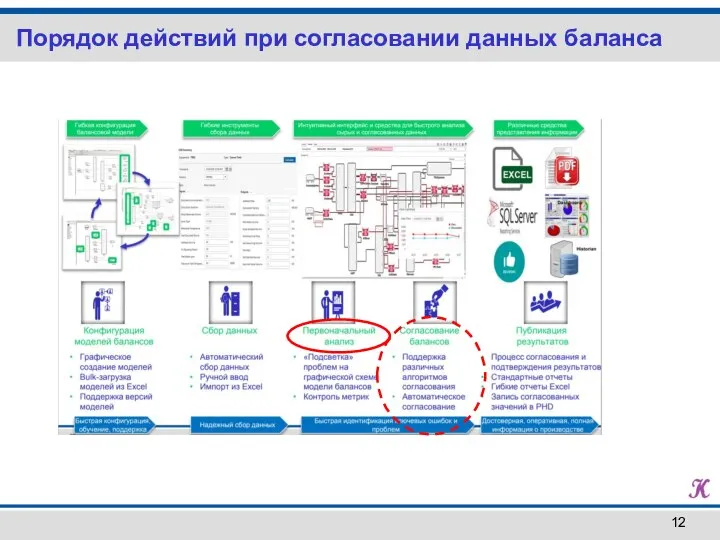
Порядок действий при согласовании данных баланса

Математическая статистика.
Обработка результатов измерений

Погрешности измерения
- погрешность измерения: разность между результатом измерения величины и действительным (опорным) значением величины;
- случайная погрешность измерения, случайная погрешность: составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью;
- систематическая погрешность измерения; систематическая погрешность: составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины, проведенных с одинаковой тщательностью;
- грубая погрешность измерения: погрешность измерения, существенно превышающая зависящие от объективных условий измерений значения систематической и случайной погрешностей.

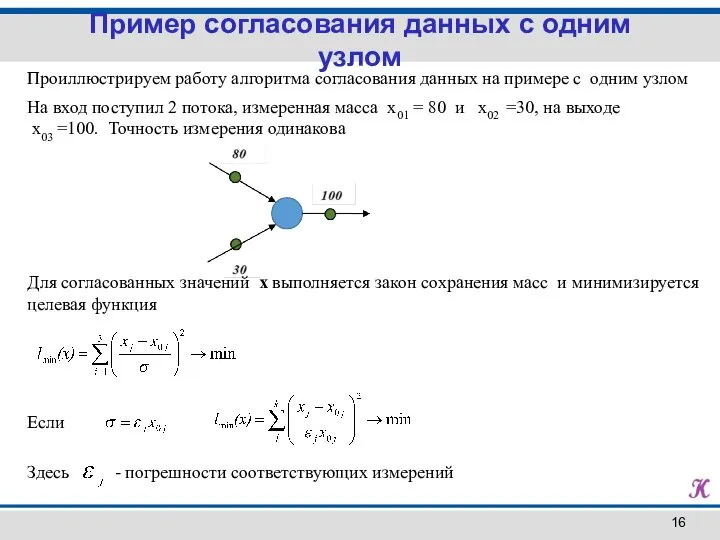
, (1)
где x – вектор согласованных переменных, описывающий массу материальных потоков предприятия, продукцию в резервуарах, расход топлива и потери, A- матрица балансовых уравнений размерности (элементы матрицы aij=1 для входящих потоков и aij=-1 - для выходящих, aij =0 - если поток не участвует в массовом балансе).
В качестве критерия оптимизации рассматривается функция ,
которая записывается в следующем виде
где B - матрица весовых коэффициентов, характеризующих погрешности соответствующих измерений, - дисперсия, q –количество измерений, - согласованные переменные для измеренных значений.
Физический смысл критерия (2) заключается в том, что решения системы уравнений (1), которые называются согласованными, должны как можно меньше отличаться от измеренных значений.
Математическая модель согласования данных
m – кол-во уравнений, n – кол-во переменных, q – кол-во измерений
(2)

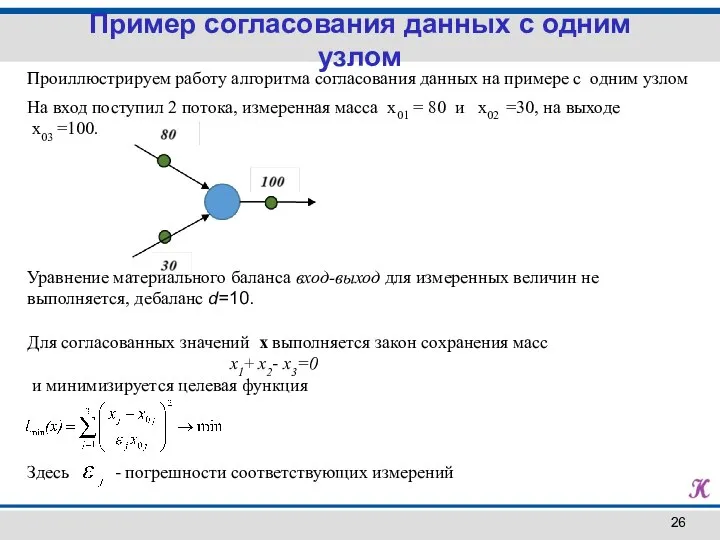
Проиллюстрируем работу алгоритма согласования данных на примере с одним узлом
На вход поступил 2 потока, измеренная масса x01 = 80 и x02 =30, на выходе
x03 =100. Точность измерения одинакова
Для согласованных значений x выполняется закон сохранения масс и минимизируется целевая функция
Здесь - погрешности соответствующих измерений
Пример согласования данных с одним узлом
Если

(Introduction to Gross Error Detection)
В некоторых случаях в измерениях может присутствовать так называемая грубая ошибка (gross error), которая возникает в случае смещения нуля, дрейфа значений вниз или вверх, а так же ухудшения точности.
Грубые ошибки отрицательно влияют на согласование данных и для точного согласования данных необходимо вначале, перед согласованием, устранить все грубые ошибки измерений, а потом уже согласовывать данные.
Определение грубых ошибок измерения – первый этап перед согласованием данных

Закон больших чисел. Правило корня из n
Ecли надо измерить некоторую величину, истинное значение которой равно а, проводят n независимых измерений этой величины. В качестве меры истинного значения случайной величины выбирается средняя арифметическая. Если при измерениях отсутствуют систематические погрешности (искажающие результат измерения в одну и ту же строну) естественно предположить, что математическое ожидание M(ξi)=a при любом i.
На основании теоремы Чебышева средняя арифметическая результатов n измерений сходится по вероятности к истинному значению а.
Если все измерения производятся с одинаковой точностью, характеризуемой дисперсией D(ξi)=σ2 , то дисперсия их средней
Таким образом, среднее квадратическое отклонение оказывается равным
Средний ожидаемый разброс средней из n измерений в корень квадратный из n раз меньше разброса каждого измерения (этот вывод известен под названием «правила корня из n»)

Замечание по точности измерения
Замечание. Если измерительный прибор имеет точность q (например, q- половина ширины деления шкалы прибора), то полученным способом нельзя получить точность измерения величины а , больше, чем q. Каждое измерение дает результат с неопределенностью q и среднее арифметическое будет обладать той же неопределённостью. (Н.Ш.Кремер)

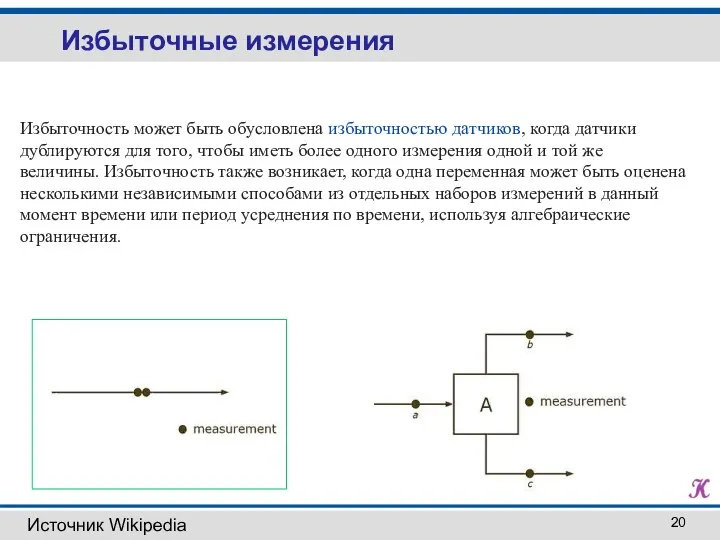
Избыточные измерения
Избыточность может быть обусловлена избыточностью датчиков, когда датчики дублируются для того, чтобы иметь более одного измерения одной и той же величины. Избыточность также возникает, когда одна переменная может быть оценена несколькими независимыми способами из отдельных наборов измерений в данный момент времени или период усреднения по времени, используя алгебраические ограничения.
Источник Wikipedia

Наблюдаемость
Избыточность может быть использована в качестве источника информации для перекрестной проверки и коррекции измерений и повышения их точности и точности: с одной стороны, они выверяются далее, проблема выверки данных, представленная выше, также включает в себя неизмеряемые переменные. Основываясь на информационной избыточности, оценки этих неизмеримых переменных могут быть рассчитаны вместе с их точностью. В промышленных процессах эти неизмеримые переменные, которые обеспечивает согласование данных, называются мягкими или виртуальными датчиками (soft sensors or virtual sensors), где аппаратные датчики не установлены.
Избыточность связана с понятием наблюдаемости. Переменная (или система) является наблюдаемой, если модели и измерения датчиков могут быть использованы для однозначного определения ее значения (состояния системы). Датчик является избыточным, если его удаление не приводит к потере наблюдаемости.

СОГЛАСОВАНИЕ ДАННЫХ
Data validation and reconciliation
Валидация и согласование данных промышленных процессов, или, более кратко, согласования данных (process data reconciliation PDR)- это технология, которая использует информацию о процессах и математические методы для автоматического обеспечения валидации и согласования данных путем коррекции измерений в промышленных процессах. Использование PDR позволяет извлекать точную и достоверную информацию о состоянии промышленных процессов из исходных данных измерений и получать единый согласованный набор данных, представляющих наиболее вероятную технологическую операцию.

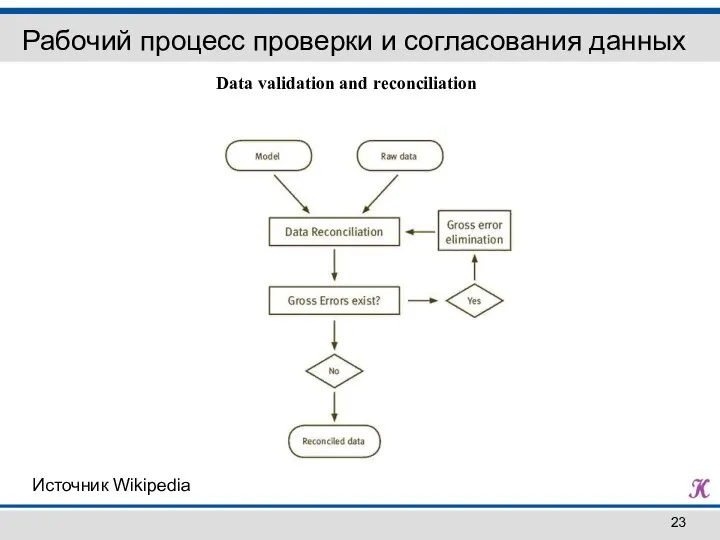
Рабочий процесс проверки и согласования данных
Источник Wikipedia
Data validation and reconciliation

Квадратичное программирование (quadratic programming, QP) — задача оптимизации (минимизации или максимизации) квадратичной функции нескольких переменных при линейных ограничениях на эти переменные. Квадратичное программирование является частным случаем нелинейного программирования.
Ограничения – равенства
Задача квадратичного программирования несколько проще, если Q является положительно определённой и все ограничения являются равенствами (нет неравенств), поскольку в этом случае можно свести задачу к решению системы линейных уравнений.
Методы решения

Алгоритм последовательного квадратичного программирования
Последовательное квадратичное программирование (Sequential quadratic programming (SQP)) — один из наиболее распространённых и эффективных оптимизационных алгоритмов общего назначения, основной идеей которого является последовательное решение задач квадратичного программирования, аппроксимирующих данную задачу оптимизации. Для оптимизационных задач без ограничений алгоритм SQP преобразуется в метод Ньютона поиска точки, в которой градиент целевой функции обращается в ноль. Для решения исходной задачи с ограничениями-равенствами метод SQP преобразуется в специальную реализацию ньютоновских методов решения системы Лагранжа.

Проиллюстрируем работу алгоритма согласования данных на примере с одним узлом
На вход поступил 2 потока, измеренная масса x01 = 80 и x02 =30, на выходе
x03 =100.
Уравнение материального баланса вход-выход для измеренных величин не выполняется, дебаланс d=10.
Для согласованных значений x выполняется закон сохранения масс
x1+ x2- x3=0
и минимизируется целевая функция
Здесь - погрешности соответствующих измерений
Пример согласования данных с одним узлом

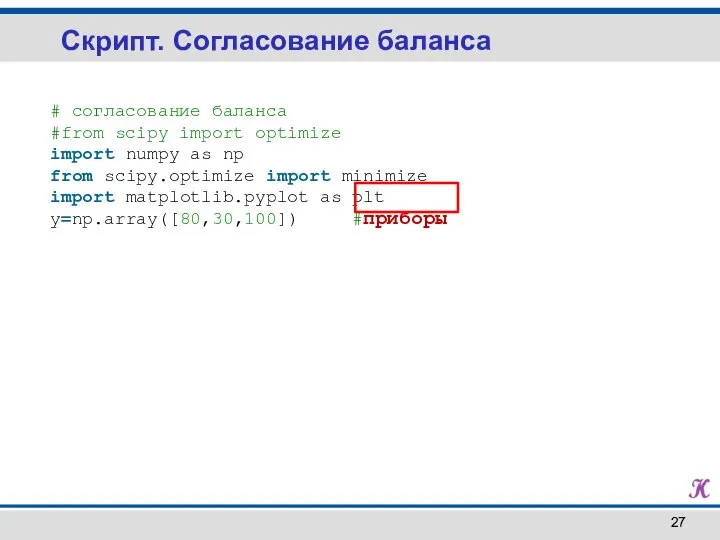
Скрипт. Согласование баланса
# согласование баланса
#from scipy import optimize
import numpy as np
from scipy.optimize import minimize
import matplotlib.pyplot as plt
y=np.array([80,30,100]) #приборы

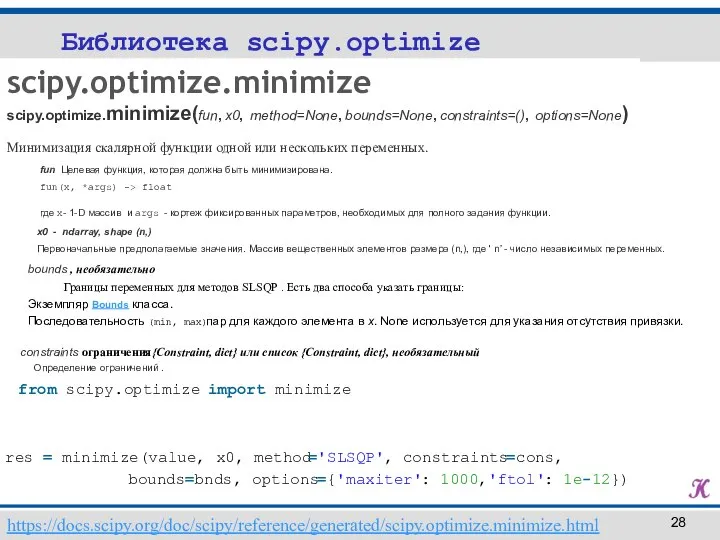
Библиотека scipy.optimize
scipy.optimize.minimize
scipy.optimize.minimize(fun, x0, method=None, bounds=None, constraints=(), options=None)
https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html
Минимизация скалярной функции одной или нескольких переменных.
fun Целевая функция, которая должна быть минимизирована.
fun(x, *args) -> float
где x- 1-D массив и args - кортеж фиксированных параметров, необходимых для полного задания функции.
x0 - ndarray, shape (n,)
Первоначальные предполагаемые значения. Массив вещественных элементов размера (n,), где ' n’ - число независимых переменных.
bounds , необязательно
Границы переменных для методов SLSQP . Есть два способа указать границы:
Экземпляр Bounds класса.
Последовательность (min, max)пар для каждого элемента в x. None используется для указания отсутствия привязки.
constraints ограничения{Constraint, dict} или список {Constraint, dict}, необязательный
Определение ограничений .
from scipy.optimize import minimize
res = minimize(value, x0, method='SLSQP', constraints=cons,
bounds=bnds, options={'maxiter': 1000,'ftol': 1e-12})

Метод SLSQP
minimize(method=’SLSQP’)
Метод SLSQP Sequential Least SQuares Programming использует Последовательное квадратичное программирование для минимизации функции нескольких переменных с любой комбинацией ограничений границ, равенства и неравенства .
Метод включает в себя подпрограмму оптимизации SLSQP, первоначально реализованную Дитером Крафтом (Kraft, D. A software package for sequential quadratic programming. 1988. Tech. Rep. DFVLR-FB 88-28, DLR German Aerospace Center – Institute for Flight Mechanics, Koln, Germany). Обратите внимание, что оболочка обрабатывает бесконечные значения в границах, преобразуя их в большие плавающие значения.

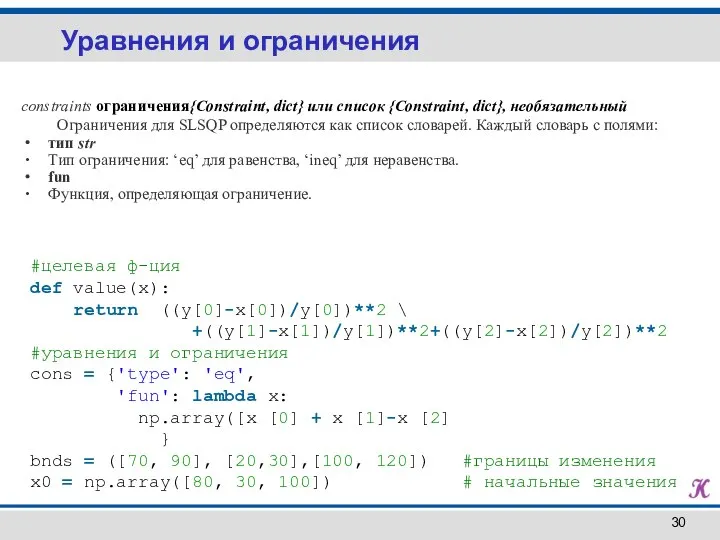
Уравнения и ограничения
constraints ограничения{Constraint, dict} или список {Constraint, dict}, необязательный
Ограничения для SLSQP определяются как список словарей. Каждый словарь с полями:
тип str
Тип ограничения: ‘eq’ для равенства, ‘ineq’ для неравенства.
fun
Функция, определяющая ограничение.
#целевая ф-ция
def value(x):
return ((y[0]-x[0])/y[0])**2 \
+((y[1]-x[1])/y[1])**2+((y[2]-x[2])/y[2])**2
#уравнения и ограничения
cons = {'type': 'eq',
'fun': lambda x:
np.array([x [0] + x [1]-x [2]
}
bnds = ([70, 90], [20,30],[100, 120]) #границы изменения
x0 = np.array([80, 30, 100]) # начальные значения

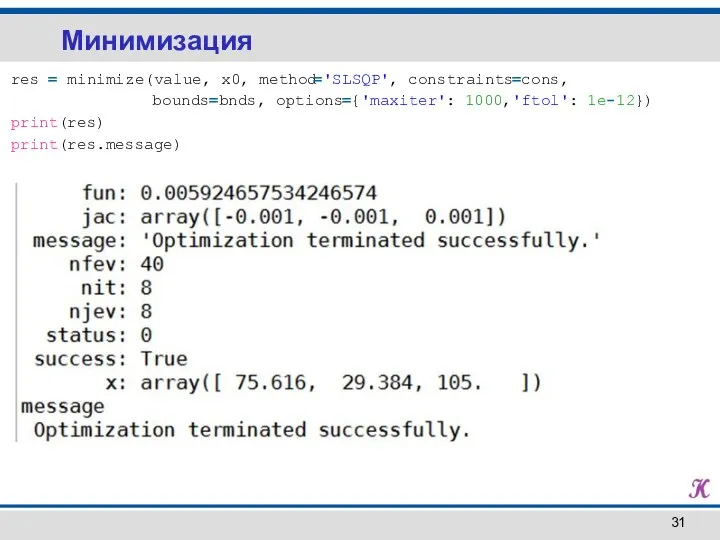
Минимизация
res = minimize(value, x0, method='SLSQP', constraints=cons,
bounds=bnds, options={'maxiter': 1000,'ftol': 1e-12})
print(res)
print(res.message)

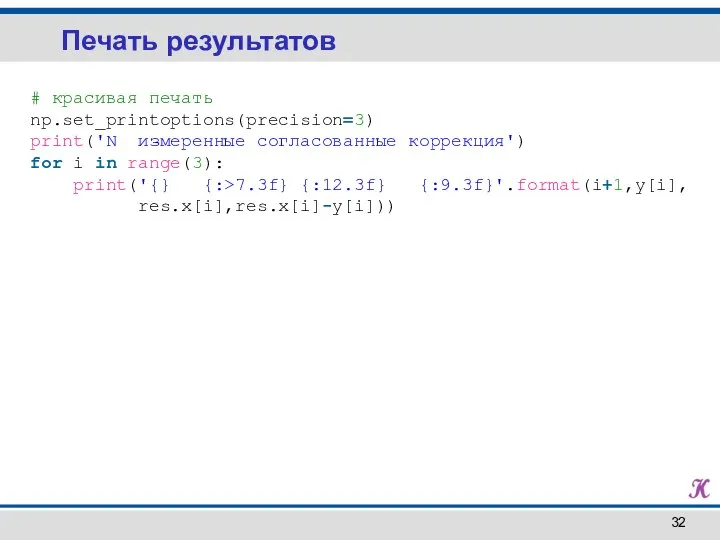
Печать результатов
# красивая печать
np.set_printoptions(precision=3)
print('N измеренные согласованные коррекция')
for i in range(3):
print('{} {:>7.3f} {:12.3f} {:9.3f}'.format(i+1,y[i],
res.x[i],res.x[i]-y[i]))

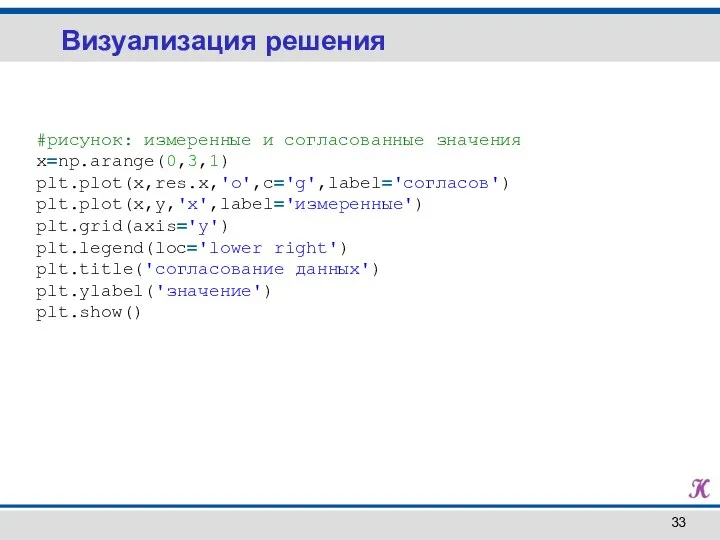
Визуализация решения
#рисунок: измеренные и согласованные значения
x=np.arange(0,3,1)
plt.plot(x,res.x,'o',c='g',label='сoгласов')
plt.plot(x,y,'x',label='измеренные')
plt.grid(axis='y')
plt.legend(loc='lower right')
plt.title('согласование данных')
plt.ylabel('значение')
plt.show()

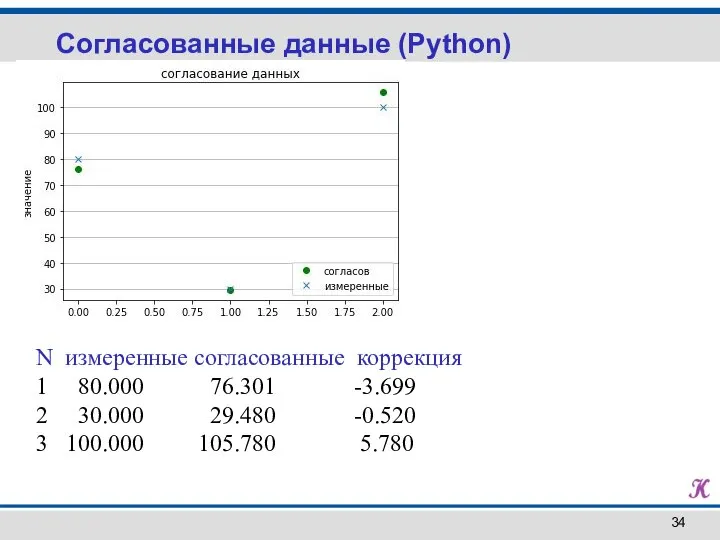
N измеренные согласованные коррекция
1 80.000 76.301 -3.699
2 30.000 29.480 -0.520
3 100.000 105.780 5.780
Согласованные данные (Python)

Проиллюстрировать работу алгоритма согласования данных на примере с одним узлом
На вход поступил 2 потока, измеренная масса за балансовый период
Вариант1 x01 =150 и x02 =40;
Вариант 2 x01 =150 и x02 =60;
на выходе x03 =200.
Для согласованных значений y выполняется закон сохранения масс и минимизируется целевая функция
Здесь - погрешности соответствующих измерений принять равной единице
Написать уравнение баланса
Вычислить согласованные значения с использованием Python
Ответить на вопрос «Имеются ли грубые ошибки измерения?» и обосновать свой ответ.
Задание 13_2 согласования данных с одним узлом

Инженерные приложения. Согласование данных

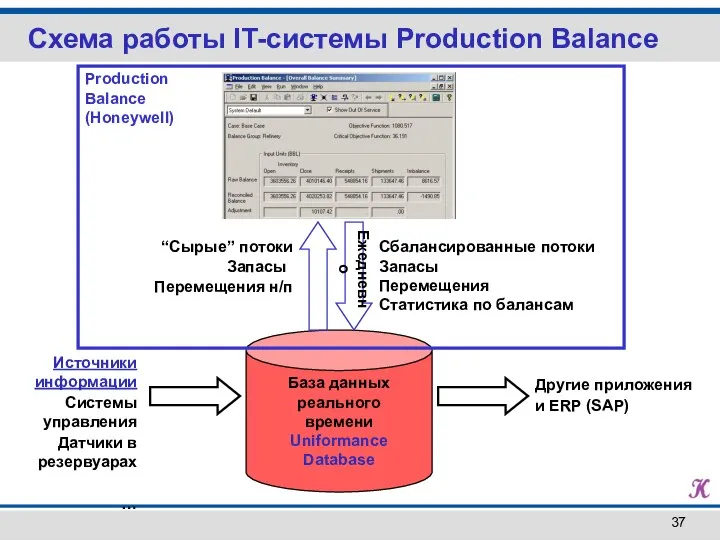
Схема работы IT-системы Production Balance
База данных реального
времени
Uniformance
Database
“Сырые” потоки
Запасы
Перемещения н/п
Ежедневно
Сбалансированные потоки
Запасы
Перемещения
Статистика по балансам
Другие приложения
и ERP (SAP)
Источники информации
Системы управления
Датчики в резервуарах
…
Production
Balance
(Honeywell)

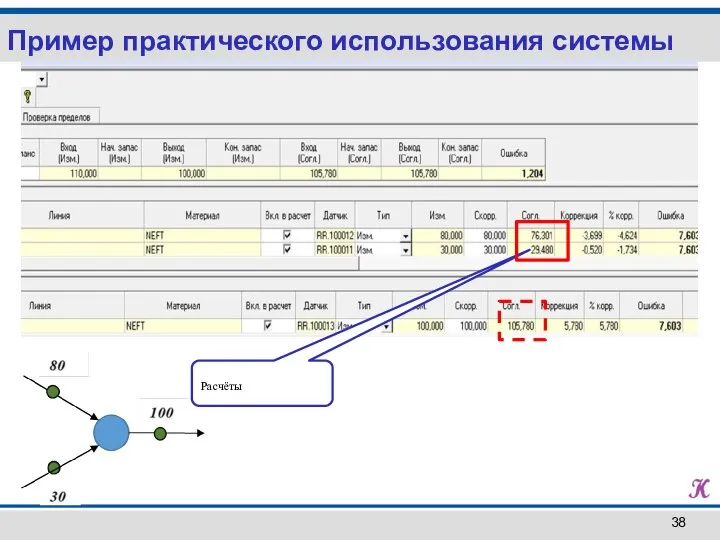
Пример практического использования системы
Расчёты

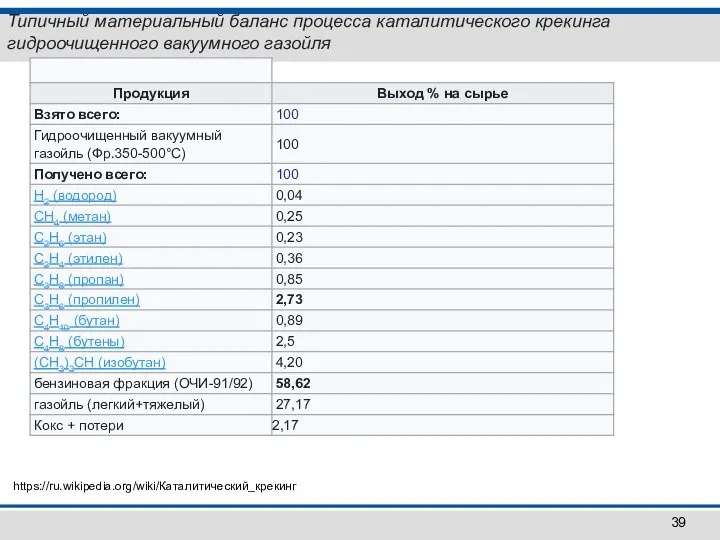
Типичный материальный баланс процесса каталитического крекинга гидроочищенного вакуумного газойля
https://ru.wikipedia.org/wiki/Каталитический_крекинг

SCALPELLUM Кувыкин В.И., Матвеев А.Е. и др. Свидетельство о регистрации программы для ЭВМ RUS 2015662513 13.10.2015
Инженерные приложения. Установка Каталитического Крекинга (УКК)

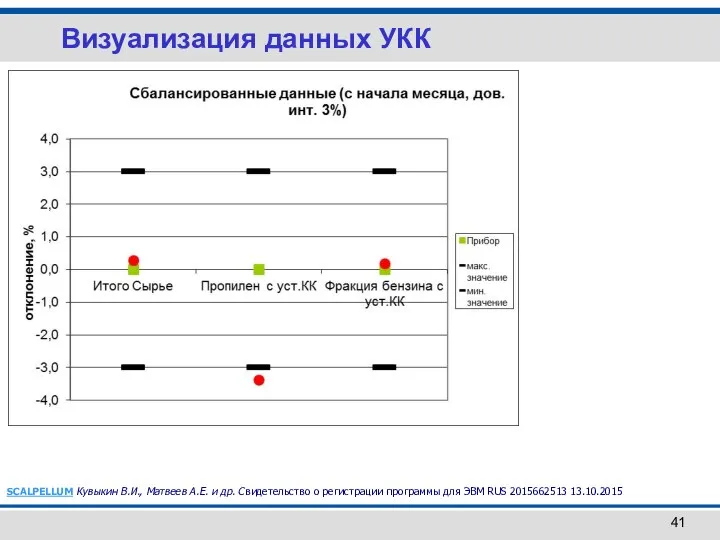
Визуализация данных УКК
SCALPELLUM Кувыкин В.И., Матвеев А.Е. и др. Свидетельство о регистрации программы для ЭВМ RUS 2015662513 13.10.2015

Вопросы ?