Квадратные уравнения

Автор: Бесфамильная Анна
ученица 8-а класса
Руководитель: Никифорова М.Н., учитель математики
ГОУ СОШ №1968
Москва
2010г.

Цели проекта:
Дать определение квадратного уравнения
Рассмотреть алгоритм решения квадратных уравнений
Познакомить с историей решения квадратных уравнений
Изучить теорему Виета
Найти занимательный материал по данной теме(кроссворды, стихи)

Определение квадратного уравнения.
Квадратным уравнением называется уравнение вида ах²+вх+с=0, где х – переменная, а,в,с – некоторые числа, причем а≠0.
Числа а, в, с – коэффициенты квадратного уравнения. Число а – первый коэффициент, в – второй коэффициент, с – свободный член.
Если в квадратном уравнении ах²+вх+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется неполным квадратным уравнением.
Квадратное уравнение, в котором коэффициент а=1 называется приведенным квадратным уравнением.

Стихотворение для запоминания формулы
«Пэ», со знаком взяв обратным,
На два мы его разделим.
И от корня аккуратно
Знаком минут-плюс отделим.
А под корнем, очень кстати,
Половина «пэ» в квадрате,
Минус «ку». И вот решенье
Небольшого уравненья.

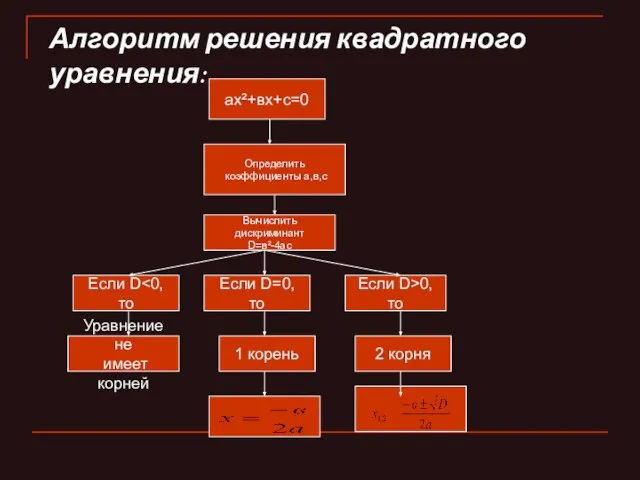
Алгоритм решения квадратного уравнения:

Кроссворд
1. Уравнение вида ах²+вх+с=о
2.Квадратные уравнения, у которых первый коэффициент равен 1.
3. Уравнения с одной переменной, имеющие одни и те же корни.
4. Числа а,в и с в квадратном уравнении.
5. Значение переменной, при котором уравнение обращается в верное равенство.
6. Равенство, содержащее неизвестное.
7. Неотрицательное значение квадратного корня.
8. Древнегреческий математик, который нашел приемы решения квадратных уравнений без обращения к геометрии.
9. Квадратное уравнение, в котором хотя бы один из коэффициентов в или с равен 0.
10. «Дискриминант» - по-латыни.
11. Коэффициент с квадратного уравнения.
12. Французский математик, который вывел формулы, выражающие зависимость корней уравнения от его коэффициентов.
Если вы разгадаете этот кроссворд верно, то сможете в выделенном вертикальном столбце прочитать термин, относящийся к теме.
К в а д р а т н о е
П р и в е д е н н о е
Р а в н о с и л ь н о е
К о э ф ф и ц и е н т
К о р е н ь
У р а в н е н и е
А р и ф м е т и ч е с к и й
Д и о ф а н т
Н е п о л н о е
Р а з л и ч и т е л ь
С в о б о д н ы й
В и е т

Из истории решения квадратных уравнений.
Уравнения 2-ой степени умели решать еще в Древнем Вавилоне во II тысячелетии до н.э. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид – при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактатах
Формула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте (около 598 г.).
Среднеазиатский ученый ал-Хорезми (IX в.) в трактате «Китаб аль-джебр валь -мукабала» получил эту формулу методом выделения полного квадрата с помощью геометрической интерпретации.

Уравнение с вещественными коэффициентами
Квадратное уравнение с вещественными коэффициентами a,b,c может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта D = b2 − 4ac:

при D > 0 корней два, и они вычисляются по формуле
при D = 0 корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях), кратности 2:
при D < 0 вещественных корней нет. Существуют два комплексных корня, выражающиеся той же формулой (1) (без использования извлечения корня из отрицательного числа), либо формулой

для нахождения корней можно использовать эквивалентное выражение
Вместо формулы
где k = b / 2. Это выражение является более удобным для практических вычислений при чётном b, то есть для уравнений вида ax² + 2kx + c = 0.

Квадратное уравнение вида x2 + px + q = 0, в котором старший коэффициент a равен единице, называют приведённым. В этом случае формула для корней
упрощается до

Мнемонические правила
«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
сводится всё к пустяку:
p пополам и в квадрате
Минус несчастное прекрасное q.

Уравнение с комплексными коэффициентами
В комплексном случае квадратное уравнение решается по той же формуле
и указанным выше ее вариантам, но различимыми является только два случая: нулевого дискриминанта (один корень) и ненулевого (два корня).

По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни - и дробь уж готова:
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь - это что за беда -
В числителе в, в знаменателе а.
Теорема Виета

Теорема Виета
Сумма корней приведённого квадратного уравнения x² + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q:
В общем случае (для неприведённого квадратного уравнения ax² + bx + c = 0):

Разложение квадратного уравнения на множители
Если известны оба корня квадратного уравнения, его можно разложить по формуле
В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

Уравнения, сводящиеся к квадратным
Уравнение вида
является уравнением, сводящимся к квадратному.
В общем случае оно решается заменой
c последующим решением квадратного уравнения
Также при решении можно обойтись без замены, решив совокупность двух уравнений
и
Если f (x) = x², то уравнение принимает вид:
ax^4 + bx² + c = 0
Такое уравнение называется биквадратным

Выводы:
1 В процессе работы над презентацией я изучила решение квадратных уравнений.
2 Научилась пользоваться формулами для решения квадратных уравнений
3 Узнала об истории решения
4 Данная презентация будет полезна учащимся 8-9классов для изучения и повторения при решении квадратных уравнений
5 Презентация окажет помощь учителям при объяснении темы «Квадратные уравнения»