Содержание
- 2. Операция: A, B, C, … или A1, A2, A3, … параметры операции: Aij, Aijk, … или
- 3. Пример составления ЛСА: Алгоритм Евклида нахождения общего делителя для натуральных чисел a и b. Операторы и
- 4. Пример: Ap↑1q↑2↑3C↓2BDp↑1q↑2ω↑3↓10 aAi ↓ если p=q=1, то aAC=pq если p=1, а q=0, то aAB=pq если p=0,
- 6. Скачать презентацию
Слайд 2Операция:
A, B, C, …
или
A1, A2, A3, …
параметры операции:
Aij, Aijk, …
или
A(ij), A(ijk), …
Запись
Операция:
A, B, C, …
или
A1, A2, A3, …
параметры операции:
Aij, Aijk, …
или
A(ij), A(ijk), …
Запись

операторов:
линейный алгоритм
разветвленный алгоритм:
логические условия – p, q, r, …
p[f(x1, x2, …, xn)]
ω – тождественно-ложные логические условия
У каждого ЛУ есть ↑(или ↓):
↑i – начало i-ой стрелки (справа от ЛУ)
↓i – конец i-ой стрелки (слева от ЛУ=0)
ЛСА
линейный алгоритм
разветвленный алгоритм:
логические условия – p, q, r, …
p[f(x1, x2, …, xn)]
ω – тождественно-ложные логические условия
У каждого ЛУ есть ↑(или ↓):
↑i – начало i-ой стрелки (справа от ЛУ)
↓i – конец i-ой стрелки (слева от ЛУ=0)
ЛСА
Пример:
↓2Аp1↑1B↓1p2↑2C
Выполнение ЛСА:
если p1=p2=0, то – АА…А…
если p1=0, p2=1, то – АС
если p1=1, p2=0, то – АВАВ…АВ
если p1=1, p2=1, то – АВС
Пример:
А↓1Вp↑2Сω↑1↓2D
Выполнение ЛСА:
ABCBC…BC…BC BD
p=1 p=0
Слайд 3Пример составления ЛСА:
Алгоритм Евклида нахождения общего делителя для натуральных чисел a и
Пример составления ЛСА:
Алгоритм Евклида нахождения общего делителя для натуральных чисел a и

b.
Операторы и ЛУ:
А
В – х у
С – х и у
D
O
p – x и y
p=1 – x=y
p=0 – x≠y
q = x>y
q=1 – x>y
q=0 – xAp↑1q↑2↑3C↓2BDp↑1q↑2ω↑3↓10
A0
Ak
Операторы и ЛУ:
А
В – х у
С – х и у
D
O
p – x и y
p=1 – x=y
p=0 – x≠y
q = x>y
q=1 – x>y
q=0 – x
A0
Ak
Матричные схемы алгоритмов и их связь с логическими схемами. Понятие о граф-схемах.
aij
Aj – j-ый столбец
Ai – i-ая строка
если aij=aij(p1, …, pm)=1
Свойства ЛФ МСА:
aijaij=0, i≠j;
k
Vaij=1
j=1
Слайд 4Пример:
Ap↑1q↑2↑3C↓2BDp↑1q↑2ω↑3↓10
aAi
↓
если p=q=1, то aAC=pq
если p=1, а q=0, то aAB=pq
если p=0, то aAO=p
aAD=0
aCB=1
Переход
Пример:
Ap↑1q↑2↑3C↓2BDp↑1q↑2ω↑3↓10
aAi
↓
если p=q=1, то aAC=pq
если p=1, а q=0, то aAB=pq
если p=0, то aAO=p
aAD=0
aCB=1
Переход

от МСА к ЛСА с использованием формул перехода.
C→B
aij
Aj
A→pqC V pqB V pO
Система формул перехода:
A→pqC V pqB V pO
C→B
B→D
D→pqC V pqB V pO
A0
Ap↑q↑
Ap↑q↑C
Ap↑q↑CB
Ap↑q↑CBD
Ap↑q↑↓1CBDp↑q↑ω↑1
C→B
aij
Aj
A→pqC V pqB V pO
Система формул перехода:
A→pqC V pqB V pO
C→B
B→D
D→pqC V pqB V pO
A0
Ap↑q↑
Ap↑q↑C
Ap↑q↑CB
Ap↑q↑CBD
Ap↑q↑↓1CBDp↑q↑ω↑1
- Предыдущая
Описание и преобразование управляющих процессов Следующая -
Лечение артериальной гипертензии  Направления альтернативной энергетики
Направления альтернативной энергетики Графические работы. Черчение и перспектива
Графические работы. Черчение и перспектива Презентация на тему Клетка:история изучения Клеточная теория
Презентация на тему Клетка:история изучения Клеточная теория  Moodle
Moodle Группа 19 САТ 1,2
Группа 19 САТ 1,2 Продажа земельного участка Ломоносовский район Низинское сельское поселение дер. Троицкая гора, уч. №2/1
Продажа земельного участка Ломоносовский район Низинское сельское поселение дер. Троицкая гора, уч. №2/1 Информационно-технологическое обеспечение проведения государственной (итоговой) аттестации выпускников IX классов общеобразоват
Информационно-технологическое обеспечение проведения государственной (итоговой) аттестации выпускников IX классов общеобразоват Snezhok (1)
Snezhok (1) Психология малых групп
Психология малых групп Проблема травматизма в последние годы становится актуальной для всех регионов. Особую тревогу вызывает увеличение высокоэнергет
Проблема травматизма в последние годы становится актуальной для всех регионов. Особую тревогу вызывает увеличение высокоэнергет Владимир Григорьевич Сутеев
Владимир Григорьевич Сутеев Презентация на тему Основные формы рельефа суши
Презентация на тему Основные формы рельефа суши Презентация на тему Украина в годы Второй Мировой войны
Презентация на тему Украина в годы Второй Мировой войны 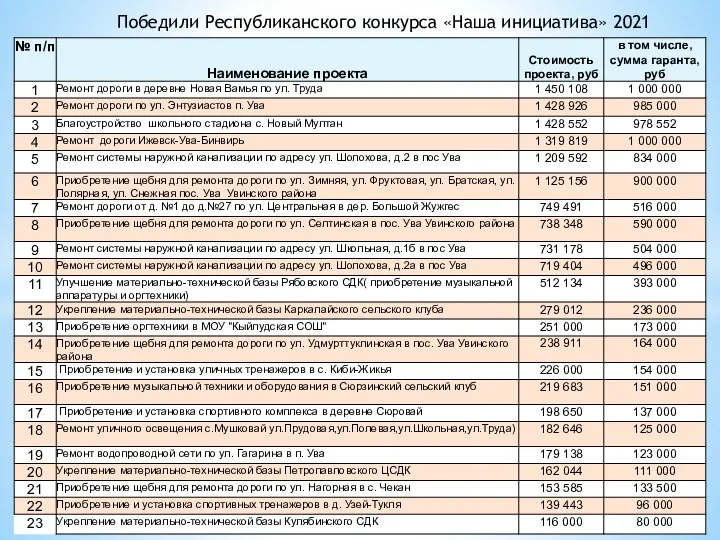 Ремонты дорог
Ремонты дорог ВКР: Особенности работы банков с проблемными кредитами: российский и зарубежный опыт
ВКР: Особенности работы банков с проблемными кредитами: российский и зарубежный опыт Программирование компьютерной графики
Программирование компьютерной графики Александр Матросов
Александр Матросов Проект Время спорту
Проект Время спорту Коммерческое предложение по билбордам и призмаборда 2018 года
Коммерческое предложение по билбордам и призмаборда 2018 года По литературным местам Гаврилов-Ямского района
По литературным местам Гаврилов-Ямского района Уличные газовые инфракрасные обогреватели
Уличные газовые инфракрасные обогреватели Объект
Объект Программирование в компьютерных системах (230115)
Программирование в компьютерных системах (230115) Рахманкулова Лейсан
Рахманкулова Лейсан Презентация на тему Зимний дворец
Презентация на тему Зимний дворец 9 0 0 дней с 8 сентября 1941 года по 27 января 1944 года
9 0 0 дней с 8 сентября 1941 года по 27 января 1944 года ХРАМОВАЯ АРХИТЕКТУРА ИНДЕЙЦЕВ МЕСАМЕРИКИ КАК ВОПЛОЩЕНИЕ МИФА О ЖЕРТВЕ, ДАВШЕЙ ЖИЗНЬ Пирамида Солнца в Теотиуакане. Храм бога Уици
ХРАМОВАЯ АРХИТЕКТУРА ИНДЕЙЦЕВ МЕСАМЕРИКИ КАК ВОПЛОЩЕНИЕ МИФА О ЖЕРТВЕ, ДАВШЕЙ ЖИЗНЬ Пирамида Солнца в Теотиуакане. Храм бога Уици