Содержание
- 2. Choosing independent variables Three popular methods of choosing independent variables are: Hellwig's method Graphs analysis method
- 3. Hellwig’s method Three steps: Number of combinations: 2m-1 Individual capacity of every independent variable in the
- 4. Hellwig’s method 1. Number of combinations In Hellwig’s method the number of combinations is provided by
- 5. Hellwig’s method 2. Individual capacity of each independent variable in the combination is given by the
- 6. Hellwig’s method 2. Individual capacity of each independent variable in the combination is given by the
- 7. Hellwig’s method 2. Individual capacity of each independent variable in the combination is given by the
- 8. Hellwig’s method 2. Individual capacity of each independent variable in the combination is given by the
- 9. Hellwig’s method 3. Integral capacity of information for every combination The next step is to calculate
- 10. Hellwig’s method Q: HOW TO CHOOSE INDEPENDENT VARIABLES? A: LOOK AT INTEGRAL CAPACITIES OF INFORMATION. THE
- 11. Example Let’s choose independent variables, using Hellwig's method.
- 12. Example First we need to have vector and matrix of correlation coefficients. ❑ Correlation coefficients between
- 13. Example First we need to have vector and matrix of correlation coefficients. ❑ Correlation matrix R
- 14. Example 1. Number of combinations We have 3 independent variables X1, X2 and X3. Thus we
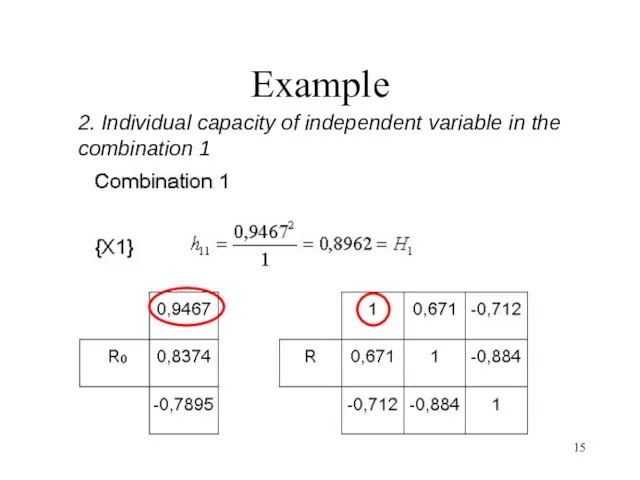
- 15. Example 2. Individual capacity of independent variable in the combination 1
- 16. Example 2. Individual capacity of independent variable in the combination 2
- 17. Example 2. Individual capacity of independent variable in the combination 3
- 18. Example 2. Individual capacity of every independent variable in the combination 4
- 19. Example 2. Individual capacity of independent variables in the combination 5
- 20. Example 2. Individual capacity of every independent variables in the combination 6
- 21. Example
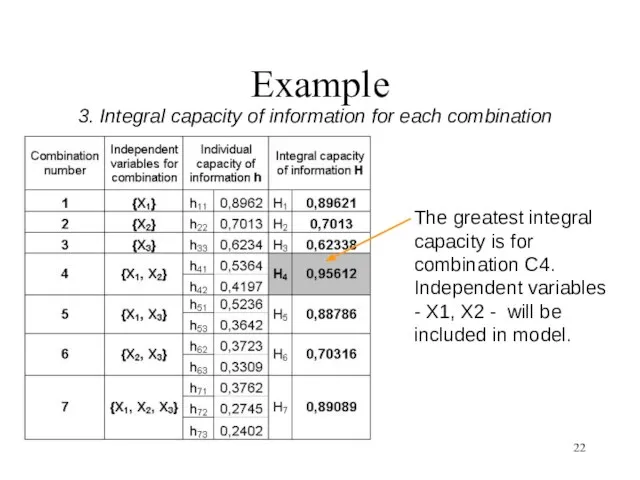
- 22. Example 3. Integral capacity of information for each combination The greatest integral capacity is for combination
- 23. Graph analysis method Three steps Calculating r* Modification of correlation matrix Drawing the graph
- 24. Graph analysis method Q: HOW TO CHOOSE INDEPENDENT VARIABLES? A: LOOK AT THE GRAPHS. THE NUMBER
- 25. Graph analysis method Calculating r* We start with calculating critical value of r* using the formula:
- 26. Graph analysis method 2. Modification of correlation matrix The correlation coefficients for which are statistically irrelevant
- 27. Example Let’s have an example (the same one as for Hellwig’s method, n=7)
- 28. Example 1. Calculating r* (n=7, tα, n-2=t0,05,5=2,571)
- 29. Example Modification of correlation matrix
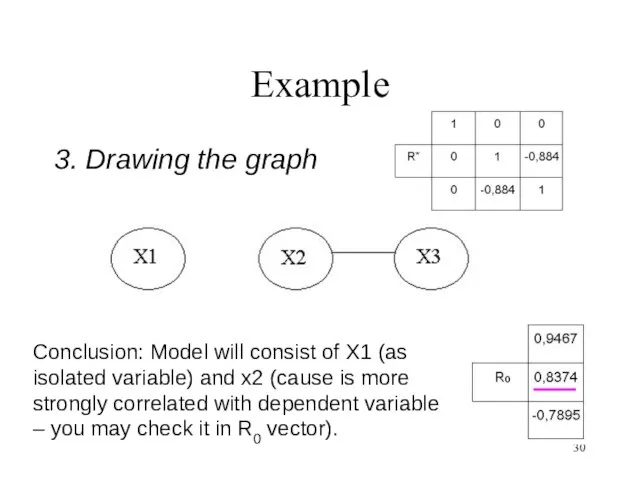
- 30. Example 3. Drawing the graph Conclusion: Model will consist of X1 (as isolated variable) and x2
- 31. Correlation matrix method Calculate r* We start with calculating critical value of r* using the formula:
- 32. 2. To eliminate Xi variables weakly correlated withY 3. To choose Xs where [Xs is the
- 33. Example Let’s have an example (the same one as for Hellwig’s method and graph analysis metod,
- 34. Example 1. Calculating r* (n=7, tα, n-2=t0,05,5=2,571)
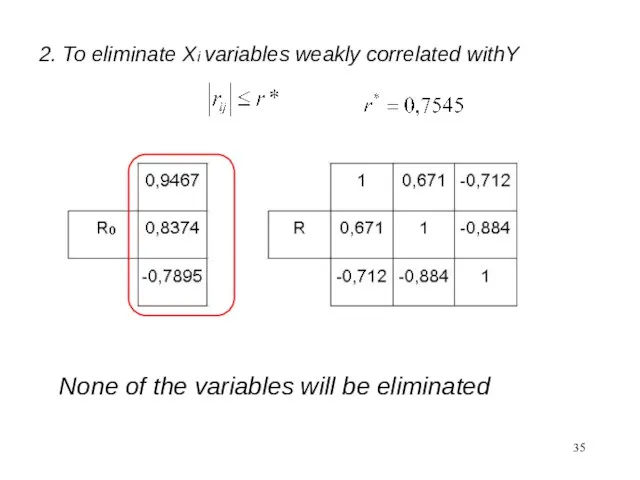
- 35. 2. To eliminate Xi variables weakly correlated withY None of the variables will be eliminated
- 36. 3. To choose Xs where
- 37. 4. To eliminate Xi variables strongly correlated with Xs None of the variables will be eliminated.
- 39. Скачать презентацию



























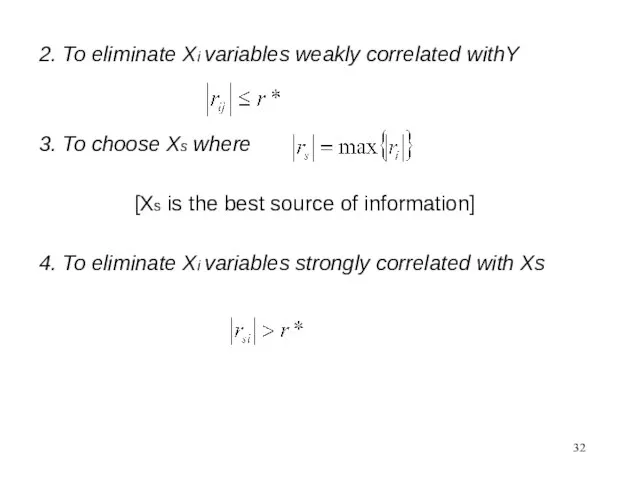




 Рождество – день особый, поверьте
Рождество – день особый, поверьте От опорных конспектов – к алгоритмизации и компьютеризации
От опорных конспектов – к алгоритмизации и компьютеризации Развитие умение писать глаголы с изученными орфограммами
Развитие умение писать глаголы с изученными орфограммами Что видит «Лондонский глаз»?
Что видит «Лондонский глаз»? Олимпийские надежды Свислоччины
Олимпийские надежды Свислоччины Метрологическое сопровождение в рамках новых строящихся объектов производств и комплексов
Метрологическое сопровождение в рамках новых строящихся объектов производств и комплексов Инновационные процессы в образовании
Инновационные процессы в образовании Внебюджетные фонды. Тема 6
Внебюджетные фонды. Тема 6 Клавиатура
Клавиатура Оформлення виплат, пов’язаних з оплатою праці, стипендій, премій та інших виплат за платіжними відомостями
Оформлення виплат, пов’язаних з оплатою праці, стипендій, премій та інших виплат за платіжними відомостями «Жемчужина России-Байкал»
«Жемчужина России-Байкал» «А Р М И Н Ж Е Н Е Р А И П Л»
«А Р М И Н Ж Е Н Е Р А И П Л» SUDUDU
SUDUDU Приобретение гражданства Российской Федерации
Приобретение гражданства Российской Федерации Смычковые инструменты
Смычковые инструменты Культура средневековой Индии
Культура средневековой Индии Моя будущая профессия. Составитель поездов
Моя будущая профессия. Составитель поездов Пейнтбольная площадка в Юрмале
Пейнтбольная площадка в Юрмале Лучшие знатоки русского языка
Лучшие знатоки русского языка Политические режимы
Политические режимы Презентация на тему Волго–Вятский экономический район
Презентация на тему Волго–Вятский экономический район  Гимнастика в 5-11 классах
Гимнастика в 5-11 классах Make up for ever
Make up for ever Построение матрицы ответственности IT-проекта
Построение матрицы ответственности IT-проекта Прямоугольник и квадрат
Прямоугольник и квадрат Антология современной русской литературы
Антология современной русской литературы Оружие массового поражения и защита от него
Оружие массового поражения и защита от него Значение воды в жизнедеятельности живых организмов
Значение воды в жизнедеятельности живых организмов