Лекции по физике. Механика

Механические колебания
Колебаниями называются процессы, происходящие с некоторой долей повторяемости
Классификация колебаний
Свободные (собственные)
Вынужденные
Параметрические
Автоколебания

Механические колебания
Гармонические колебания описываются гармоническими функциями (sin, cos)
Процессы в природе часто близки к гармоническим
Любые колебания можно рассматривать как суперпозицию гармонических

Малые колебания
Рассмотрим механическую систему с одной степенью свободы, имеющую минимум потенциальной энергии U(x) в точке x=0
Разложим U(x) в ряд Маклорена:
U(x)=U(0)+U′(0)⋅x+1/2⋅U″(0)⋅x2+…
из условия минимума → U′(0)=0 и U″(0)>0
положим U(0)=0 → U(x)=1/2⋅k ⋅x2

Малые колебания
F=-gradU=-k⋅x – восстанавливающая сила
Если эта сила действует на тело массой m, то уравнение движения принимает вид:
m⋅x″=-k⋅x или x″+k/m⋅x=0
Решение этого уравнения:
x=A⋅cos(ω0⋅t+ϕ0), ω02=k/m,
где A – амплитуда, ϕ0 – начальная фаза,
ω0 – круговая частота, ω0⋅t+ϕ0 – фаза

Малые колебания
Сила трения: Fтр=-r⋅x′, где r – коэффициент сопротивления
Уравнение движения с учётом силы трения:
m⋅x″=-k⋅x-r⋅x′ или x″+2⋅β⋅x′+ ω02⋅x=0,
где 2⋅β=r/m>0.
Это уравнение описывает затухающие собственные колебания

Малые колебания
Решение уравнения:
x=A⋅e-β⋅t⋅cos(ω⋅t+ϕ0),
При действии на систему внешней силы f(t) уравнение движения принимает вид:
x″+2⋅β⋅x′+ ω02⋅x=f(t) (1)
Это уравнение описывает вынужденные колебания. Решение будет гармоническим, если f(t) – гармоническая функция: f(t)=F0⋅cos(ω⋅t)
В общем случае ω≠ω0

Малые колебания
Уравнение (1) является линейным дифференциальным уравнением второго порядка с постоянными коэффициентами
Если f(t)≠0, то (1) неоднородное уравнение, если f(t)=0, то однородное
Общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и какого-либо частного решения неоднородного уравнения

Малые колебания
При f(t)=F0⋅cos(ω⋅t) решение уравнения (1) имеет вид:

Малые колебания
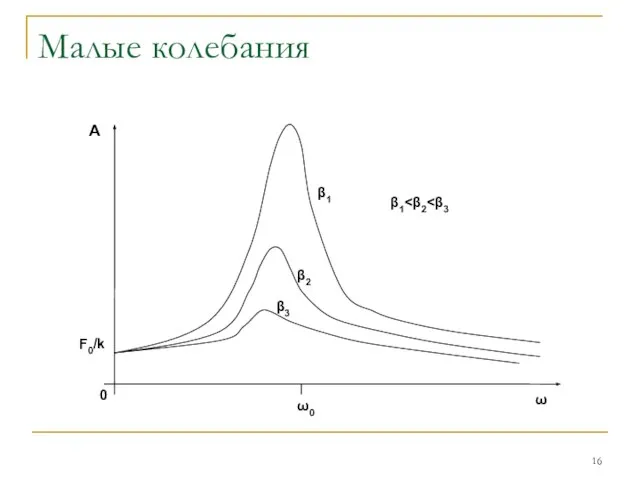
Особенности решения:
Частота колебаний равна частоте вынуждающей силы
При ω→ω0 наступает явление резонанса при котором амплитуда вынужденных колебаний достигает максимума
Вынужденные колебания отстают по фазе от вынуждающей силы
Угол отставания ϕ=π/2 при резонансной частоте, ϕ→0 при ω→0 и ϕ→π при ω→∞

Явление резонанса

Малые колебания

Гармонические колебания
x=A⋅cos(ω0⋅t+ϕ0)
Период: T=2⋅π/ω0, c
Частота: ν=1/T=ω0/2⋅π, Гц
Скорость: v=x′=-A⋅ω0 ⋅sin(ω0⋅t+ϕ0)=
= A⋅ω0 ⋅cos(ω0⋅t+ϕ0+π/2)
Ускорение: a=x″=-A⋅ω02 ⋅cos(ω0⋅t+ϕ0)=
= A⋅ω02 ⋅cos(ω0⋅t+ϕ0+π)=

Гармонические колебания
Значения A и ϕ0 могут быть определены из начальных условий, т.к. при t=0:
x0=A⋅cos(ϕ0), v0=-A⋅ω0⋅sin(ϕ0)
Отсюда получаем:

Гармонические колебания
В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно. Кинетическая энергия достигает максимума при прохождении точки равновесия, а потенциальная – в точках максимального отклонения

Сложение колебаний
Согласно теореме Фурье негармоническое колебание можно представить как бесконечную сумму гармонических колебаний с частотами кратными частоте исходного колебания:

Пружинный маятник
Возвращающая сила:
Fн=k⋅Δl
Уравнение движения:
Δl″+(k/m)⋅Δl=0
Частота и период колебаний:

Математический маятник
Положение системы задаётся углом отклонения.
Уравнение движения:
m⋅l2⋅ϕ″=-m⋅g⋅l⋅ϕ или ϕ″+(g/l)⋅ϕ=0
Частота и период колебаний:

Гармонические колебания
Широкое применение на практике получили генераторы колебаний – устройства в которых возбуждаются и поддерживаются автоколебания. В этих устройствах потери энергии колебательной системы компенсируются за счёт подвода энергии извне с помощью специального механизма

Звуковые колебания
Особую роль в жизни людей играют звуковые колебания которые представляют собой колебания частиц окружающей среды (воздух, вода и т.д.). Эти колебания используются для получения информации об окружающем мире
Существуют различные способы возбуждения звуковых колебаний