Содержание
- 2. Представление гармонических колебаний и монохроматических волн в комплексном виде
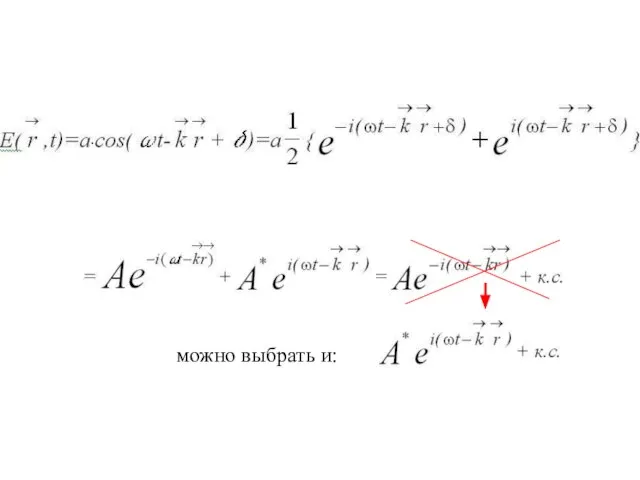
- 4. можно выбрать и:
- 5. Комплексная амплитуда у скалярной волны означает наличие начальной фазы и медленно-меняющейся фазы. Комплексное число + комплексно
- 6. Для всех линейных операций (суммирование, интегрирование, вычитание, дифференцирование, использование граничных условий и т. д., но не
- 7. т.е. вместо действительного выражения использовать комплексную запись для поля E( ,t)
- 8. Достоинство комплексного представления колебательных и волновых процессов состоит в простоте обращения с показательной функцией по сравнению
- 9. Если в конечном результате отделить действительную часть (удвоив амплитуду) от мнимой, то получится тот же результат,
- 10. Векторный характер электромагнитных волн ( векторные волны )
- 11. Поскольку напряженность электрического поля - величина векторная, то и ЭМВ - величина векторная.
- 12. Если - вещественная величина, то это уравнение плоской монохроматической линейно поляризованной волны. Если -комплексная, то поляризация
- 13. Математическое отступление
- 14. Вектор в прямоугольной системе координат
- 15. скалярное произведение векторов
- 16. векторное произведение
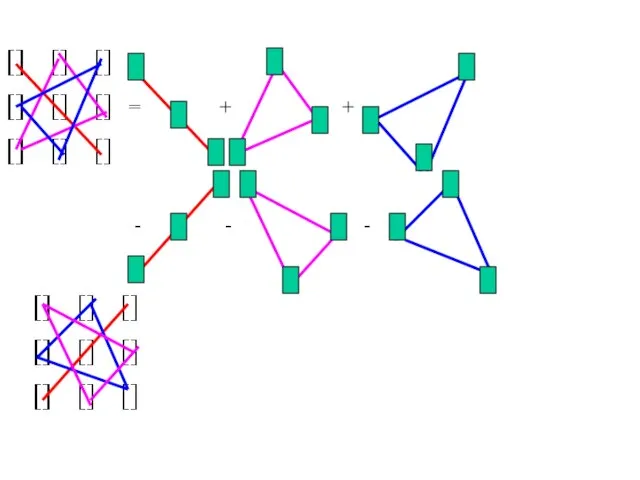
- 17. Определитель матрицы 3x3
- 18. = + + - - -
- 19. Ротор
- 20. Дивергенция
- 21. Градиент
- 22. Поперечность ЭМВ. Ортогональность и
- 23. Рассмотрим плоские волны в диэлектрике:
- 24. Уравнение Максвелла для плоских волн:
- 25. Уравнение Максвелла для плоских волн:
- 27. т.к. и т.д.
- 28. Таким образом и а
- 29. Уравнения Максвелла имеют вид:
- 30. Уравнения Максвелла имеют вид:
- 31. Уравнения Максвелла имеют вид:
- 32. Отсюда следует, что и ,
- 33. т.е. перпендикулярны направлению распространения волны и , Таким образом, ЭМВ - волны поперечные.
- 34. Итак, взаимно перпендикулярные векторы. образуют правовинтовую систему.
- 35. образуют правовинтовую систему.
- 36. , т.е. отношение численных значений векторов от времени не зависит, т.е. эти векторы обладают одинаковыми фазами.
- 37. В бегущей ЭМВ векторы и изменяются синхронно.
- 38. Энергия, переносимая ЭМВ
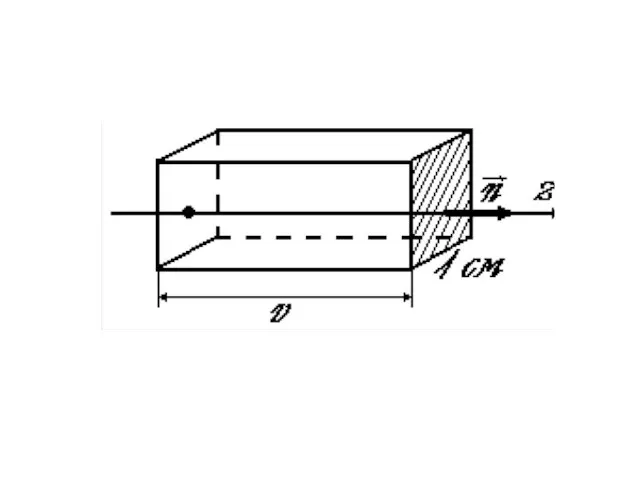
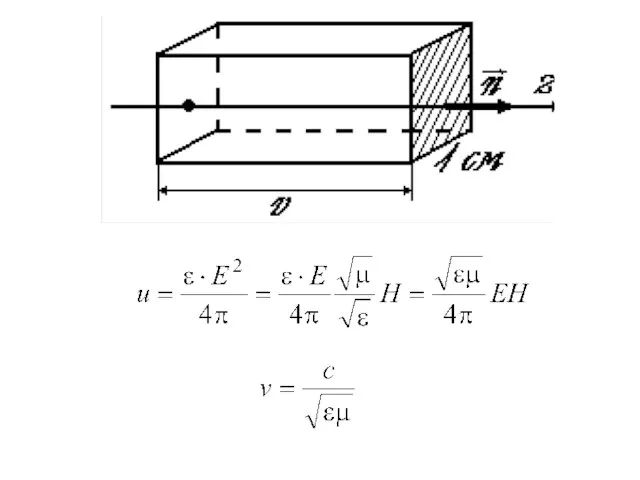
- 39. Найдем количество энергии, которое протекает в 1 сек через площадку в 1 см, которая перпендикулярна направлению
- 40. Тогда количество энергии, которое протекает через основание параллелепипеда (цилиндра) в 1 сек, равно энергии содержащейся в
- 42. Следовательно, поток энергии , где плотность энергии (энергия в единице объёма).
- 45. Вектор Умова-Пойтинга совпадает с только в изотропной среде
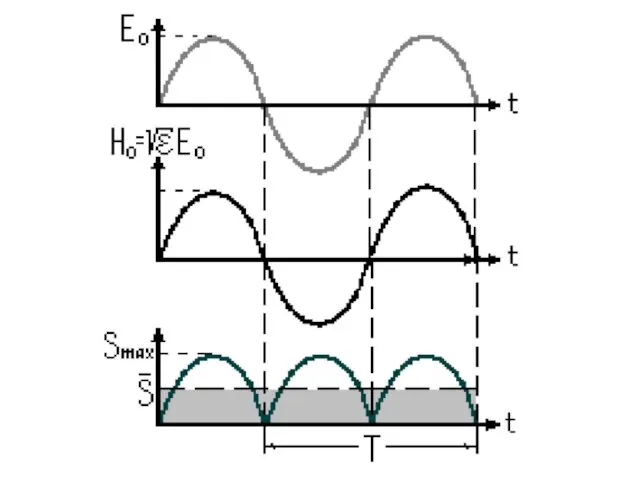
- 46. Вектор Умова-Пойтинга изменяется от значения до
- 47. Таким образом, поток энергии колеблется с удвоенной частотой по сравнению с и около среднего значения
- 48. принимая положительные значения (включая ).
- 50. Поток энергии пропорционален квадрату амплитуды поля ЭМВ. Это общее и очень важное соотношение, на котором фактически
- 51. Поэтому они регистрируют среднее значение квадрата амплитуды поля (квадратичный детектор).
- 52. Световое давление
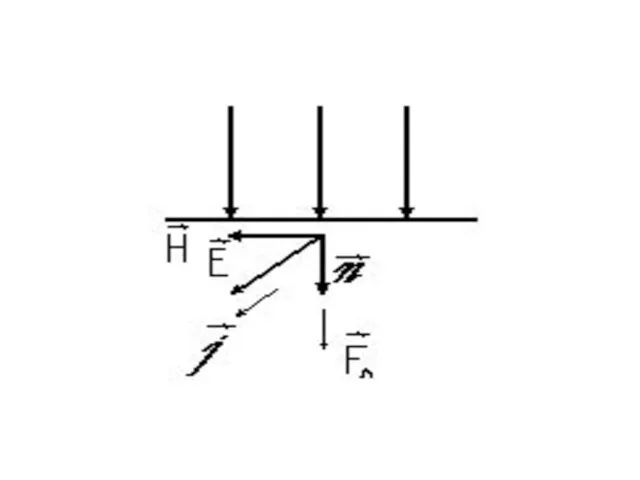
- 53. Поскольку свет электромагнитная поперечная волна, то падая на поверхность проводника (зеркально отражающего или поглощающего тела), он
- 55. магнитное поле световой волны действует на возникший ток по закону Ампера (сила Лоренца) так, что направление
- 57. Таким образом, взаимодействие между светом и отражающим или поглощающим его телом приводит к возникновению давления на
- 58. Для случая, когда световые лучи образуют параллельный пучок, давление p по вычислению Максвелла равняется плотности световой
- 59. Если часть энергии отражается, то давление увеличивается в раз, так как при отражении света, вектор снова
- 60. где R − коэффициент отражения тела, для идеального зеркала R=1 p=2u
- 61. Примеры: 1. Для силы, с которой солнечные лучи в яркий день давят на чёрной поверхности, Максвелл
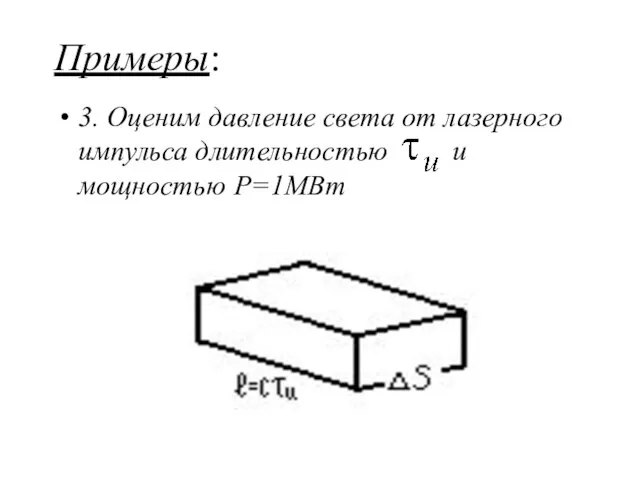
- 62. Примеры: 3. Оценим давление света от лазерного импульса длительностью и мощностью Р=1МВт
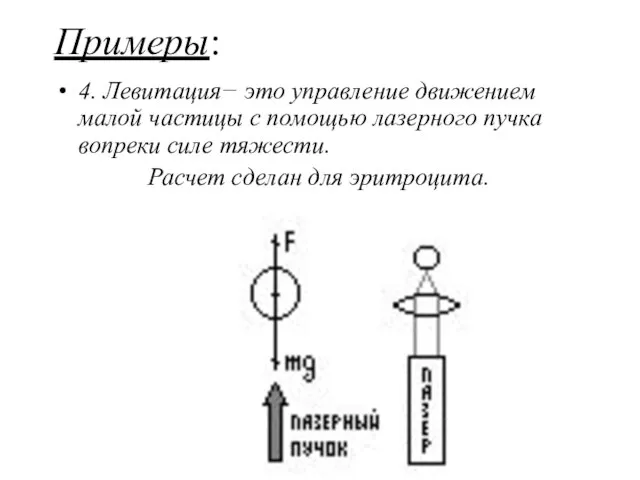
- 64. Примеры: 4. Левитация− это управление движением малой частицы с помощью лазерного пучка вопреки силе тяжести. Расчет
- 67. Скачать презентацию

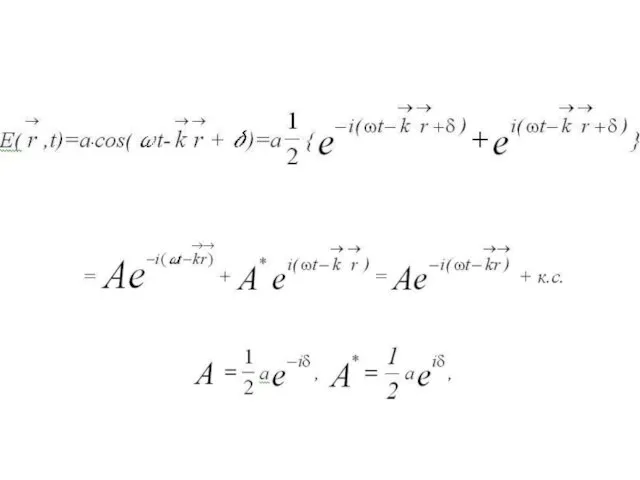






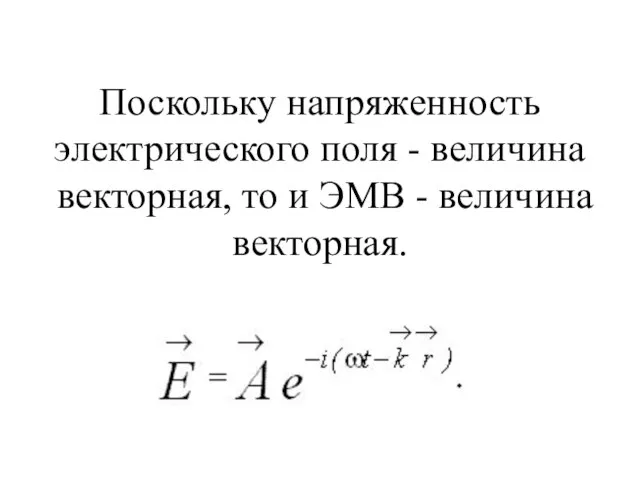






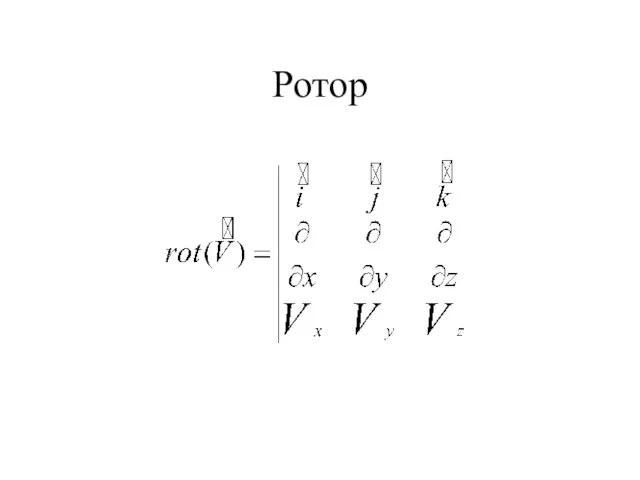
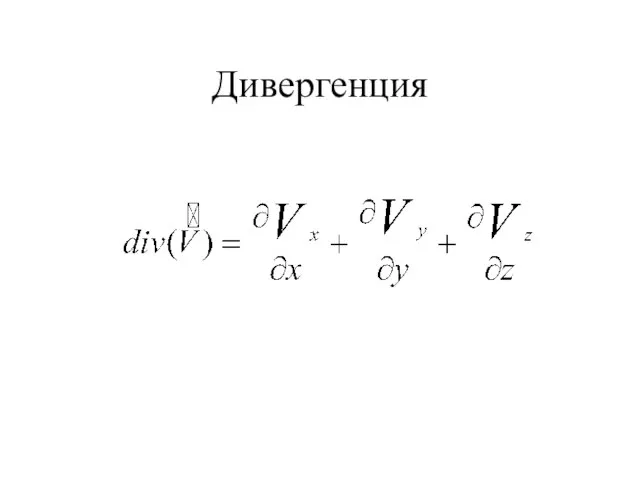
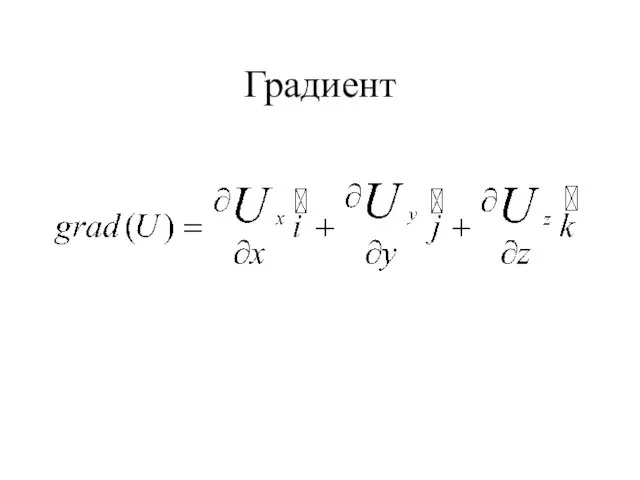




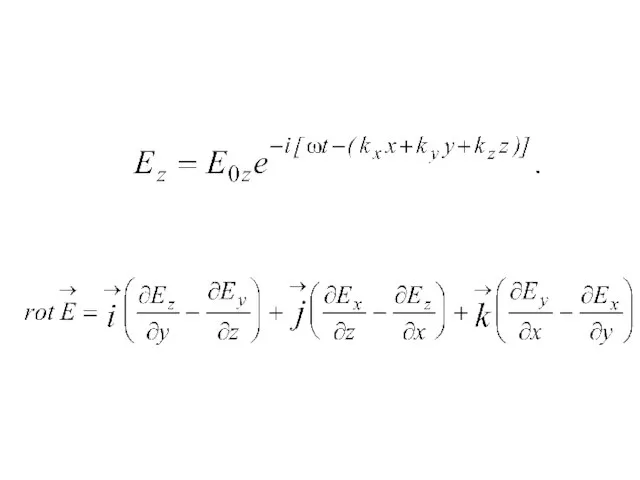
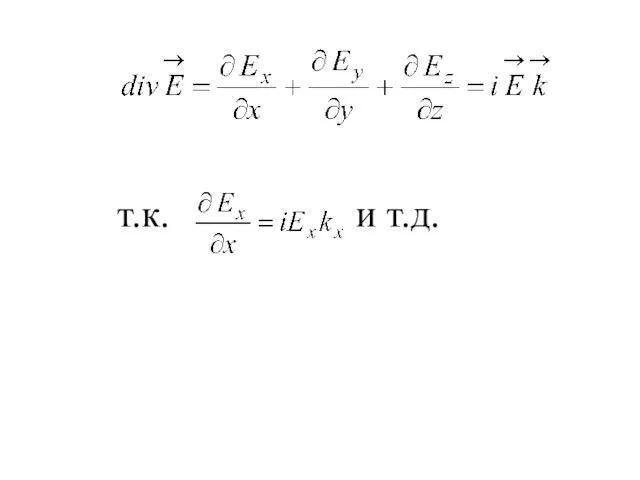
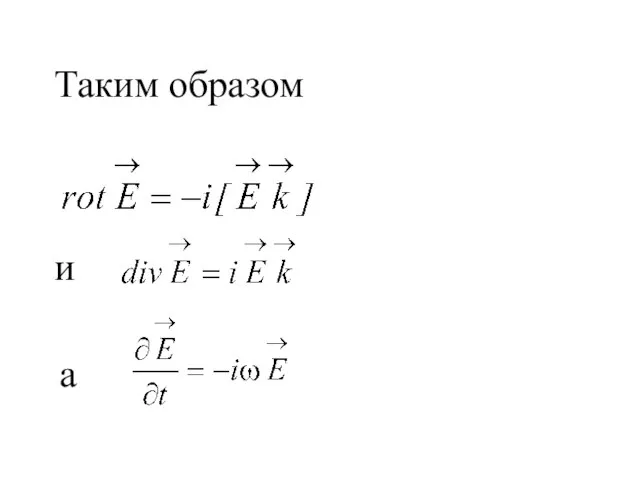



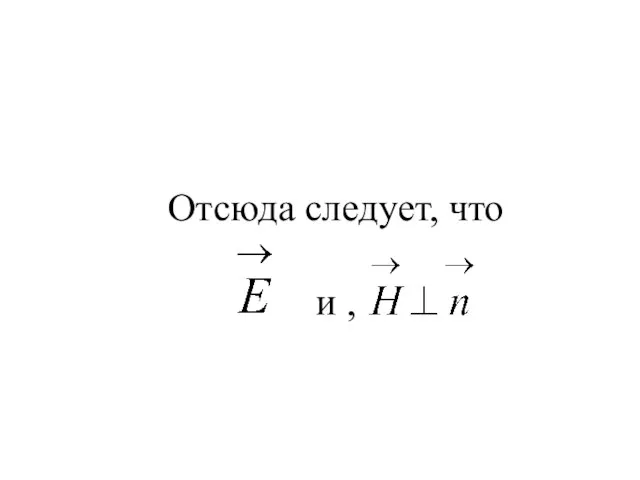









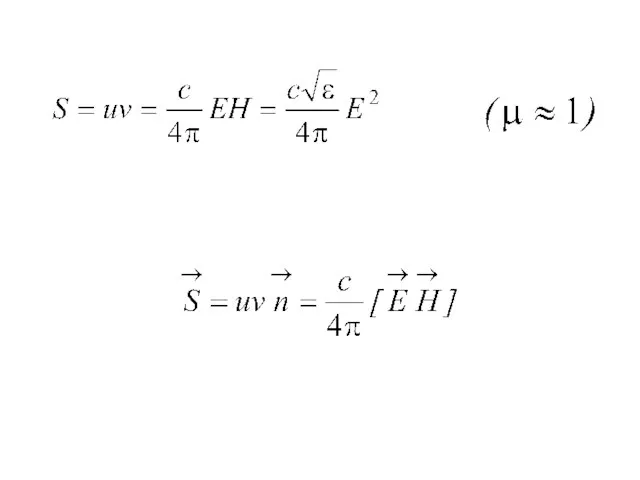



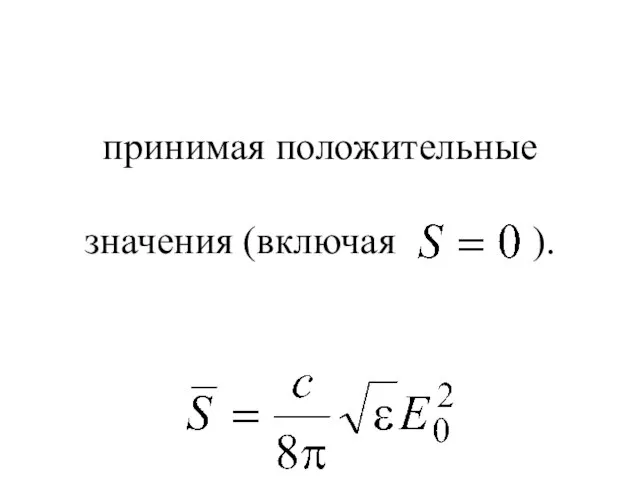




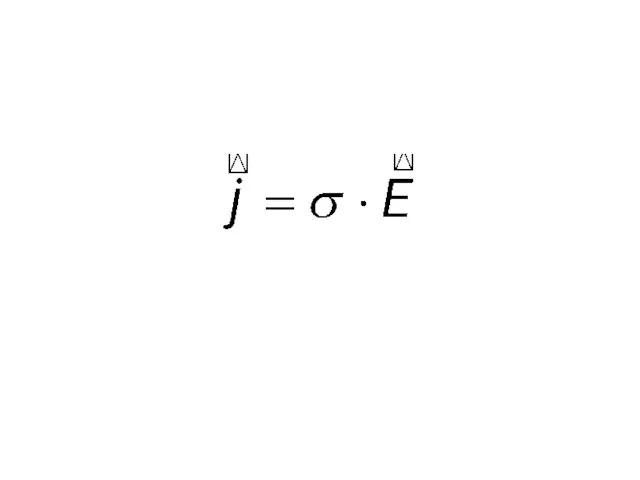






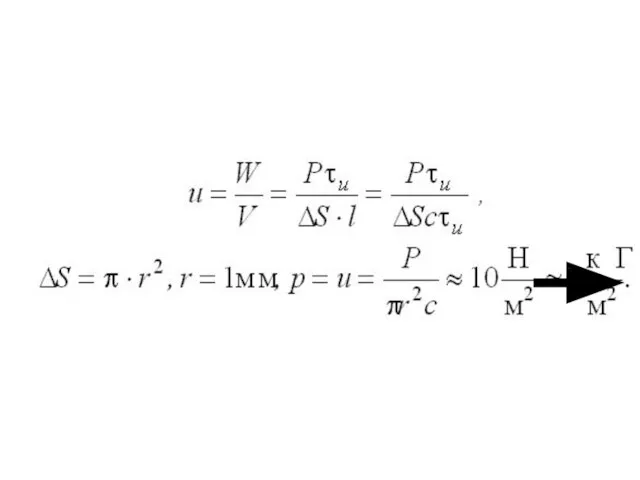
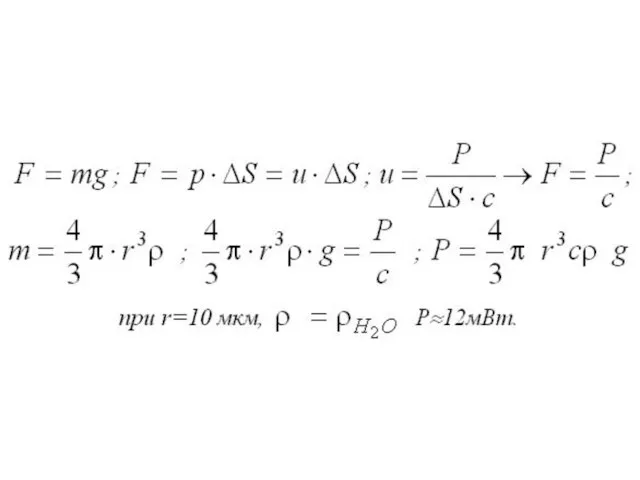
 «Время выбрало нас»
«Время выбрало нас» Производство корундовой броне-керамики в АО УАПО
Производство корундовой броне-керамики в АО УАПО «Senilia. Стихотворения в прозе» И. С. Тургенев
«Senilia. Стихотворения в прозе» И. С. Тургенев Русский язык
Русский язык Основные и дополнительные признаки государства
Основные и дополнительные признаки государства Подготовлено Sales House Media Plus Апрель, 2012
Подготовлено Sales House Media Plus Апрель, 2012 Листопадничек
Листопадничек Lebenslauf. Leben Lauf
Lebenslauf. Leben Lauf Отчет по 2 этапу проекта Государственное и муниципальное управление как отрасль профессиональной деятельности
Отчет по 2 этапу проекта Государственное и муниципальное управление как отрасль профессиональной деятельности Презентация на тему Измерение и построение углов
Презентация на тему Измерение и построение углов Проекции прямой
Проекции прямой Инициативный проект Велопешеходная дорожка с освещением в мкр. Юбилейный г.Губкин
Инициативный проект Велопешеходная дорожка с освещением в мкр. Юбилейный г.Губкин Лук и чеснокРецепты красоты и здоровья
Лук и чеснокРецепты красоты и здоровья Как понять другого человека через познание самого себя?
Как понять другого человека через познание самого себя? Татьянин день
Татьянин день Уголовное право США
Уголовное право США Урок по гимнастике в 7 классе
Урок по гимнастике в 7 классе Приглядывайтесь к облакам, Прислушивайтесь к птицам, Притрагивайтесь к родникам- Ничто не повторится. За мигом миг, за часом час В
Приглядывайтесь к облакам, Прислушивайтесь к птицам, Притрагивайтесь к родникам- Ничто не повторится. За мигом миг, за часом час В Путешествие по городу Таштаголу
Путешествие по городу Таштаголу История профсоюзного движения. Знаковые события
История профсоюзного движения. Знаковые события Устный опрос по теме «Логарифм»
Устный опрос по теме «Логарифм» Использование заданий в тестовой форме к тексту, разобранных на основе теории и технологии Способа диалектического обучения
Использование заданий в тестовой форме к тексту, разобранных на основе теории и технологии Способа диалектического обучения Основы развития корпоративной культуры в современных гостиницах
Основы развития корпоративной культуры в современных гостиницах Совместные программы, как инструмент интеграции российских вузов в европейское пространство высшего образования C.М. Яковлев, к
Совместные программы, как инструмент интеграции российских вузов в европейское пространство высшего образования C.М. Яковлев, к Промо-программа: При покупке ванны Cersanit cифон за 1 руб
Промо-программа: При покупке ванны Cersanit cифон за 1 руб Музыкальный шаблон для презентации
Музыкальный шаблон для презентации Николай Рубцов
Николай Рубцов АЛЮМИНИЙ
АЛЮМИНИЙ