Лекция 5. Транспортные задачии задачи о назначениях

Литература
Экономико-математические методы и прикладные модели: Учеб. пособие для вузов / Под ред. В.В. Федосеева. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. — раздел 3.2.
Фомин Г.П. Математические методы и модели в коммерческой деятельности: Учебник. – 2-е изд. М.: Финансы и статистика, 2005. — раздел 2.2.6.
Вентцель Е.С. Исследование операций: Задачи, принципы, методология. М.: Высшая школа, 2001.
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.1. Формулировка транспортной задачи
Дано:
Множество I, включающее m пунктов отправления груза, имеющегося в количествах ai (i=1…m)
Множество J, включающее n пунктов потребления, в каждом из которых имеется спрос на данный груз в количестве bj (j=1…n)
Затраты cij на перевозку единицы груза между пунктами i и j
Найти:
План перевозок X = (xij), согласно которому груз из пунктов отправления перевозится в пункты потребления с минимальными издержками, а спрос удовлетворяется полностью
Обычно предполагается, что общий размер запасов груза равен спросу (закрытая транспортная задача).
При этом условии задача всегда имеет оптимальное решение.
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.1.
Математическая запись
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.1
Получившаяся задача имеет форму задачи линейного программирования
Её можно решить симплексным методом
Однако есть более эффективные способы её решения
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

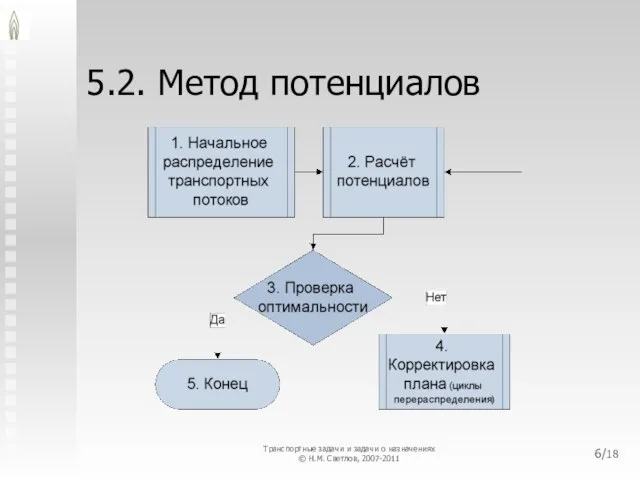
5.2. Метод потенциалов
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.2.1. Начальное распределение транспортных потоков
Теоретическая основа
Ранг матрицы ограничений транспортной задачи равен n+m–1 В оптимальном плане все переменные, кроме n+m–1, будут свободными
Следовательно, равными нулю
Метод северо-западного угла
Не использует данных о затратах
Обычно приводит к распределению, требующему много корректировок
Зато самый простой ☺
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

√
5.2.1
i=1, j=1
xij = min(a’i,b’j)
Если xij = a’i, то i ? i+1;
иначе j ? j+1
Если i>m, то процесс завершён;
иначе переход к 2.
√
Ещё не вывезенный остаток
Ещё не удовлетво-рённый спрос
√
√
20
Начальное распределение получено!
/18
i =1
j =1
i =2
i =3
j =2
j =3
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.2.2. Расчёт потенциалов
Теоретическая основа
Потенциалы приписываются поставщикам (ui) и потребителям (vj).
Уравнение потенциалов
cij = vj – ui
Расчёт потенциалов:
подобрать такие vj и ui, чтобы уравнение потенциалов выполнялось для всех базисных клеток (перевозок)
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.2.2
i = 1; ui = 0
В строке i находим множество столбцов J’ с ненулевыми перевозками и нерассчитанными потенциалами
Для всех j ∈ J’ выполняем
vj ? ui + cij
В столбце j находим множество строк I’ с ненулевыми перевозками и нерассчитанными потенциалами.
Для всех i ∈ I’ выполняем
ui ? vj – cij
Выполняем (2)
Процесс закончен, когда I’ или J’ оказывается пустым
Расчёт потенциалов завершён!
0
√
6
√
-2
√
6
√
0
√
12
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.2.3. Проверка оптимальности
Теоретическая основа
По используемым перевозкам cij разница в «ценах» (потенциалах) у потребителя j и у поставщика i равна стоимости перевозки
это следует из способа расчёта потенциалов
Неиспользуемая перевозка cij выгодна, если разница в «ценах» (потенциалах) у потребителя j и у поставщика i больше стоимости перевозки
Условие оптимальности
Разница в потенциалах потребителя и поставщика по всем неиспользуемым перевозкам не больше стоимости перевозки
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.2.3
Условие оптимальности
Разница в потенциалах потребителя и поставщика по всем неиспользуемым перевозкам не больше стоимости перевозки
В нашем примере выполняется не по всем неисп. перевозкам
Выполняется только для 1 ⮊ 2.
Значит, требуется переход к п.4. – корректировка плана
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011
-3
5
9
2

5.2.4. Корректировка плана
Выбираем клетку
с превышением разности потенциалов потребителя и поставщика над стоимостью транспортировки
как правило, с наибольшим
Строим контур (см. схему), начиная с данной клетки
Помечаем вершины контура знаками + и –
начинаем со знака + в выбранной свободной клетке
Находим наименьшую из величин в клетках со знаком –
Вычитаем её из всех клеток «–» и прибавляем ко всем клеткам «+»
Одну из клеток, в которых оказался нуль, объявляем свободной.
Переходим к проверке критерия оптимальности
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

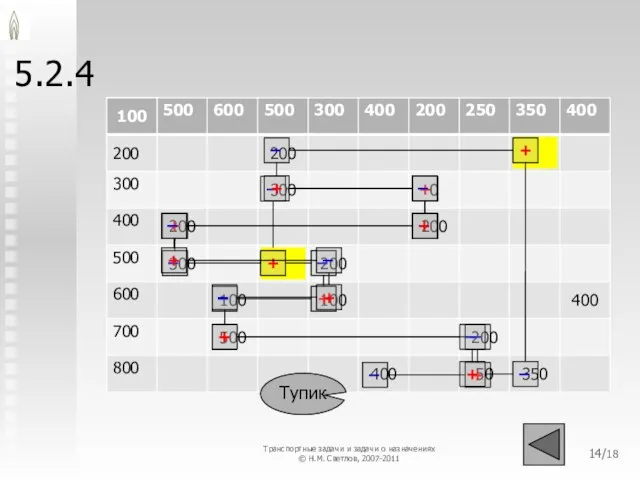
5.2.4
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.2.4
ОСОБЕННОСТИ
Контур можно построить всегда, но не всегда удаётся угадать правильный путь
В больших задачах отыскание циклов вручную может оказаться проблематичным
Для компьютерных программ это не составляет проблемы
Контур может оказаться вырожденным
Так случается, если наименьшим значением в клетке со знаком – оказывается нуль
Пересчёт по такому циклу не улучшает план, вследствие чего метод может зациклиться
в этом случае выбирают другую свободную клетку в качестве начальной
Если после пересчёта получились нули в нескольких клетках, в качестве свободной можно выбрать любую из них
Остальные считаются базисными с нулевым объёмом перевозки
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011

5.3. Особенности решения открытой транспортной задачи
/18
Транспортные задачи и задачи о назначениях © Н.М. Светлов, 2007-2011

5.4. Задача о назначениях
/18
Транспортные задачи и задачи о назначениях
© Н.М. Светлов, 2007-2011