Лекция 9

Мотивация
В действительности значения экономических переменных скорее подвержены частым колебаниям, нежели поступательному движению по направлению к стационарному состоянию или устойчивому росту.
Поэтому помимо теории роста нужна еще и теория, объясняющая эти колебания.
Традиционно колебания экономических переменных объяснялись изменениями совокупного спроса. Мы изучим эти модели в разделе, посвященном взаимодействию реального и денежного секторов.
Краткосрочные колебания и долгосрочная динамика объяснялись по-разному.
Однако, что если попытаться построить единую теорию роста и краткосрочных колебаний экономических переменных?

Тренд и колебания
Чтобы производить статистический анализ, желательно, чтобы рассматриваемые величины были стационарными. Выпуск, потребление, инвестиции, предложение труда – переменные, которые в моделях роста нестационарны. Они имеют тенденцию расти (а некоторые, например, продолжительность рабочей недели – возможно, падать) с течением времени. Иными словами эти величины имеют тренд.
Насколько постоянны ли темпы роста?
Насколько существенны колебания по сравнению с трендом?

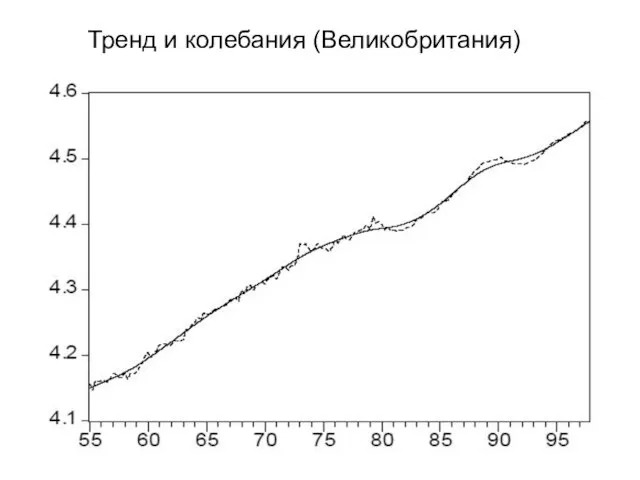
Тренд и колебания (Великобритания)

Освобождение от тренда
Раньше мы концентрировались на темпах прироста и абстрагировались от колебаний. Теперь сконцентрируемся на колебаниях. Для этого вычтем из рядов тренды. Такая процедура называется detrending, а алгоритм вычитания тренда называется фильтром. Фильтров существует множество. Нам нужно, чтобы фильтр дал стационарную переменную.

TS и DS ряды (1)
Многие нестационарные ряды бывают стационарными относительно детерминистского тренда (их называют TS – trend stationary) или относительно стохастического тренда, и тогда они оказываются стационарными в разностях, возможно, не первых (DS – difference stationary).
Соответственно, есть процедуры, нацеленные на различение TS и DS рядов. Например, работу по различению таких рядов для России проделали сотрудники ИЭПП и ВШЭ. Эконометрический анализ динамических рядов основных макроэкономических показателей, 2001.
http://www.iet.ru/publication.php?folder-id=44&category-id=116&publication-id=1721

TS и DS ряды (2)
Различие между TS и DS, грубо говоря, в следующем. Если ряд TS, то после особенно большого прироста переменной, может быть, не сразу, но будет ожидаться прирост меньший, чем в среднем. Если же ряд стационарен в первых разностях, то возникший прирост - это уже навсегда.
В ТШ (с. 311) на рис. 15.1 изображен выпуск, который является TS, а на рисунке 15.2 – DS.

Простейший фильтр
Самый простой фильтр таков: у нас есть динамический ряд. Логарифмируем его, строим линейную регрессию по времени и оставляем для анализа ошибки:
ln Yt = α + βt + yt.
Однако, здесь есть трудности.
Во-первых, темп роста может колебаться тоже колебаться (с какой-нибудь низкой частотой).
Во-вторых, нам ведь нужно, чтобы yt было стационарным. А для этого ряд в логарифмах должен быть TS.

Фильтр Ходрика-Прескотта (1)
Разработчики теории реальных деловых циклов (РДЦ) использовали Hodrick-Prescott, HP-filter. Рассмотрим его.
Выпуск разлагается на тренд и отклонения от него (в логарифмах):
yt = ygt + yct;
Теперь минимизируем сумму квадратов отклонений при ограничении, что сумма квадратов колебаний темпов прироста от периода к периоду не будет очень велика, т.е. тренд достаточно сглаженный. Сформулируем эту задачу так:

Фильтр Ходрика-Прескотта (2)
Однако в качестве параметра сглаживания возьмем не μ, а множитель Лагранжа:
Как изменяется вид тренда по мере роста параметра λ?

Фильтр Ходрика-Прескотта (3)
Чем выше λ, тем ближе тренд к линейному, который мы рассматривали выше.
При анализе квартальных данных стало традиционным использовать предложенное разработчиками значение λ = 1600.

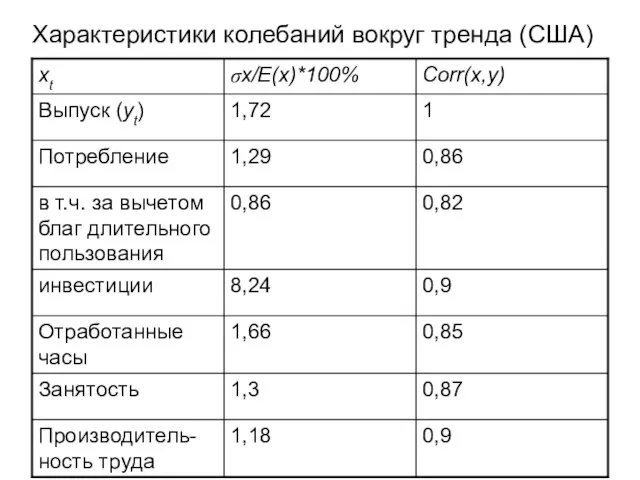
Характеристики колебаний вокруг тренда (США)

Характеристики колебаний вокруг тренда (США)
Потребление товаров текущего потребления и услуг колеблется в существенно меньшей степени, чем выпуск;
Инвестиции колеблются существенно больше.
Особенно велики колебания в запасах (17,3%).
Колебания общего числа отработанных часов (L) почти такие же, как у выпуска…
… и как у занятости.
Колебания средней продолжительности рабочей недели в часах существенно меньше, чем у выпуска.
Реальные зарплаты слабо коррелированы с выпуском, но:
По данным национальных счетов корреляция отсутствует, тогда как
По данным опросов корреляция положительная.
Производительность труда положительно коррелирует с выпуском.

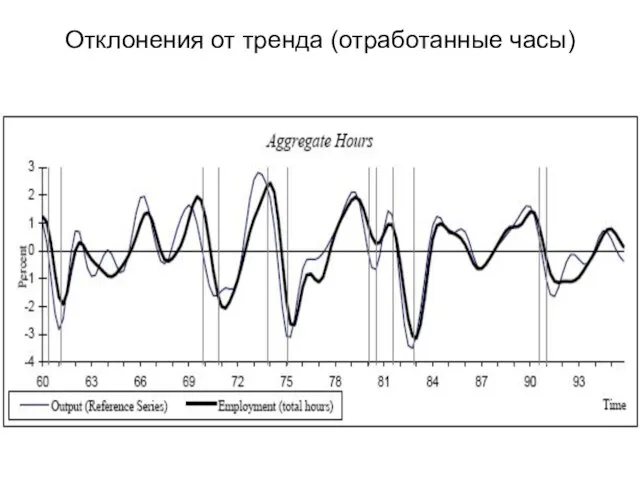
Отклонения от тренда (отработанные часы)

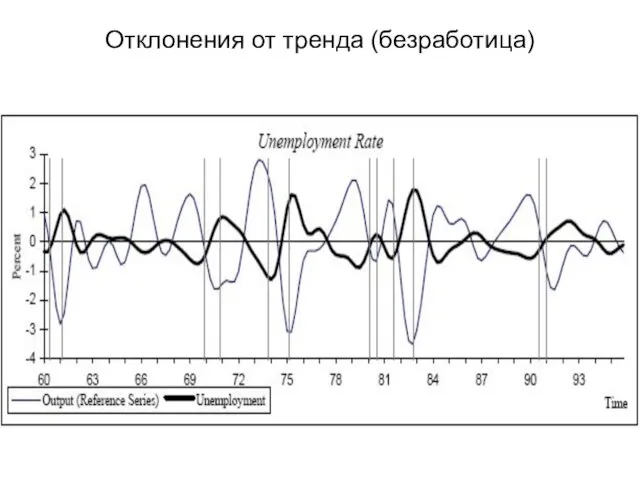
Отклонения от тренда (безработица)

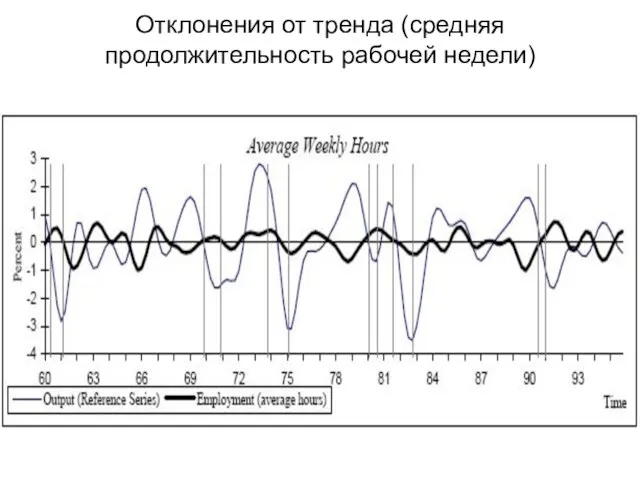
Отклонения от тренда (средняя продолжительность рабочей недели)

Предпосылки модели (1)
В качестве базовой модели будем использовать модель Рамсея.
Время дискретное.

Предпосылки модели (2) – рынки факторов

Предпосылки модели (3) – потребление

Предпосылки модели (4) - бюджетное ограничение

Предпосылки модели (5) – накопление капитала
Все активы семьи являются капиталом. Однако, как и ранее, для нас важна капиталовооруженность эффективной (а не настоящей) единицы труда. Тогда динамика накопления капитала будет выглядеть следующим образом:

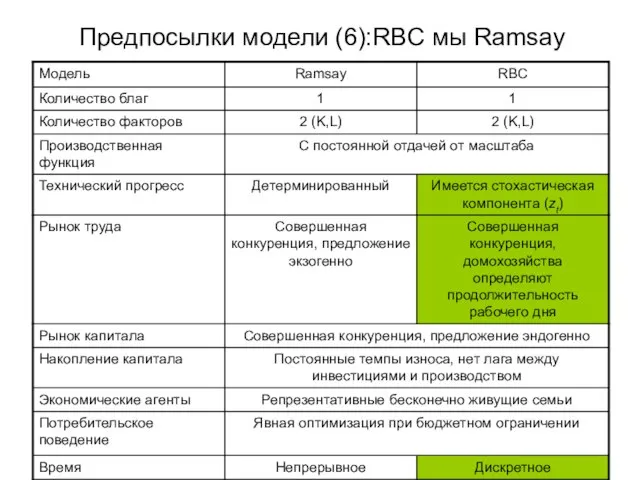
Предпосылки модели (6):RBC мы Ramsay

Решение модели (попытка, 1)

Решение модели (попытка, 2)

Решение модели (попытка, 3)

Решение модели (попытка, 4)

Увы, построенная модель не имеет аналитического решения. Можно либо упростить ее, либо решить численными методами.
Чтобы не потерять полезные свойства, пойдем вторым путем. При этом используем метод калибровки (который очень полюбился работающим с РДЦ)

Идея калибровки
В модели РДЦ используются параметры, например, темпы роста населения, темпы технического прогресса, параметры технологических шоков, коэффициенты дисконтирования и износа капитала. Можно воспользоваться проведенными заранее измерениями таких параметров, вставить их в модель и понаблюдать за динамикой экономики с такими параметрами.
Далее рассмотрим калибровку для экономики США, проведенную Кули и Прескоттом:
Cooley T.F., Prescott E. Economic Growth and Business Cycles / In Frontiers of Business Cycles Research (ed. Cooley T.F.), Princeton University Press, Princeton, 1995., pp. 1-37.

Калибровка (1)
α: поскольку в модели используется производственная функция Кобба-Дугласа с суммой коэффициентов равной единице, это доля дохода на капитал в факторных доходах.
Примем для США: α = 0,4.
Это выше, чем стандартные цифры (обычно 1/3 или 0,36), потому что Кули и Прескотт включают в капитал также потребительские блага длительного пользования и государственные инвестиции.
Для России, α, вероятно, еще выше.

Калибровка (2)
g – средние темпы роста производительности труда. Для США этот показатель равен 1,56% в год.
Поскольку обычно в модели используются квартальные данные, g = (1,0156)1/4-1=0,0039.
Для России этот показатель составил за период 2001-2004 год 0,0147 в квартал, но неясно, насколько эта цифра устойчива.
ρ – показатель автокоррелированности шоков производительности. Оценка для США (при квартальных данных) 0,95 с достаточно большим разбросом;
ε – среднеквадратичное отклонение неавтокоррелированной компоненты шока: 0,007.
n – темпы роста населения. Для США – 1,2% в год, то есть n = 0,003.

Калибровка (3)

Калибровка (4)