лекция 4

Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).

Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию (которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).

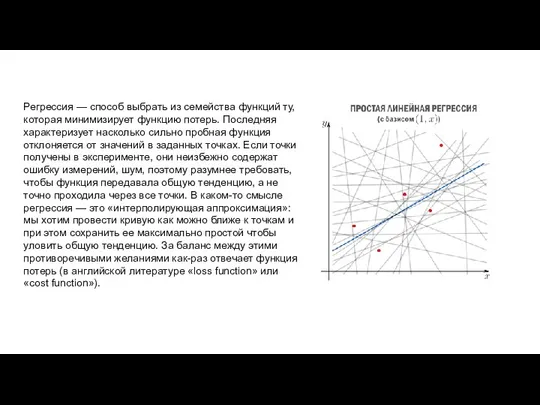
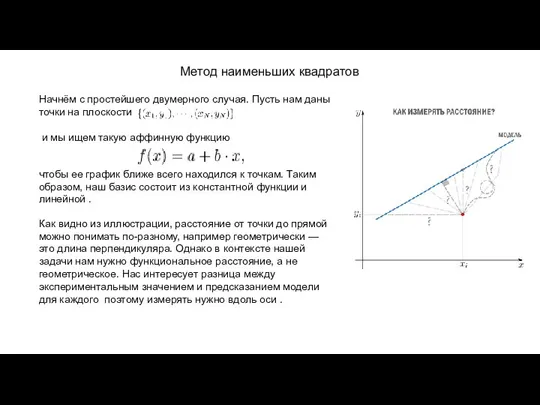
Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости и мы ищем такую аффинную функцию
чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной .
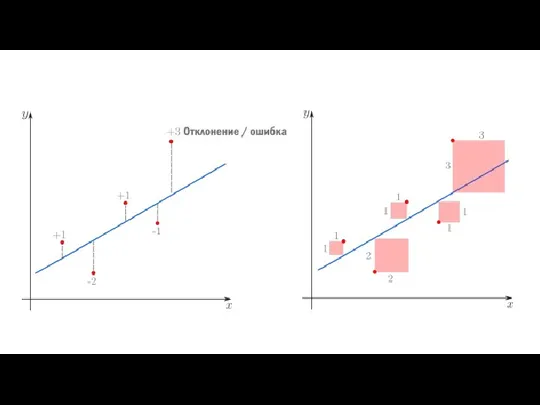
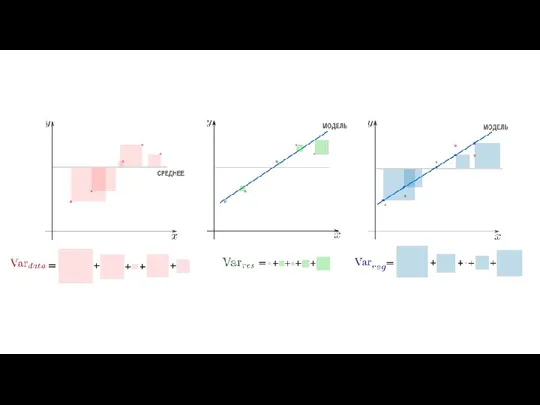
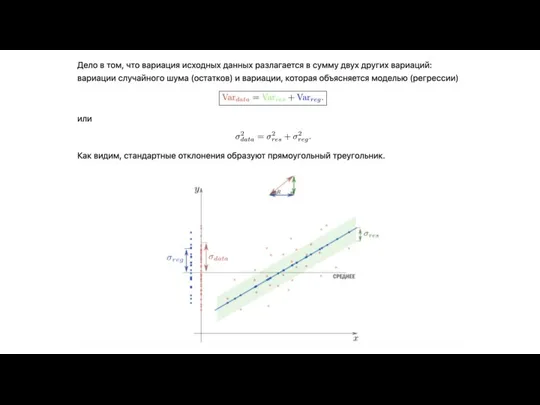
Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого поэтому измерять нужно вдоль оси .
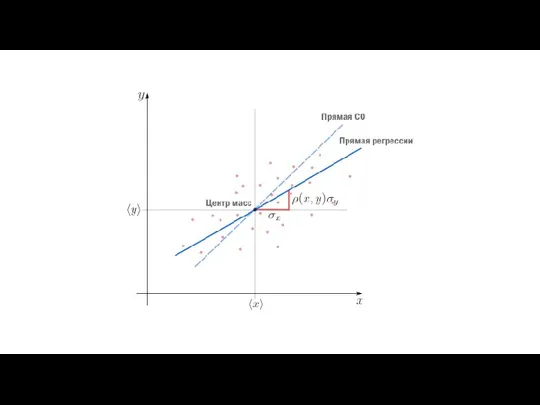
Метод наименьших квадратов

Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц . Простейший вариант — сумма модулей отклонений приводит к Least Absolute Distance (LAD) регрессии.
Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)
Метод наименьших квадратов (по англ. OLS) — линейная регрессия c в качестве функции потерь.

Наша задача — найти параметры ?̂ и ?̂, минимизирующие SSE(?,?) . Эту функцию иногда называют функцией ошибок, функцией соответствия или функцией потерь.
(?̂,?̂ )=argmin?,?SSE(?,?).
Простейший способ найти — вычислить частные производные по и , приравнять их нулю и решить систему линейных уравнений
Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям

Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения отклоняется от своего среднего значения меньше чем , потому что: