Содержание
- 2. Алгоритм определения ПМВНР
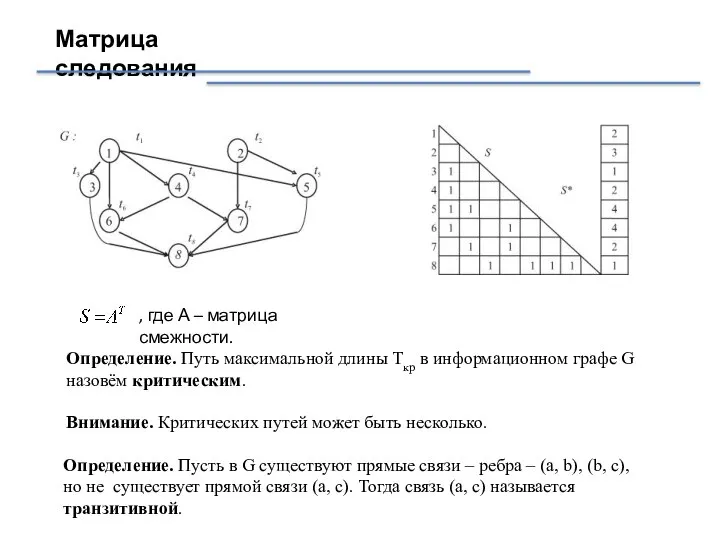
- 3. Матрица следования , где А – матрица смежности. Определение. Путь максимальной длины Tкр в информационном графе
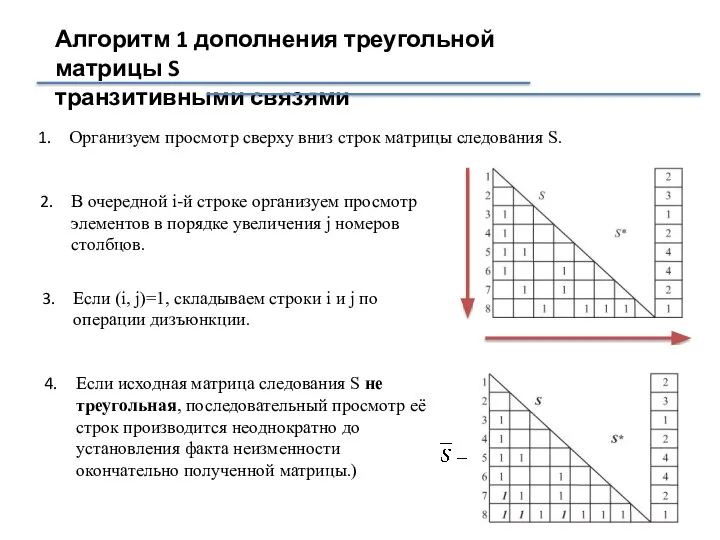
- 4. Алгоритм 1 дополнения треугольной матрицы S транзитивными связями Организуем просмотр сверху вниз строк матрицы следования S.
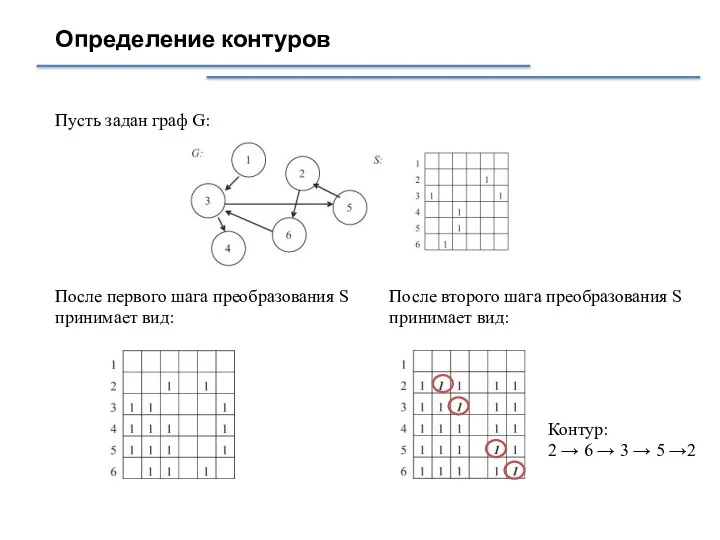
- 5. Определение контуров Пусть задан граф G: После первого шага преобразования S принимает вид: После второго шага
- 6. Полное множество взаимно независимых работ (ПМВНР) Определение. Работы a и b будем называть взаимно независимыми, если
- 7. Полное множество взаимно независимых работ (ПМВНР) Столбец 1. ПМВНР = {1, 2} Столбец 2. ПМВНР =
- 8. Алгоритмы определения ранних и поздних сроков выполнения операций
- 9. Ранние и поздние сроки выполнения работ Ранний срок τ1i окончания выполнения работы – минимальный срок окончания
- 10. Алгоритм нахождения ранних сроков окончания выполнения работ Полагаем первоначально τ11 = τ12 = ... = τ1m
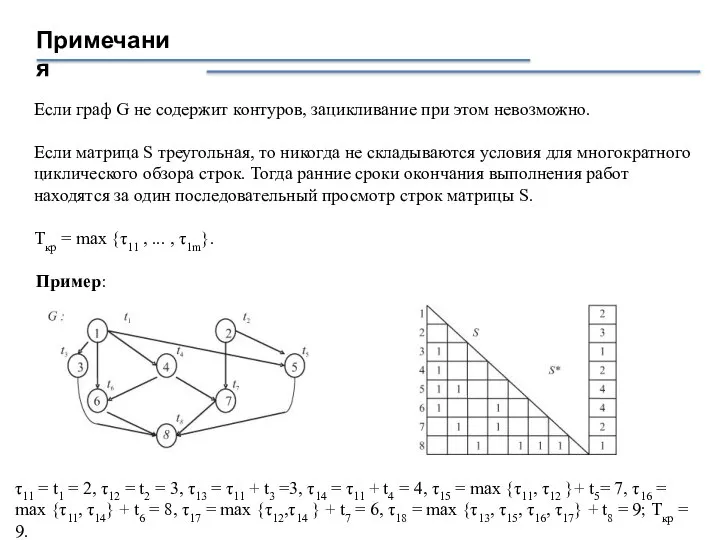
- 11. Примечания Если граф G не содержит контуров, зацикливание при этом невозможно. Если матрица S треугольная, то
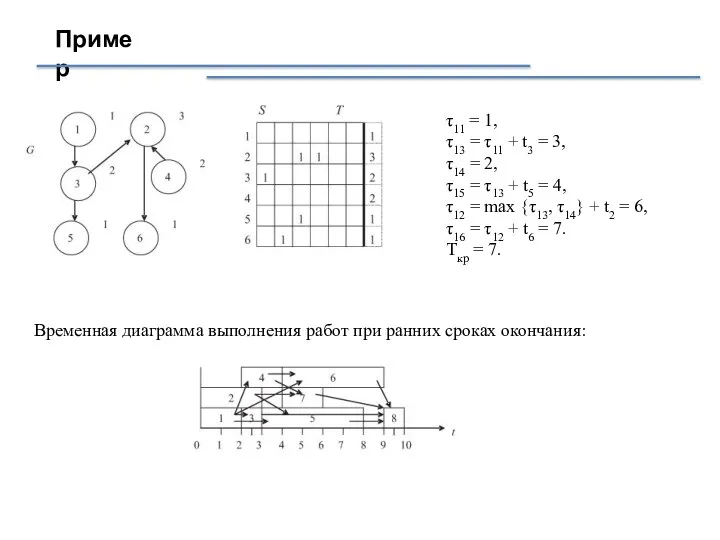
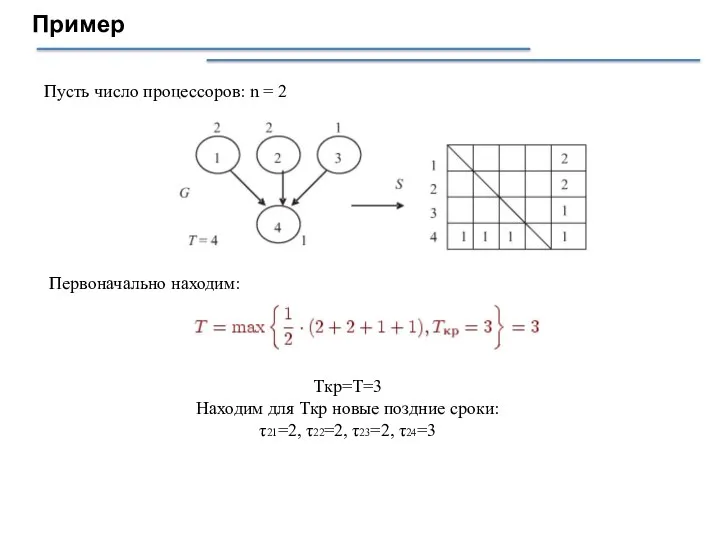
- 12. Пример τ11 = 1, τ13 = τ11 + t3 = 3, τ14 = 2, τ15 =
- 13. Алгоритм нахождения поздних сроков окончания выполнения работ при заданном значении Т Полагаем первоначально τ21(T) = ...
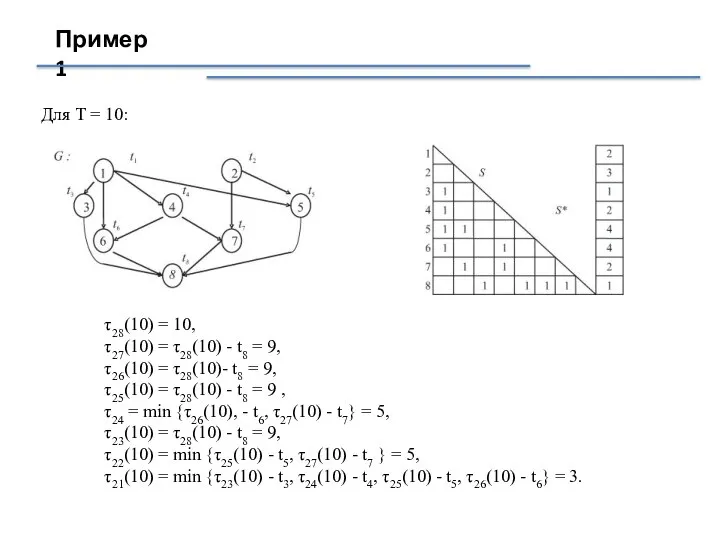
- 14. Пример 1 Для T = 10: τ28(10) = 10, τ27(10) = τ28(10) - t8 = 9,
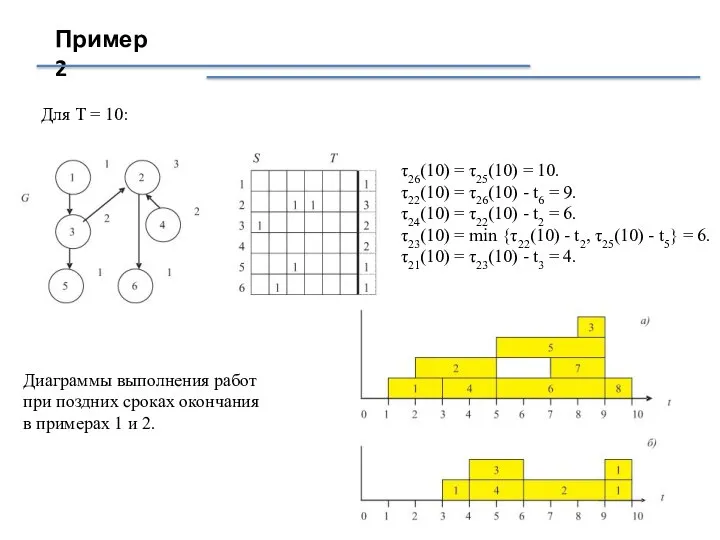
- 15. Пример 2 Для T = 10: τ26(10) = τ25(10) = 10. τ22(10) = τ26(10) - t6
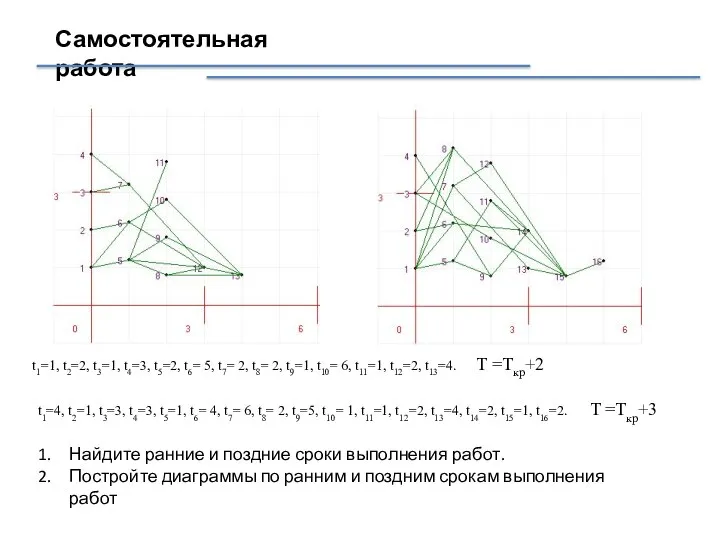
- 16. Самостоятельная работа Найдите ранние и поздние сроки выполнения работ. Постройте диаграммы по ранним и поздним срокам
- 17. Алгоритмы поиска наименьших ресурсов: процессов и времени
- 18. Плотность загрузки вычислительной системы Определение. Функция где: называется плотностью загрузки, найденной для значений τ1, …, τm
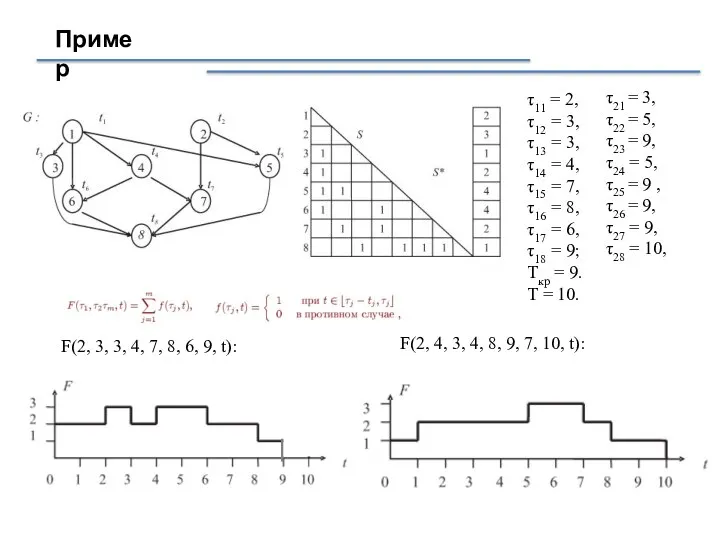
- 19. Пример τ11 = 2, τ12 = 3, τ13 = 3, τ14 = 4, τ15 = 7,
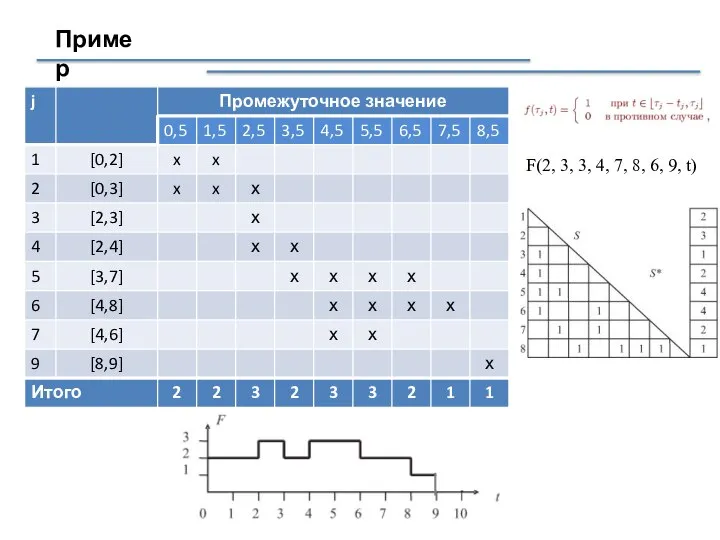
- 20. Пример F(2, 3, 3, 4, 7, 8, 6, 9, t)
- 21. Максимальная ширина графа Дано: граф G, L – число ПМВНР, ri – число работ, образующих i-е
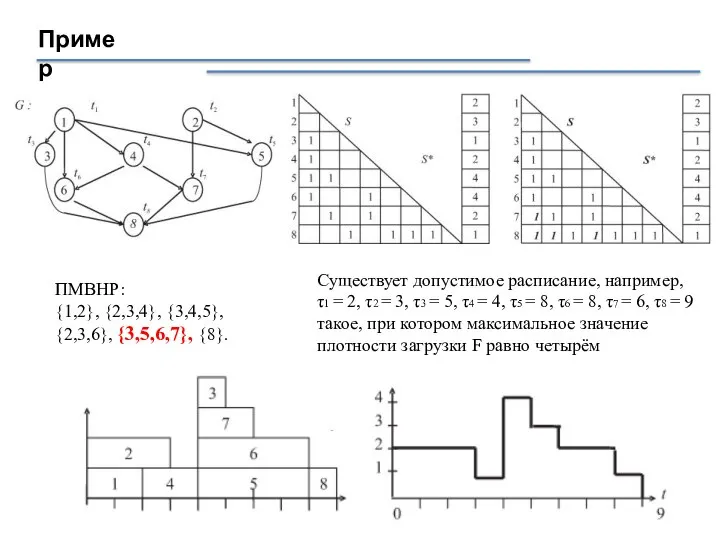
- 22. Пример ПМВНР: {1,2}, {2,3,4}, {3,4,5}, {2,3,6}, {3,5,6,7}, {8}. Существует допустимое расписание, например, τ1 = 2, τ2
- 23. Загрузка отрезка для допустимого расписания Определение. Функция называется загрузкой отрезка [θ1, θ2] ⊂ [0,T] для заданного
- 24. Пример Для отрезка времени [0, 4] ⊂ [0, 10]: Ф = 9 Для отрезка времени [1,
- 25. Минимальные оценки работ и вычислительных ресурсов Определение. Функция называется минимальной загрузкой отрезка [θ1, θ2] ⊂ [0,
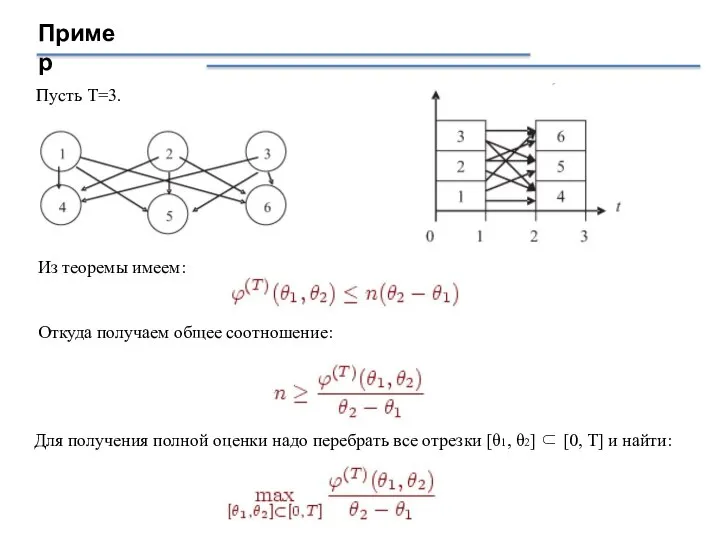
- 26. Пример Пусть T=3. Из теоремы имеем: Откуда получаем общее соотношение: Для получения полной оценки надо перебрать
- 27. Продолжение примера Проанализируем все возможные отрезки [θ1, θ2] ⊂ [0, 3] : ϕ(3)(0, 1) = ϕ(3)
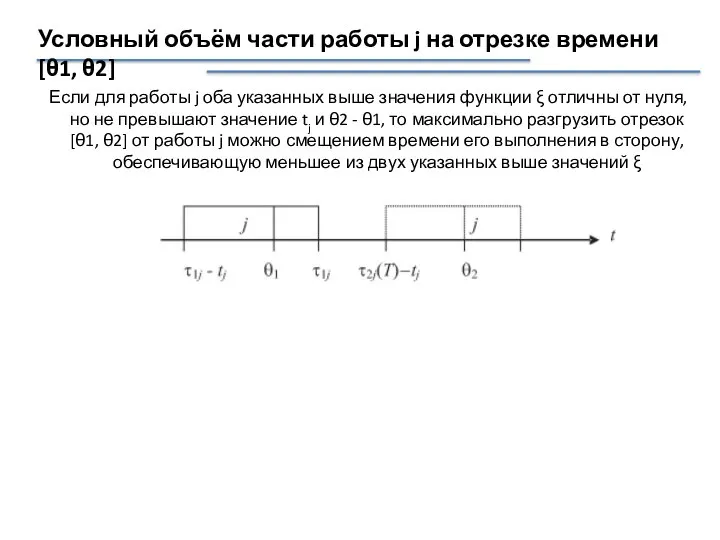
- 28. Условный объём части работы j на отрезке времени [θ1, θ2] Определим функцию: 1) Значение ξ(τ1j -
- 29. Если для работы j оба указанных выше значения функции ξ отличны от нуля, но не превышают
- 30. б) τ1j ≥ θ2 Λ τ2j(T) - tj ≤ θ1, в этом случае очевидно, что tj
- 31. Алгоритм нахождения значения функции ϕ(T)(θ1, θ2). Предполагаем, что для каждой работы j = 1, ... ,
- 32. Алгоритм нахождения значения функции ϕ(T)(θ1, θ2). Теорема 2. Пусть заданный алгоритм выполняется на ВС, состоящей из
- 33. Нижняя оценка минимального числа процессоров, необходимого для выполнения алгоритма за заданное время 1. Первоначально полагаем n
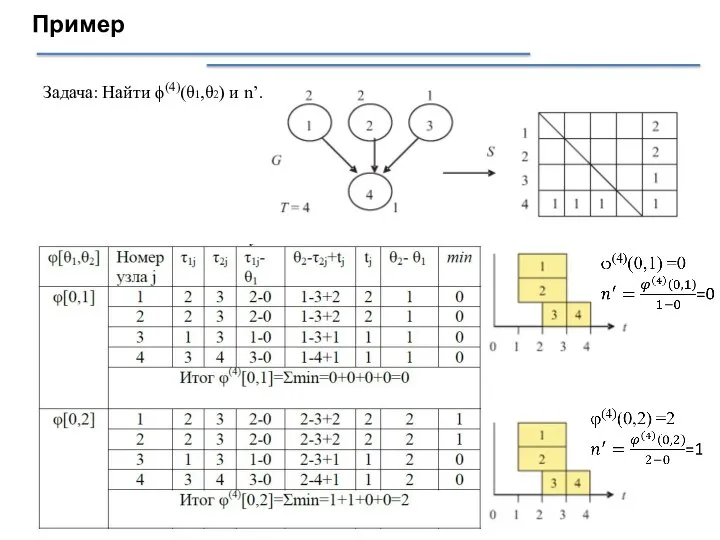
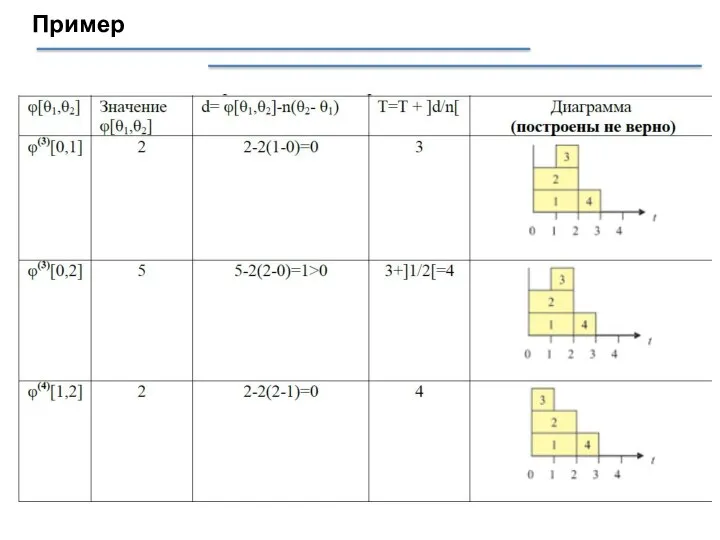
- 34. Пример Задача: Найти ϕ(4)(θ1,θ2) и n’.
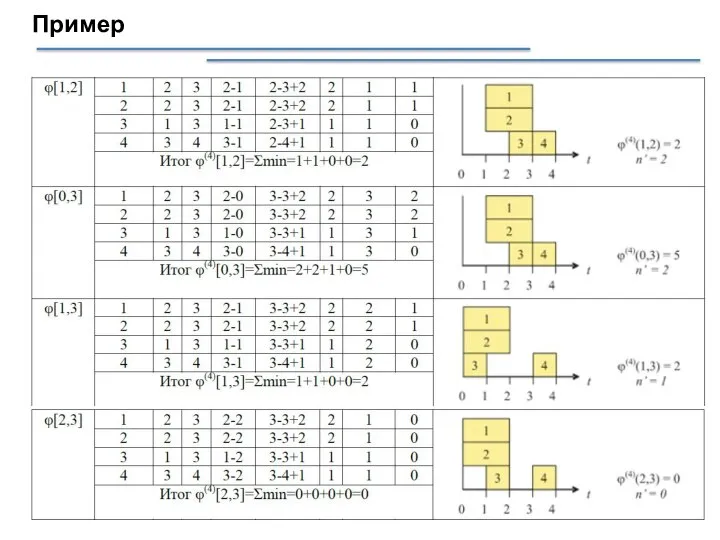
- 35. Пример
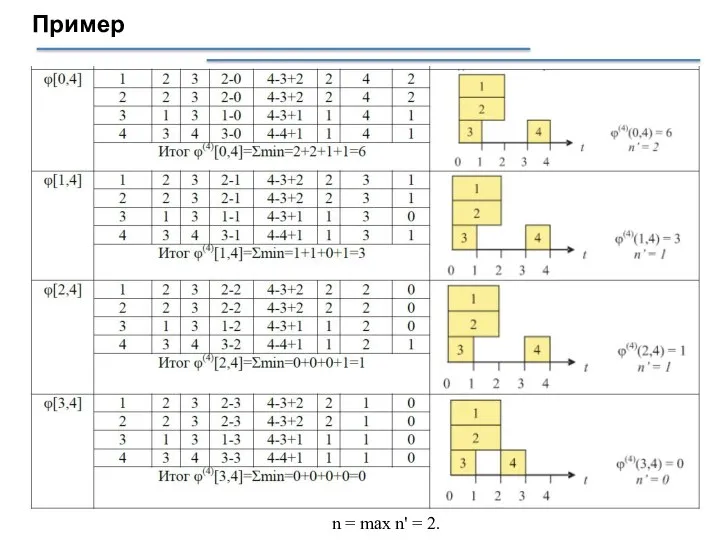
- 36. Пример n = max n' = 2.
- 37. Нижняя оценка минимального времени выполнения данного алгоритма на ВС 1. Первоначально полагаем: 2. Организуем перебор всех
- 38. Пусть число процессоров: n = 2 Пример Первоначально находим: Tкр=T=3 Находим для Ткр новые поздние сроки:
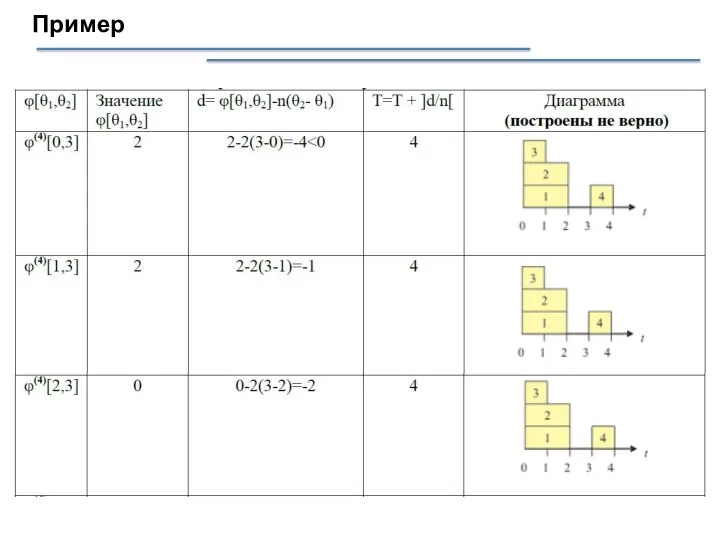
- 39. Пример
- 40. Пример
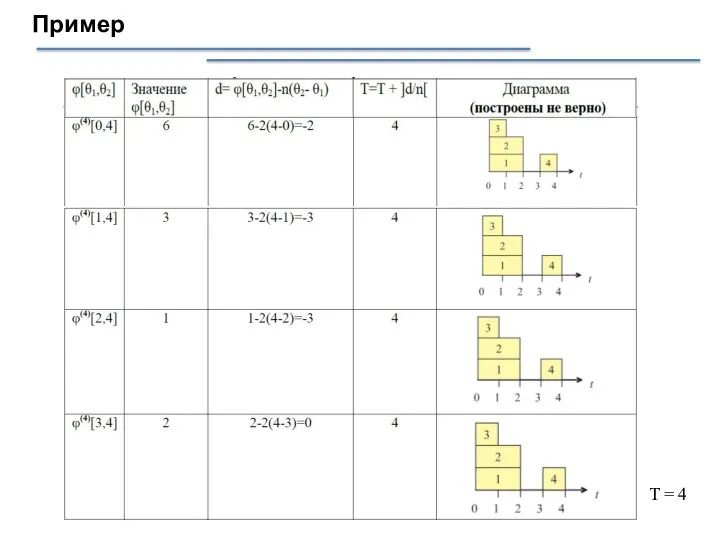
- 41. Пример T = 4
- 43. Скачать презентацию










![Загрузка отрезка для допустимого расписания Определение. Функция называется загрузкой отрезка [θ1, θ2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/983024/slide-22.jpg)
![Пример Для отрезка времени [0, 4] ⊂ [0, 10]: Ф = 9](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/983024/slide-23.jpg)

![Продолжение примера Проанализируем все возможные отрезки [θ1, θ2] ⊂ [0, 3] :](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/983024/slide-26.jpg)
![Условный объём части работы j на отрезке времени [θ1, θ2] Определим функцию:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/983024/slide-27.jpg)





 Устный счёт Состав числа 6 (1 класс)
Устный счёт Состав числа 6 (1 класс) Астана, Ноябрь 2011
Астана, Ноябрь 2011 Патриотическое воспитание
Патриотическое воспитание Консоли PS4 Slim (Pro) и Xbox One S
Консоли PS4 Slim (Pro) и Xbox One S Тема: «Общая характеристика плоских, круглых и кольчатых червей. Роль червей в природе, жизни человека».
Тема: «Общая характеристика плоских, круглых и кольчатых червей. Роль червей в природе, жизни человека». Химическая связь
Химическая связь  Художники рисуют космос
Художники рисуют космос Организация книжных выставок - это наука или искусство!?
Организация книжных выставок - это наука или искусство!? Психологическое оружие
Психологическое оружие Гражданин и государство
Гражданин и государство Использование ИКТ для развития творческих способностей детей на уроках физической культуры
Использование ИКТ для развития творческих способностей детей на уроках физической культуры Ланец Екатерина Артуровна Учитель начальных классов . Стаж работы в школе-32 года Закончила Серовское педагогическое училище в 197
Ланец Екатерина Артуровна Учитель начальных классов . Стаж работы в школе-32 года Закончила Серовское педагогическое училище в 197 Nature’s Sunshine 2019
Nature’s Sunshine 2019 С праздником 8 марта
С праздником 8 марта 11-12 мая 2012 года в Алматинском Технологическом Университете состоялась Республиканская предметная олимпиада среди студентов высш
11-12 мая 2012 года в Алматинском Технологическом Университете состоялась Республиканская предметная олимпиада среди студентов высш 2 день семинара
2 день семинара Все, что нужно знать про рекламу в Facebook
Все, что нужно знать про рекламу в Facebook РУССКИЙ ЯЗЫК И ОБЩЕСТВО
РУССКИЙ ЯЗЫК И ОБЩЕСТВО Фёдорова Светлана Александровна, учитель русского языка и литературы МОУОО школы №4
Фёдорова Светлана Александровна, учитель русского языка и литературы МОУОО школы №4 Система финансового администрирования и контроля для территориально распределенных холдинговых структур
Система финансового администрирования и контроля для территориально распределенных холдинговых структур | Ключ к неорганическим материалам
| Ключ к неорганическим материалам Презентация на тему Текстильная промышленность
Презентация на тему Текстильная промышленность  Развитие жизни в мезозойскую эру
Развитие жизни в мезозойскую эру Forte 2 unita 5
Forte 2 unita 5 Отравление ядохимикатами Выполнил студент группы М-422 Посохов Олег
Отравление ядохимикатами Выполнил студент группы М-422 Посохов Олег Основные угрозы национальным интересам
Основные угрозы национальным интересам ДЗ
ДЗ 129626, г.Москва, Графский переулок д.9, стр.2. тел.:(495)9335900, 3635612(13). Факс:9335901. e-mail:
129626, г.Москва, Графский переулок д.9, стр.2. тел.:(495)9335900, 3635612(13). Факс:9335901. e-mail: