Содержание
- 2. Лекция № 9 Статистический анализ случайных погрешностей
- 3. Статистический анализ случайных погрешностей Причины разброса времени скатывания: неровности доски, обусловленное этими неровностями различие траекторий при
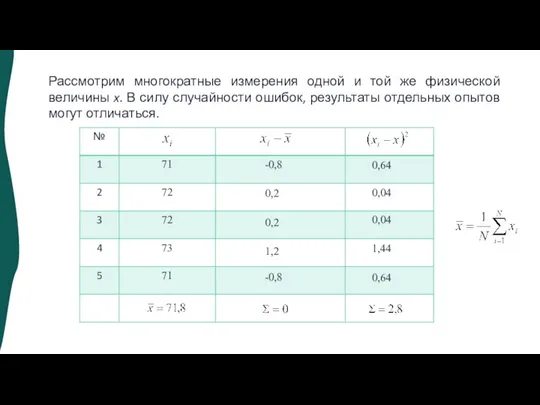
- 4. Рассмотрим многократные измерения одной и той же физической величины x. В силу случайности ошибок, результаты отдельных
- 5. Рассмотрим многократные измерения одной и той же физической величины x. В силу случайности ошибок, результаты отдельных
- 6. Рассмотрим многократные измерения одной и той же физической величины x. В силу случайности ошибок, результаты отдельных
- 7. Стандартным отклонением результатов измерений называется величина, определяемая выражением: Квадрат стандартного отклонения называют дисперсией: В случае, когда
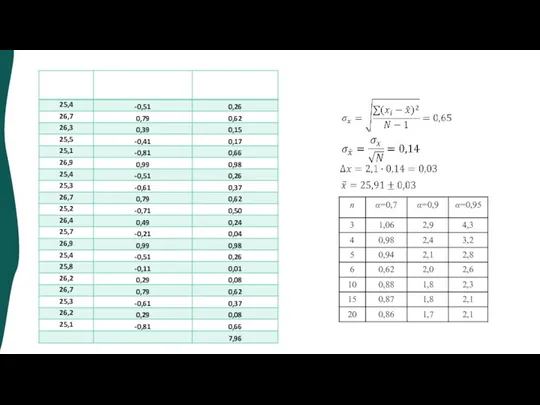
- 8. Пример: В случае, если измерений много, то Стандартное отклонение показывает погрешность единичного измерения. Для того, чтобы
- 9. Пример:
- 12. Что показывает стандартное отклонение Среднее значение Стандартное отклонение Расчеты с помощью Excel
- 14. Скачать презентацию









 Личность тренера в командообразовании
Личность тренера в командообразовании Барельеф натюрморта из двух предметов со складками драпировки. 3 класс
Барельеф натюрморта из двух предметов со складками драпировки. 3 класс Рынок автокредитования
Рынок автокредитования Сочинение по картине О. Кипренского "Портрет Натальи Викторовны Кочубей"
Сочинение по картине О. Кипренского "Портрет Натальи Викторовны Кочубей" Проект по снижению дорожной аварийности в Мурманской области
Проект по снижению дорожной аварийности в Мурманской области Paperchilli. Фирменный стиль
Paperchilli. Фирменный стиль Приобретаемая база в январе 2018 года под дилерский центр в городе Ульяновск
Приобретаемая база в январе 2018 года под дилерский центр в городе Ульяновск OKiR_Lektsia_5
OKiR_Lektsia_5 Использование информационно - коммуникативных технологий на уроках в начальной школе Захарова Наталья Владимировна учитель нача
Использование информационно - коммуникативных технологий на уроках в начальной школе Захарова Наталья Владимировна учитель нача Техническая поддержка: от услуги к партнерству (размышления на вольную тему)
Техническая поддержка: от услуги к партнерству (размышления на вольную тему) Комплексная программа«Сетевой город»
Комплексная программа«Сетевой город» Кришна (Верховная Личность Бога)
Кришна (Верховная Личность Бога) Шамшырақ жасау біз үшін
Шамшырақ жасау біз үшін Презентация без названия (1)
Презентация без названия (1) Презентация на тему Изобразительное искусство классицизма и рококо
Презентация на тему Изобразительное искусство классицизма и рококо  Цифры
Цифры Стратегия публичного выступления. Занятие №42
Стратегия публичного выступления. Занятие №42 Культура Японии 9 класс
Культура Японии 9 класс И это всё о ней…
И это всё о ней… Обучение детей дошкольного возраста правилам безопасного поведения на дорогах
Обучение детей дошкольного возраста правилам безопасного поведения на дорогах Презентация на тему У истоков цивилизации
Презентация на тему У истоков цивилизации  Тема урока: Сила трения.. Цель урока: Выяснить: а) причины возникновения силы трения; силы трения; б) возможности ее б) возможности ее
Тема урока: Сила трения.. Цель урока: Выяснить: а) причины возникновения силы трения; силы трения; б) возможности ее б) возможности ее  Профилактика и лечение гриппа, ОРВИ и заболеваний носоглотки в рамках комплексной программы "Здоровье населения".
Профилактика и лечение гриппа, ОРВИ и заболеваний носоглотки в рамках комплексной программы "Здоровье населения". 3 причины освоить скорочтение
3 причины освоить скорочтение Основные функциональные возможности программы
Основные функциональные возможности программы Проектирование участка механического цеха обработки детали Вал
Проектирование участка механического цеха обработки детали Вал Требования к средствам учета электрической энергии
Требования к средствам учета электрической энергии «Свежий ветер» (команда ГОУСОШ № 108)
«Свежий ветер» (команда ГОУСОШ № 108)