Содержание
- 2. Тема 7
- 3. Тема 7 7.6.Теоретические основы вибрационного перемещения Вибрационное перемещение – среднее одностороннее направленное движение тел под действием
- 4. Тема 7 В последнем выражении N – сила нормального давления, которая определится из уравнения проекций всех
- 5. Тема 7 – граничное состояние между проскальзыванием и покоем; – тело будет двигаться вместе с плоскостью;
- 6. Тема 7 7.7. Механический КПД механизмов и машин Коэффициент полезного действия (КПД) − это безразмерная величина,
- 7. Тема 7 Тогда где коэффициент потерь, который показывает, какая часть работы движущих сил расходуется на преодоление
- 8. Тема 7 Последовательное соединение механизмов Рассмотрим машину, состоящую из последовательно соединенных механизмов, условно обозначенных на схеме
- 9. Тема 7 Найдем произведение частных КПД (2) Сравнивая (1) и (2), можно сделать вывод, что они
- 10. Тема 7 Общий КПД машины (3) Так как Подставив эти выражения в (3), получим Отсюда следует,
- 11. Тема 7 Сравним варианты последовательного и параллельного соединения механизмов с точки зрения минимизации механических потерь в
- 12. Тема 8 Тема 8. Введение в динамику машин 8.1. Основные задачи и методы динамики машин Динамика
- 13. Тема 8 Объектом изучения в динамике машин является машинный агрегат. В общем виде его можно представить
- 14. Тема 8 Работа – это физическая величина, характеризующая преобразование энергии из одной формы в другую. Элементарная
- 15. Тема 8 Кинетическая энергия – это накопленная работа, совершаемая над механической системой с целью сообщения этой
- 16. Тема 8 8.2. Выбор динамической модели машинного агрегата Машинные агрегаты являются сложными многозвенными и многосвязными электромеханическими,
- 17. Тема 8 Во всех случаях следует стремиться к использованию наиболее простых динамических моделей, адекватных исследуемым процессам.
- 18. Тема 8 В качестве звена приведения целесообразно выбрать такое, которое не изменяет направление движения в пределах
- 19. Тема 8 8.3. Приведение сил и моментов сил Определим значения приведенных сил и моментов сил, принимая
- 20. Тема 8 Пусть звено приведения совершает поступательное движение. Тогда Nп=Fп•VA , где Fп – приведенная сила;
- 21. Тема 8
- 22. Тема 8 8.4. Приведение масс и моментов инерции Для нахождения приведенных масс и моментов инерции воспользуемся
- 23. Тема 8
- 24. Тема 8
- 25. Тема 8
- 26. Тема 8
- 27. Тема 8 8.5. Режимы движения машинных агрегатов и их энергетические характеристики Полным временем движения машинного агрегата
- 28. Тема 8 2. Период установившегося движения (Ту) – период движения, при котором угловая скорость ведущего звена
- 29. Тема 8 3. Период выбега или остановки (Тв) – период времени, в течение которого происходит снижение
- 30. Тема 8 Исследование переходных режимов необходимо для нахождения времени срабатывания машинного агрегата, которое определяет быстродействие многих
- 31. Тема 8 В режиме установившегося движения работает большинство технологических и энергетических машин: металлорежущие станки, кривошипные прессы,
- 33. Скачать презентацию
Слайд 3Тема 7
7.6.Теоретические основы вибрационного перемещения
Вибрационное перемещение – среднее одностороннее направленное движение
Тема 7
7.6.Теоретические основы вибрационного перемещения
Вибрационное перемещение – среднее одностороннее направленное движение

(1)
где s – перемещение; δ – размах колебаний;
– частота колебаний.
Сила инерции Ф определится выражением
Ф = – m . а, (2)
где m – масса тела; а – ускорение движения.
Дифференцируя дважды (1) и подставляя ускорение в (2), получим
(3)
Силу трения Fтр. найдем, используя закон Кулона:
Fтр. = fтр. .N.
Слайд 4Тема 7
В последнем выражении N – сила нормального давления, которая определится
Тема 7
В последнем выражении N – сила нормального давления, которая определится

(4)
(5)
где g – ускорение свободного падения;
fтр. – коэффициент трения скольжения;
α – угол бросания.
Сила трения в выражениях (4) и (5) будет переменной по величине и направлению
(6)
Эта сила будет являться движущей силой, вызывающей вибрационное перемещение, т.е. проскальзывание тела по шероховатой поверхности либо вперед, либо назад в зависимости от соотношения между силами тяжести и инерции.
Введем горизонтальную амплитуду колебаний Тогда из выражения (4), с учетом (6), получим следующие возможные варианты относительного движения:
Слайд 5Тема 7
– граничное состояние между проскальзыванием и покоем;
– тело будет
Тема 7
– граничное состояние между проскальзыванием и покоем;
– тело будет
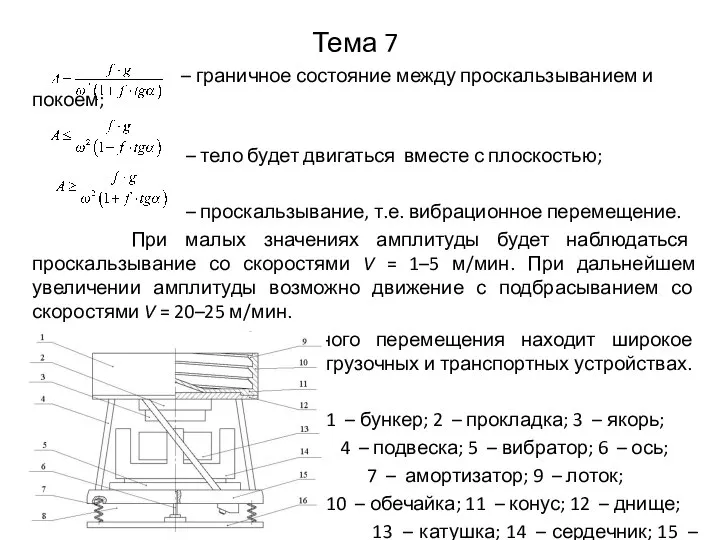
– проскальзывание, т.е. вибрационное перемещение.
При малых значениях амплитуды будет наблюдаться проскальзывание со скоростями V = 1–5 м/мин. При дальнейшем увеличении амплитуды возможно движение с подбрасыванием со скоростями V = 20–25 м/мин.
Принцип вибрационного перемещения находит широкое применение в вибрационных загрузочных и транспортных устройствах.
1 – бункер; 2 – прокладка; 3 – якорь;
4 – подвеска; 5 – вибратор; 6 – ось;
7 – амортизатор; 9 – лоток;
10 – обечайка; 11 – конус; 12 – днище;
13 – катушка; 14 – сердечник; 15 – плита;
16 – основание
Слайд 6Тема 7
7.7. Механический КПД механизмов и машин
Коэффициент полезного действия (КПД) −
Тема 7
7.7. Механический КПД механизмов и машин
Коэффициент полезного действия (КПД) −

В период установившегося движения соблюдается условие равенства работ движущих сил и сил сопротивлений
Адв= Ас.
Работа сил сопротивления складывается из суммы сил полезного сопротивления, т. е. тех сил, для преодоления которых предназначен механизм или машина, и сил вредного сопротивления, к которым относятся силы трения, силы аэрогидродинамического сопротивления и т. д.
Адв= Апс + Атр.
Количественно КПД определяется отношением работы сил полезного сопротивления к работе движущих сил
Выразим работу сил полезного сопротивления
Апс = Адв − Атр.
Слайд 7Тема 7
Тогда
где коэффициент потерь, который показывает, какая часть работы движущих
Тема 7
Тогда
где коэффициент потерь, который показывает, какая часть работы движущих

Коэффициент полезного действия (КПД) механизма всегда меньше единицы, так как так как коэффициент потерь не может быть равен нулю из-за потерь механической энергии, вызванных наличием трения в кинематических парах
Чем ближе значение КПД к единице, тем меньше потери, следовательно, выше качество механизма или машины.
Каждая машина представляет собой комплекс механизмов, соединенных последовательно или параллельно. Поэтому общий КПД можно вычислить по отдельным ее элементам.
Слайд 8Тема 7
Последовательное соединение механизмов
Рассмотрим машину, состоящую из последовательно соединенных механизмов, условно
Тема 7
Последовательное соединение механизмов
Рассмотрим машину, состоящую из последовательно соединенных механизмов, условно
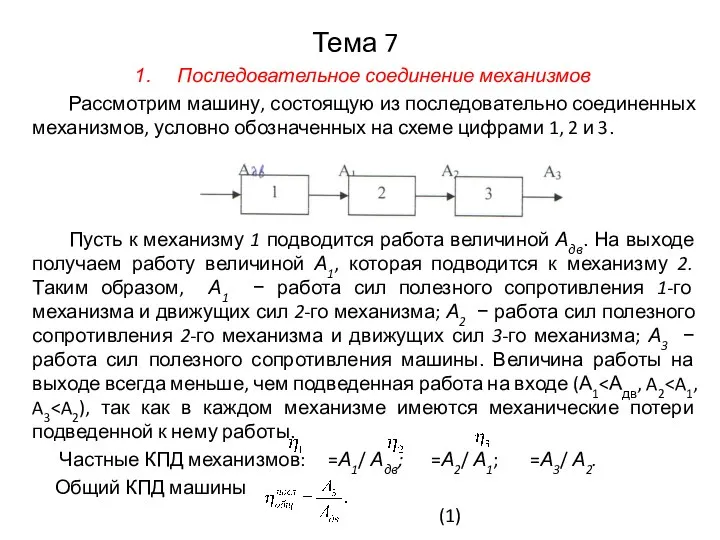
Пусть к механизму 1 подводится работа величиной Адв. На выходе получаем работу величиной А1, которая подводится к механизму 2. Таким образом, А1 − работа сил полезного сопротивления 1-го механизма и движущих сил 2-го механизма; А2 − работа сил полезного сопротивления 2-го механизма и движущих сил 3-го механизма; А3 − работа сил полезного сопротивления машины. Величина работы на выходе всегда меньше, чем подведенная работа на входе (А1<Адв, A2
Общий КПД машины
(1)
Слайд 9Тема 7
Найдем произведение частных КПД
(2)
Сравнивая (1) и (2), можно
Тема 7
Найдем произведение частных КПД
(2)
Сравнивая (1) и (2), можно

Здесь n – число механизмов.
2. Параллельное соединение механизмов
Рассмотрим машину, состоящую из трех параллельно соединенных механизмов, условно обозначенных на схеме цифрами 1, 2, 3.
Пусть к механизмам подводится работа
величиной Адв, которая распределяется на
каждый механизм в разных долях,
определяемых коэффициентами а1, а2, а3,
каждый из которых меньше 1, а их сумма
а1 + а2 + а3 = 1.
Слайд 10Тема 7
Общий КПД машины
(3)
Так как
Подставив эти выражения в (3),
Тема 7
Общий КПД машины
(3)
Так как
Подставив эти выражения в (3),

Отсюда следует, что общий механический КПД машины при параллельном соединении механизмов равен сумме величин КПД каждого механизма, умноженных на коэффициенты долей работ, подводимых к механизмам:
Здесь а1 + а2 + а3 + …. + аn = 1.
Слайд 11Тема 7
Сравним варианты последовательного и параллельного соединения механизмов с точки зрения
Тема 7
Сравним варианты последовательного и параллельного соединения механизмов с точки зрения

При этом коэффициенты, учитывающие доли распределения общей работы Адв между всеми механизмами, также равны:
Тогда
Так как η < 1, то η3 < η. Отсюда следует, что параллельное соединение механизмов в машине предпочтительнее с точки зрения уменьшения механических потерь.
Слайд 12Тема 8
Тема 8. Введение в динамику машин
8.1. Основные задачи и методы динамики
Тема 8
Тема 8. Введение в динамику машин
8.1. Основные задачи и методы динамики

Динамика – это раздел дисциплины «Теории механизмов и машин», изучающий методы исследования движения механизмов и машин, происходящего под действием приложенных сил и моментов пар сил в функции времени.
В динамике машин решаются две основные задачи: прямая задача (задача динамического анализа), заключающаяся в определении законов движения рабочих органов механизмов и машин по заданным силам; обратная задача (задача динамического синтеза), состоящая в нахождении силовых воздействий, обеспечивающих воспроизведение заданных законов движения.
Кроме того, в процессе динамических исследований могут определяться мощности, необходимые для обеспечения заданного режима движения машины; проводиться сравнительная оценка механизмов и машин с учетом их механического коэффициента полезного действия; устанавливаться законы движения ведущего звена (например, колебания угловой скорости кривошипа за один оборот) под действием внешних сил, приложенных к звеньям механизма; а также решаться задачи динамической балансировки, виброзащиты и виброизоляции или подбора оптимальных соотношений между силами, массами и размерами звеньев механизмов.
Слайд 13Тема 8
Объектом изучения в динамике машин является машинный агрегат. В общем
Тема 8
Объектом изучения в динамике машин является машинный агрегат. В общем

В качестве основного метода динамического исследования механизмов и машин положен закон сохранения энергии, сформулированный М.В. Ломоносовым. Последний удобно записать в форме теоремы об изменении кинетической энергии: изменение кинетической энергии механизма на некотором перемещении равно разности работ движущих сил и сил сопротивления движению на этом перемещении
T – T0 = Адв – Ас ,
где T0 – кинетическая энергия в начале движения; T – кинетическая энергия в конце движения; Адв – работа движущих сил; Ас – работа сил сопротивления.
Приведенное равенство и будет основным уравнением движения механизма.
Наряду с этим уравнением и ранее применявшемся при силовом анализе механизмов принципом Даламбера, в динамике машин используются уравнения Лагранжа второго рода, уравнения Аппеля, принцип наименьшего принуждения Гаусса и другие уравнения и принципы, известные из теоретической механики.
Таким образом, зная силы, действующие в машине или механизме, нетрудно определить и работу этих сил, а зная массу движущихся звеньев можно определить и их кинетическую энергию.
Слайд 14Тема 8
Работа – это физическая величина, характеризующая преобразование энергии из одной формы в
Тема 8
Работа – это физическая величина, характеризующая преобразование энергии из одной формы в

Элементарная работа силы выражается формулой
dA = F ⋅ dS ⋅ cos α ,
где F – сила; dS – элементарная величина перемещения точки приложения силы; α – угол между направлениями силы и перемещения.
Элементарная работа момента силы выражается формулой
dA = M ⋅ dφ,
где М – момент силы; dφ – элементарный угол поворота.
Полная работа выражается формулами
A = ∫dA = ∫F cosα dS или A = ∫M dφ.
Мощность – это характеристика скорости изменения энергии, которая определяется как производная работы по времени.
где αi – угол между направлениями векторов силы и скорости.
В случае действия постоянных сил используется значение средней мощности – это отношение совершенной работы к интервалу времени ее выполнения.
N = P ⋅ V ⋅ cos α или N = M ⋅ ω.
Слайд 15Тема 8
Кинетическая энергия – это накопленная работа, совершаемая
над механической системой с целью сообщения
Тема 8
Кинетическая энергия – это накопленная работа, совершаемая над механической системой с целью сообщения

Для i-го звена, совершающего сложное движение (например, для шатуна кривошипно-ползунного механизма), кинетическую энергию можно выразить как сумму кинетических энергий поступательного движения со скоростью центра масс звена и вращательного движения вокруг оси, проходящей через центр масс и перпендикулярной плоскости движения
где mi – масса i-ого звена; Vsi – скорость центра масс i-ого звена; Jsi – момент инерции i-ого звена относительно его центра масс; ωi – угловая скорость i-ого звена; r – число звеньев, совершающих вращательное движение.
Для всего механизма кинетическая энергия равна сумме кинетических энергий всех звеньев
где n – количество подвижных звеньев.
Слайд 16Тема 8
8.2. Выбор динамической модели машинного агрегата
Машинные агрегаты являются сложными многозвенными
Тема 8
8.2. Выбор динамической модели машинного агрегата
Машинные агрегаты являются сложными многозвенными

Выбор той или иной динамической модели машинного агрегата определяется, прежде всего, характером исследуемых процессов: скоростью изменения выходных координат, частотным спектром действующих в машине активных сил и т. п. В значительной степени выбор адекватной модели является эвристической процедурой, основанной, в первую очередь, на опыте конструктора. С одной стороны, динамическая модель должна быть достаточно простой, чтобы обеспечить практическую осуществимость и эффективность решения задач динамики а, с другой стороны, достаточно сложной, чтобы гарантировать достоверность получаемых на её основе результатов.
Слайд 17Тема 8
Во всех случаях следует стремиться к использованию наиболее простых динамических
Тема 8
Во всех случаях следует стремиться к использованию наиболее простых динамических

Наибольшее применение в динамике машин получила одномассовая динамическая модель, т.е. расчетная схема с одним звеном (звеном приведения), координата (и её производные) которого совпадают с обобщенной координатой (и её производными) механизма в любой момент времени.
Эта расчетная схема, при всей своей простоте, отражает многие характерные особенности поведения машинных агрегатов с жесткими звеньями. Учет упругих свойств звеньев приводит к необходимости применения более сложных двухмассовых и многомассовых расчетных схем.
Для получения динамических моделей машинных агрегатов используется метод приведения сил и масс к какому-либо звену механизма.
Слайд 18Тема 8
В качестве звена приведения целесообразно выбрать такое, которое не изменяет
Тема 8
В качестве звена приведения целесообразно выбрать такое, которое не изменяет

Для того, чтобы движение реального механизма или машины было эквивалентным движению динамической модели, необходимо выполнение следующих условий (условий приведения):
1. Кинетическая энергия звена приведения должна быть равна сумме кинетических энергий всех звеньев механизма или машины;
2. Работа или мощность условных сил, приложенных к звену приведения, должна быть равна сумме работ или мощностей всех реальных внешних сил и моментов сил, действующих на механизм или машину.
Таким образом, работу всех внешних сил, действующих в механизме, можно заменить работой одной приведенной силы или момента силы, а кинетическую энергию всех звеньев механизма — соответственно кинети-ческой энергией приведенной массы или приведенного момента инерции.
Слайд 19Тема 8
8.3. Приведение сил и моментов сил
Определим значения приведенных сил и
Тема 8
8.3. Приведение сил и моментов сил
Определим значения приведенных сил и

Для этого воспользуемся вторым условием приведения, согласно которому для сохранения эквивалентности динамической модели реальному механизму работа или мощность условных сил или моментов сил, приложенных к звену приведения, должна быть равна сумме работ или мощностей всех реальных внешних сил и моментов сил, действующих на механизм
(1)
где Nп – мощность приведенной силы; Ni – мощность внешней силы; Fi – внешняя сила; Vi – скорость точки приложения внешней силы; αi – угол между векторами внешней силы и скорости точки её приложения; Mi – момент пары сил, приложенных к звену; ωi – угловая скорость звена; n – число подвижных звеньев.
Слайд 20Тема 8
Пусть звено приведения совершает поступательное движение. Тогда
Nп=Fп•VA ,
где Fп
Тема 8
Пусть звено приведения совершает поступательное движение. Тогда
Nп=Fп•VA ,
где Fп

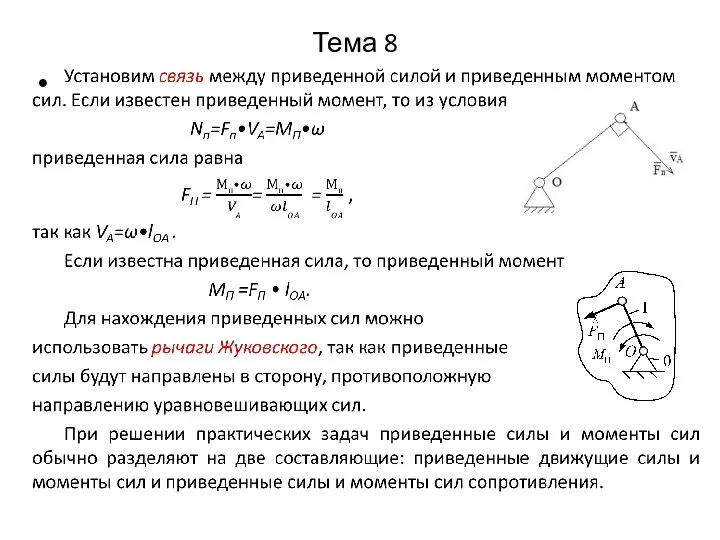
Подставляя это выражение в (1), получим
FП = NП /VA = / VA = ( Fi Vi cos αi / VA + Mi ωi). (2)
Приведенной силой называется такая условная сила, приложенная к звену приведения, работа или мощность которой равна сумме работ или мощностей всех внешних сил и моментов сил, действующих на звенья механизма.
Если звено приведения совершает вращательное движение, то
Nп=Mп•ω ,
где Mп – приведенный момент сил; ω – угловая скорость
звена приведения.
Подставляя это выражение в (1), получим
MП = NП / ω = / ω = ( Fi Vi cos αi / ω + Mi ωi / ω). (3)
Приведенным моментом сил называется такой условный момент, приложенный к звену приведения, работа или мощность которого равна сумме работ или мощностей всех внешних сил и моментов сил, действующих на звенья механизма.
Слайд 21Тема 8
Тема 8
Слайд 22Тема 8
8.4. Приведение масс и моментов инерции
Для нахождения приведенных масс
Тема 8
8.4. Приведение масс и моментов инерции
Для нахождения приведенных масс

ТП = Ti, (4)
где ТП – кинетическая энергия звена приведения; Ti – кинетическая энергия i-того звена; n – число подвижных звеньев.
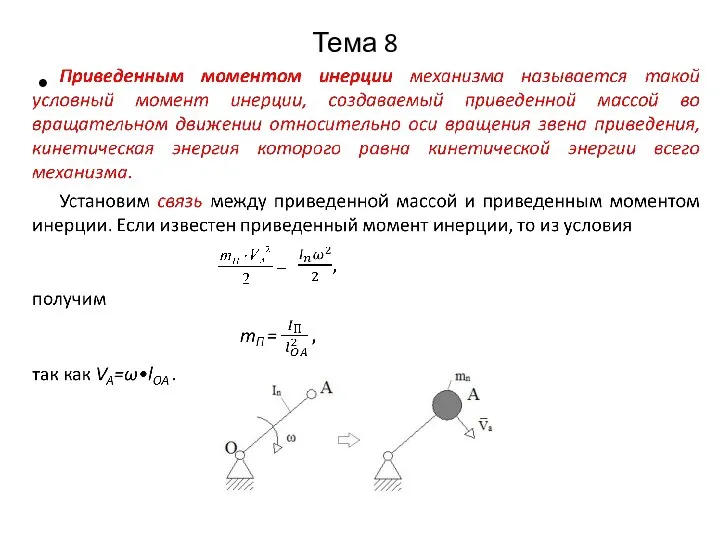
Пусть звено приведения совершает поступательное движение. Тогда
TП = mП VA2/2,
где mП – приведенная масса; VA – скорость т. А звена.
Кинетическая энергия всех звеньев механизма
Подставляя эти выражения в (4), получим
Слайд 23Тема 8
Тема 8

Слайд 24Тема 8
Тема 8
Слайд 25Тема 8
Тема 8
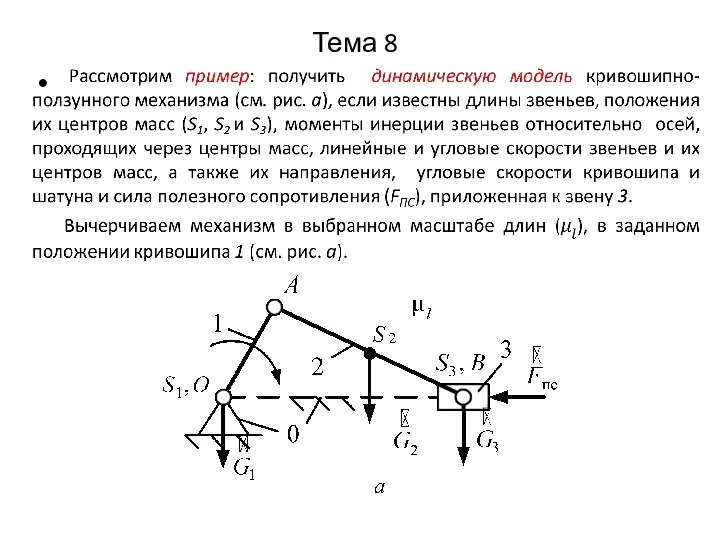
Слайд 26Тема 8
Тема 8

Слайд 27Тема 8
8.5. Режимы движения машинных агрегатов и их энергетические характеристики
Полным временем
Тема 8
8.5. Режимы движения машинных агрегатов и их энергетические характеристики
Полным временем
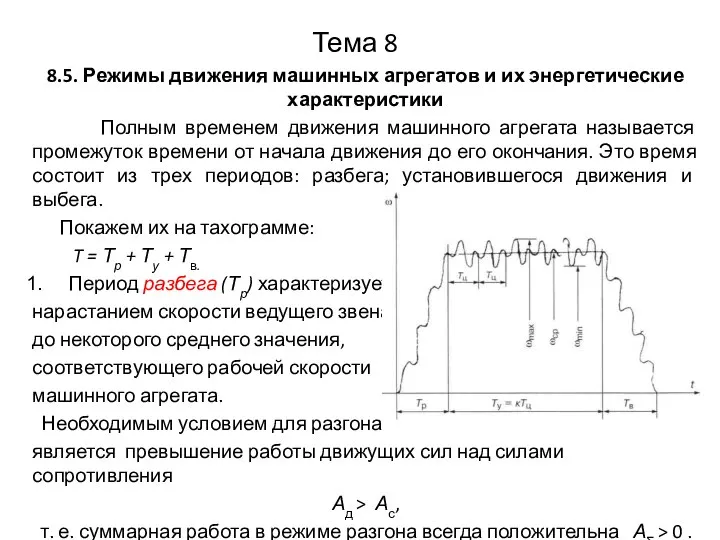
Покажем их на тахограмме:
T = Тр + Ту + Тв.
Период разбега (Тр) характеризуется
нарастанием скорости ведущего звена
до некоторого среднего значения,
соответствующего рабочей скорости
машинного агрегата.
Необходимым условием для разгона
является превышение работы движущих сил над силами сопротивления
Ад > Ас,
т. е. суммарная работа в режиме разгона всегда положительна АΣ > 0 .
Слайд 28Тема 8
2. Период установившегося движения
(Ту) – период движения, при котором
угловая скорость
Тема 8
2. Период установившегося движения
(Ту) – период движения, при котором
угловая скорость
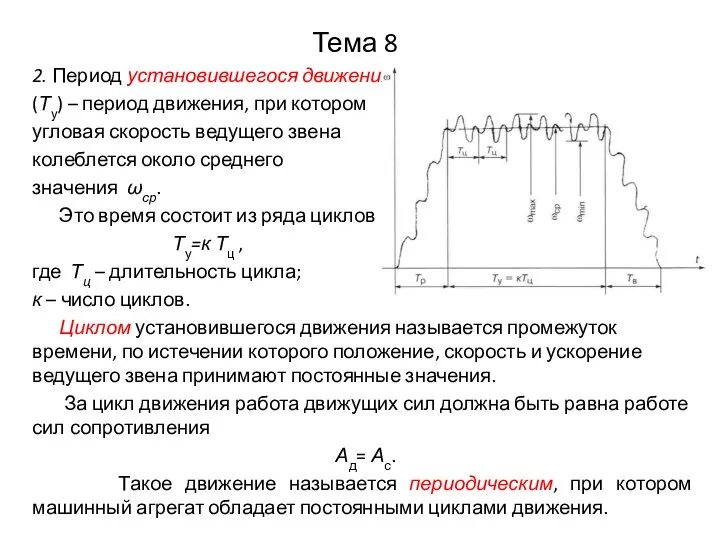
колеблется около среднего
значения ωср.
Это время состоит из ряда циклов
Ту=к Тц ,
где Тц – длительность цикла;
к – число циклов.
Циклом установившегося движения называется промежуток времени, по истечении которого положение, скорость и ускорение ведущего звена принимают постоянные значения.
За цикл движения работа движущих сил должна быть равна работе сил сопротивления
Ад= Ас.
Такое движение называется периодическим, при котором машинный агрегат обладает постоянными циклами движения.
Слайд 29Тема 8
3. Период выбега или остановки (Тв) –
период времени, в течение
Тема 8
3. Период выбега или остановки (Тв) –
период времени, в течение
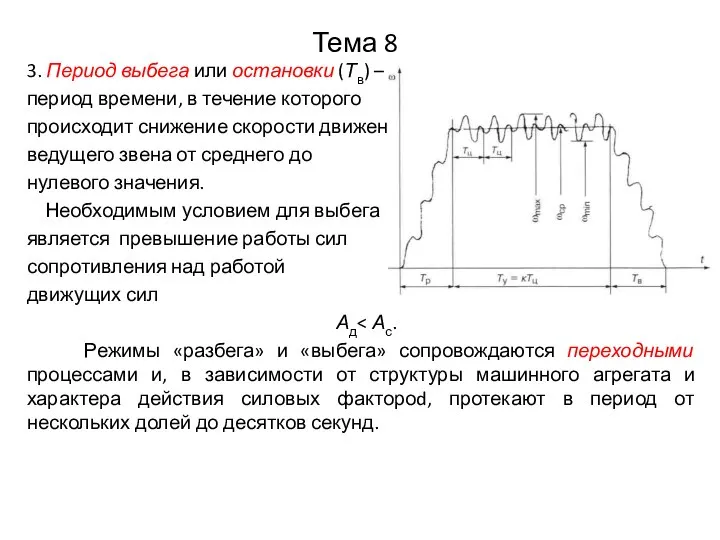
происходит снижение скорости движения
ведущего звена от среднего до
нулевого значения.
Необходимым условием для выбега
является превышение работы сил
сопротивления над работой
движущих сил
Ад< Ас.
Режимы «разбега» и «выбега» сопровождаются переходными процессами и, в зависимости от структуры машинного агрегата и характера действия силовых фактороd, протекают в период от нескольких долей до десятков секунд.
Слайд 30Тема 8
Исследование переходных режимов необходимо для нахождения времени срабатывания машинного агрегата,
Тема 8
Исследование переходных режимов необходимо для нахождения времени срабатывания машинного агрегата,

Стремление к повышению производительности этих устройств может привести к возникновению больших ускорений, вызывающих значительные динамические нагрузки и упругие колебания исполнительных механизмов, которые нарушают точность функционирования, увеличивают время выполнения операций и снижают прочность основных элементов и надежность работы. Таким образом, при создании подобных машин возникает задача учета упругих свойств конструкции и разработки методов и средств ограничения колебательных движений. Кроме того, в периоды разбега и выбега необходимо решать проблему прохода через критические зоны, когда угловая скорость ведущего вала машинного агрегата становится равной одной из собственных частот колебаний, при которых механическая система попадает в резонанс, длительное пребывание в котором может привести к разрушению конструкции.
Слайд 31Тема 8
В режиме установившегося движения работает большинство технологических и энергетических машин:
Тема 8
В режиме установившегося движения работает большинство технологических и энергетических машин:

За цикл установившегося движения изменение кинетической энергии равно нулю (ΔT = 0). Однако внутри цикла угловая скорость ведущего звена может меняться из-за несовпадения законов изменения движущих сил и сил сопротивления, а также непостоянства значений приведенного момента инерции машинного агрегата. Например, для механизмов станков и поршневых насосов и компрессоров приведенный момент движущих сил является постоянной величиной, а приведенный момент сил сопротивления − переменной. Для механизмов двигателей внутреннего сгорания и паровых машин постоянным является приведенный момент сил сопротивления, а переменным − приведенный момент движущих сил. Приведенный момент инерции машинного агрегата также является переменной величиной при изменении положений ведущего звена. В результате этого значение скорости движения его ведущего звена колеблется в течение рассматриваемого промежутка времени в некотором диапазоне от максимума до минимума.

 Материальная точка. Система отсчета
Материальная точка. Система отсчета Массовая доля растворённого вещества
Массовая доля растворённого вещества Что изучает физика
Что изучает физика Машиноведение. Строение машинной иглы, регулятора длины стежка. Уход за швейной машиной
Машиноведение. Строение машинной иглы, регулятора длины стежка. Уход за швейной машиной Il modello atomico di Schrödinger
Il modello atomico di Schrödinger Измерение объема
Измерение объема Короткое замыкание
Короткое замыкание Электрические явления в природе: молнии
Электрические явления в природе: молнии Презентация на тему Механическая работа. Мощность 7 класс
Презентация на тему Механическая работа. Мощность 7 класс  Поступательное и вращательное движение тел
Поступательное и вращательное движение тел Презентация на тему Магнетизм
Презентация на тему Магнетизм  Белаз 7519
Белаз 7519 Второе начало термодинамики
Второе начало термодинамики Механические колебания
Механические колебания Изобретения, облегчающие жизнь людям с ограниченными возможностями
Изобретения, облегчающие жизнь людям с ограниченными возможностями Lektsia_Volny_ZS
Lektsia_Volny_ZS Основные детали остова двигателя. Станина и цилиндры. Картеры, крепление. Вентиляция. Урок № 7. Тема 2.4
Основные детали остова двигателя. Станина и цилиндры. Картеры, крепление. Вентиляция. Урок № 7. Тема 2.4 Стартовый ускоритель
Стартовый ускоритель Общий курс железных дорог. ОКЖД. Лекция 1
Общий курс железных дорог. ОКЖД. Лекция 1 Количество теплоты. Удельная теплоёмкость
Количество теплоты. Удельная теплоёмкость Презентация на тему Трансформатор. Передача электрической энергии на расстояние
Презентация на тему Трансформатор. Передача электрической энергии на расстояние  Понятие поглощенной дозы. Понятие эквивалентной дозы. Единицы измерения поглощенной и эквивалентной дозы
Понятие поглощенной дозы. Понятие эквивалентной дозы. Единицы измерения поглощенной и эквивалентной дозы Движение в неинерциальных системах отсчёта
Движение в неинерциальных системах отсчёта Закон сохранения энергии
Закон сохранения энергии Антенна. Классификация радиопередающих устройств
Антенна. Классификация радиопередающих устройств Формула бинома Ньютона. Свойства биноминальных коэффициентов
Формула бинома Ньютона. Свойства биноминальных коэффициентов 50_ottenkov_sinego
50_ottenkov_sinego Технология проверки технического состояния направляющих и ведущих колёс
Технология проверки технического состояния направляющих и ведущих колёс