Содержание
- 2. Карта презентации.
- 3. Блокнот. 1. x y z = (x+ky)/(k+1), где k= x1/ y1 z x1 y1 2. -
- 4. Краткие биографические сведения о Леонардо Эйлере. Идеальный математик 18 века - так часто называют Эйлера(1707-1789). Он
- 5. Прямая Эйлера. Дан прямоугольный треугольник АСВ. Проведем медиану СО. Середина O гипотенузы AB является центром описанной
- 6. Прямая Эйлера. Деление отрезка в данном отношении.
- 7. Прямая Эйлера
- 8. Прямая Эйлера
- 9. Прямая Эйлера
- 10. Прямая Эйлера Задача Какие стороны пересекает прямая Эйлера в остроугольном и тупоугольном треугольниках? Решение Пусть AB
- 11. Теорема Эйлера о многогранниках. (4)Теорема Эйлера: Пусть В - число вершин выпуклого многогранника, Р - число
- 12. Теорема Эйлера о многогранниках. Имеется много доказательств теоремы Эйлера. В одной из них используется формула для
- 13. Доказательство: Перепишем соотношение Эйлера дважды, один раз в виде Р + 2 = В + Г
- 14. Теорема Эйлера о многогранниках. Задача. Доказать теорему Эйлера для плоского графа. (Граф называется плоским, если его
- 15. Теория графов и задача Эйлера. Издавна среди жителей Кёнигсберга была распространена такая загадка: как пройти по
- 16. Теория графов и задача Эйлера. Теорема Эйлера. (5) Пусть на плоскости задано m точек и n
- 18. Скачать презентацию
Слайд 3Блокнот.
1.
x
y
z = (x+ky)/(k+1), где k= x1/ y1
z
x1
y1
2.
- центроид
3d=a+b+c
3.
- ортоцентр
- Центр описанной окружности
d=a+b+c
4.
Для
Блокнот.
1.
x
y
z = (x+ky)/(k+1), где k= x1/ y1
z
x1
y1
2.
- центроид
3d=a+b+c
3.
- ортоцентр
- Центр описанной окружности
d=a+b+c
4.
Для
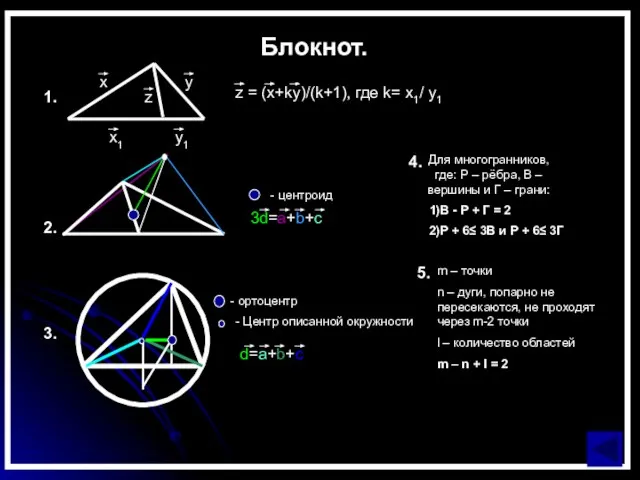
1)В - Р + Г = 2
2)Р + 6≤ 3В и Р + 6≤ 3Г
m – точки
n – дуги, попарно не пересекаются, не проходят через m-2 точки
l – количество областей
m – n + l = 2
5.
Слайд 4Краткие биографические сведения о Леонардо Эйлере.
Идеальный математик 18 века - так
Краткие биографические сведения о Леонардо Эйлере.
Идеальный математик 18 века - так

В 26 лет Эйлер был избран российским академиком, но через 8 лет он переехал из Петербурга в Берлин. Там "король математиков" работал с 1741 по 1766 год; потом он покинул Берлин и вернулся в Россию. Удивительно: слава Эйлера не закатилась и после того, как ученого поразила слепота (вскоре после переезда в Петербург). В 1770-е годы вокруг Эйлера выросла Петербургская математическая школа, более чем наполовину состоявшая из русских ученых. Тогда же завершилась публикация главной его книги - "Основ дифференциального и интегрального исчисления".
В начале сентября 1783 Эйлер почувствовал легкое недомогание. 18 сентября он еще занимался математическими исследованиями, но неожиданно потерял сознание и «прекратил вычислять и жить».
Похоронен на Смоленском лютеранском кладбище в Петербурге, откуда его прах перенесен осенью 1956 в некрополь Александро-Невской лавры.
Л. Эйлер
Слайд 5Прямая Эйлера.
Дан прямоугольный треугольник АСВ. Проведем медиану СО. Середина O гипотенузы AB
Прямая Эйлера.
Дан прямоугольный треугольник АСВ. Проведем медиану СО. Середина O гипотенузы AB
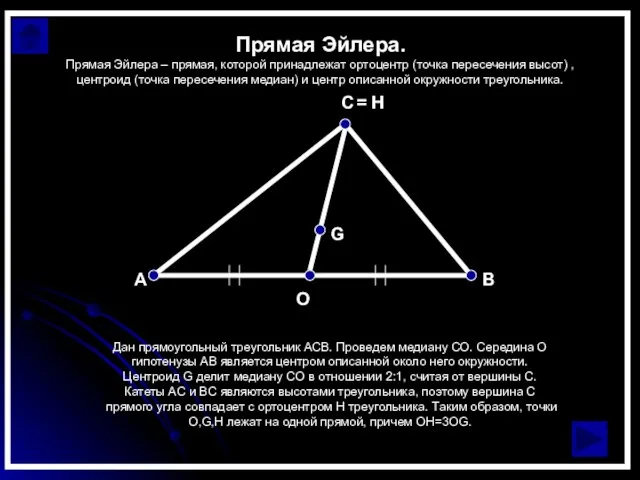
Прямая Эйлера – прямая, которой принадлежат ортоцентр (точка пересечения высот) , центроид (точка пересечения медиан) и центр описанной окружности треугольника.
= Н
Слайд 6Прямая Эйлера.
Деление отрезка в данном отношении.
Прямая Эйлера.
Деление отрезка в данном отношении.
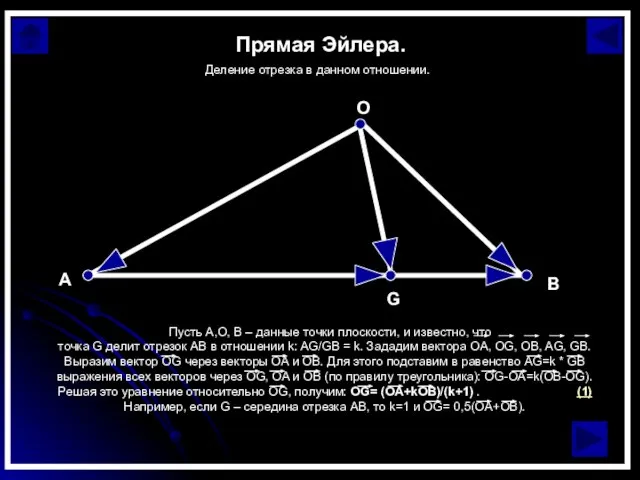
Слайд 7Прямая Эйлера
Прямая Эйлера
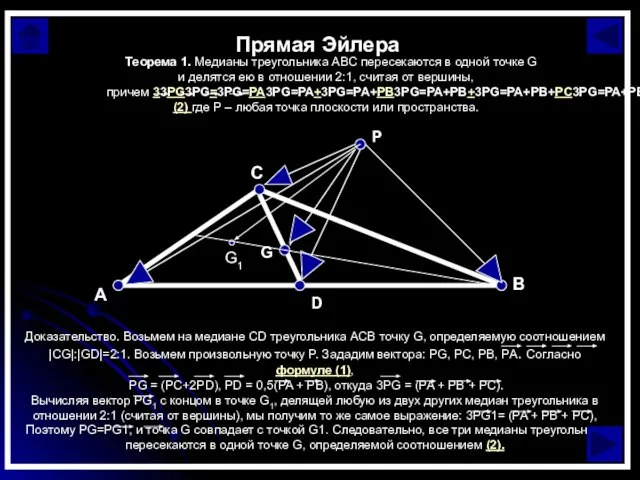
Слайд 8Прямая Эйлера
Прямая Эйлера

Слайд 9Прямая Эйлера
Прямая Эйлера
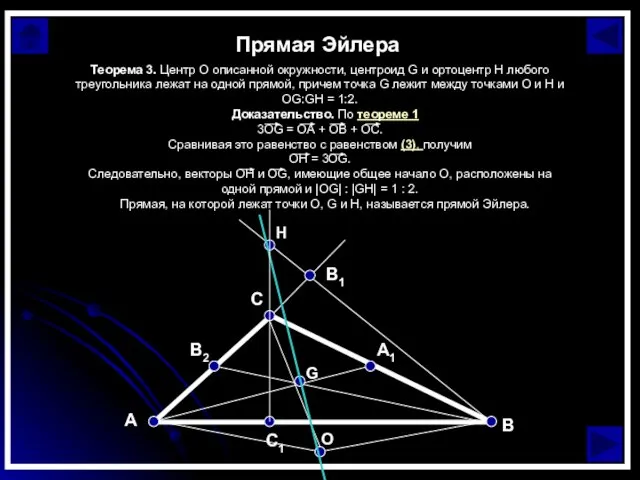
Слайд 10Прямая Эйлера
Задача
Какие стороны пересекает прямая Эйлера в остроугольном и тупоугольном треугольниках?
Решение
Пусть AB >
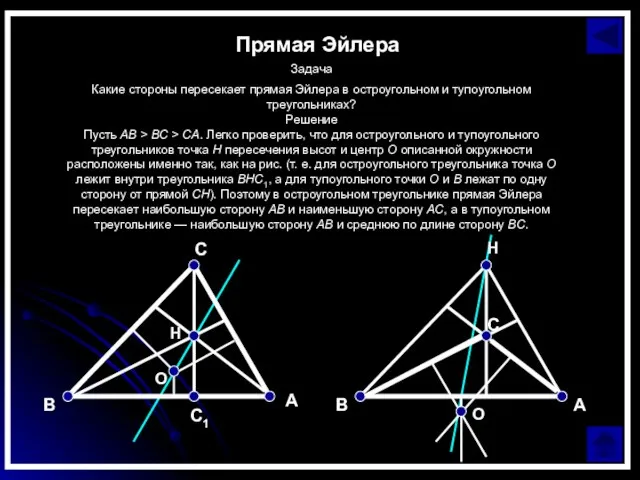
Прямая Эйлера
Задача
Какие стороны пересекает прямая Эйлера в остроугольном и тупоугольном треугольниках?
Решение
Пусть AB >
Слайд 11Теорема Эйлера о многогранниках.
(4)Теорема Эйлера:
Пусть В - число вершин выпуклого многогранника,
Теорема Эйлера о многогранниках.
(4)Теорема Эйлера: Пусть В - число вершин выпуклого многогранника,

В - Р + Г = 2
Число х = В - Р + Г называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого многогранника эта характеристика равна 2. То, что эйлеровая характеристика равна 2 для многих многогранников, видно из следующей таблицы:
Многогранник
В
Р
Г
Х
Тетраэдр
Куб
n-угольная
пирамида
n-угольная
призма
4
6
4
8
12
6
n+1
2n
n+1
2n
3n
n+2
2
2
2
2
Слайд 12Теорема Эйлера о многогранниках.
Имеется много доказательств теоремы Эйлера. В одной из них
Теорема Эйлера о многогранниках.
Имеется много доказательств теоремы Эйлера. В одной из них

F
Слайд 13Доказательство:
Перепишем соотношение Эйлера дважды, один раз в виде
Р + 2
Доказательство:
Перепишем соотношение Эйлера дважды, один раз в виде
Р + 2

И другой раз в виде
4 = 2В - 2Р + 2Г
Складывая эти равенства, получаем
Р + 6 = 3В + 3Г - 2Р
Так как у каждой грани многогранника не менее трех сторон, то 3Г≤ 2Р. Отсюда сразу получаем Р + 6≤ 3В.
Утверждение доказано.
Доказательство:
Обозначим через Гi число i-угольных граней в многограннике М. Ясно, что
Г = Г3 + Г4 + Г5 + …
Ясно также, что каждая i-угольная грань содержит i ребер многогранника. С другой стороны, каждое ребро многогранника принадлежит в точности двум граням. Поэтому в сумме 3Г3 + 4Г4 + 5Г5 + … каждое ребро многогранника подсчитано, причем подсчитано дважды. Отсюда имеем
2Р = 3Г3 + 4Г4 + 5Г5 +…
Рассмотрим теперь сумму S плоских углов многогранника:
S = Г3 ·π + Г4 · 2π + Гi · ( i -2 )π + …
С учетом полученных соотношений и теоремы Эйлера соотношение можно переписать так:
S = Г3 ( 3 - 2 )π + Г4 (4 -2 )π + Гi ( i - 2 )π + … = 2Рπ - 2Гπ = 2Вπ - 4π.
Слайд 14Теорема Эйлера о многогранниках.
Задача. Доказать теорему Эйлера для плоского графа. (Граф называется
Теорема Эйлера о многогранниках.
Задача. Доказать теорему Эйлера для плоского графа. (Граф называется

Если в графе есть цикл, то есть внутренняя грань. Возьмем цикл, ограничивающий внутреннюю грань. Выкинем из него одно ребро. Граф остался связным, плоским. Число Р уменьшилось на один, но и число Г уменьшилось на один, т.к. грань, которая была по сторону от стертого ребра стерлась. Таким образом, число В+Г-Р не изменилось. Если в графе опять есть цикл мы поступаем так же. Т.к. ребер в графе конечное число, а количество ребер постепенно уменьшается, то когда-нибудь наше стирание его рёбер закончится. Т.е. мы придем к ситуации, что число В+Г-Р не изменилось по сравнению с первоначальным, граф остался связным, плоским и циклов в графе нет. => граф стал деревом, а грань осталась одна - внешняя. Продолжаем стирать грани. Число Р уменьшается на один, число В уменьшается на один, число В+Г-Р не меняется. Полученный граф снова дерево, он плоский и связный, а число вершин у него уменьшилось => поступаем так, пока не останется две вершины, соединенные ребром. Тут уже не сложно посчитать, что В+Г-Р=2+1-1=2, а число В+Г-Р не менялось => для начального графа оно тоже 2.
Слайд 15Теория графов и задача Эйлера.
Издавна среди жителей Кёнигсберга была распространена такая загадка:
Теория графов и задача Эйлера.
Издавна среди жителей Кёнигсберга была распространена такая загадка:
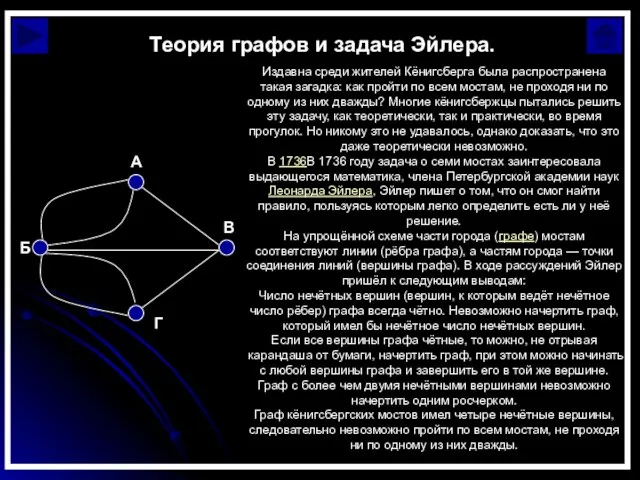
В 1736В 1736 году задача о семи мостах заинтересовала выдающегося математика, члена Петербургской академии наук Леонарда Эйлера, Эйлер пишет о том, что он смог найти правило, пользуясь которым легко определить есть ли у неё решение.
На упрощённой схеме части города (графе) мостам соответствуют линии (рёбра графа), а частям города — точки соединения линий (вершины графа). В ходе рассуждений Эйлер пришёл к следующим выводам:
Число нечётных вершин (вершин, к которым ведёт нечётное число рёбер) графа всегда чётно. Невозможно начертить граф, который имел бы нечётное число нечётных вершин.
Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине.
Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком.
Граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно невозможно пройти по всем мостам, не проходя ни по одному из них дважды.
Слайд 16Теория графов и задача Эйлера.
Теорема Эйлера. (5)
Пусть на плоскости задано m точек
Теория графов и задача Эйлера.
Теорема Эйлера. (5)
Пусть на плоскости задано m точек
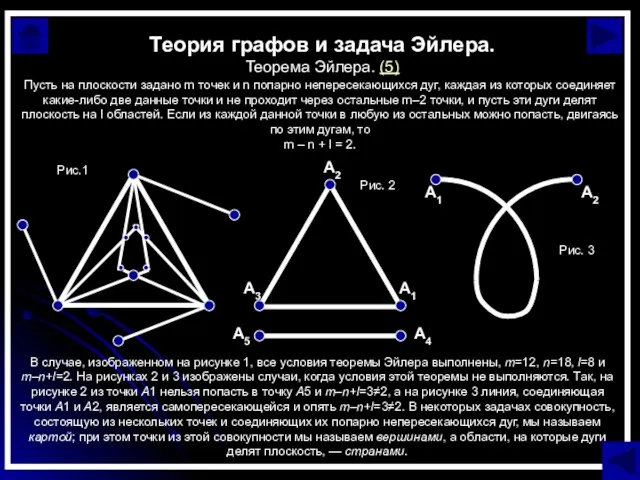
m – n + l = 2.
В случае, изображенном на рисунке 1, все условия теоремы Эйлера выполнены, m=12, n=18, l=8 и m–n+l=2. На рисунках 2 и 3 изображены случаи, когда условия этой теоремы не выполняются. Так, на рисунке 2 из точки A1 нельзя попасть в точку A5 и m–n+l=3≠2, а на рисунке 3 линия, соединяющая точки A1 и A2, является самопересекающейся и опять m–n+l=3≠2. В некоторых задачах совокупность, состоящую из нескольких точек и соединяющих их попарно непересекающихся дуг, мы называем картой; при этом точки из этой совокупности мы называем вершинами, а области, на которые дуги делят плоскость, — странами.

 Общественно-активная школа: эффективность и качество.
Общественно-активная школа: эффективность и качество. 197368
197368 С какво свързваш древногръцкото облекло?
С какво свързваш древногръцкото облекло? Презентация на тему Экономика и ее роль в обществе
Презентация на тему Экономика и ее роль в обществе Фотоальбом. Велосипеди
Фотоальбом. Велосипеди Узорочья Севера
Узорочья Севера Цветы для моей семьи
Цветы для моей семьи Открытые горные работы, их элементы и терминология
Открытые горные работы, их элементы и терминология Бизнес инсайт. Продуктивность как система
Бизнес инсайт. Продуктивность как система Где летит птица?
Где летит птица? Итоги 1 полугодия 2010-2011 уч.года
Итоги 1 полугодия 2010-2011 уч.года Творческий проект Кукла своими руками
Творческий проект Кукла своими руками Буквы О-Ё после шипящих и Ц
Буквы О-Ё после шипящих и Ц Формы взаимодействия с семьей (из опыта работы)
Формы взаимодействия с семьей (из опыта работы) КОММУНИКАТИВНАЯ ПОЛИТИКА ХОЛДИНГОВ
КОММУНИКАТИВНАЯ ПОЛИТИКА ХОЛДИНГОВ Государственное регулирование цен на лекарственные средства на региональном уровне и проблемы, возникающие в рамках действующег
Государственное регулирование цен на лекарственные средства на региональном уровне и проблемы, возникающие в рамках действующег Презентация прочитанной книги
Презентация прочитанной книги Филиал ООО компания Тензор. Сфера торгов
Филиал ООО компания Тензор. Сфера торгов Рекуперативный воздухонагреватель, с использованием жидких горючих отходов.
Рекуперативный воздухонагреватель, с использованием жидких горючих отходов. Интерактивно-аналитический онлайн-сервиса Калькулятор процедур
Интерактивно-аналитический онлайн-сервиса Калькулятор процедур Элла Фицджеральд - выдающаяся джазовая певица, актриса 1917-1996
Элла Фицджеральд - выдающаяся джазовая певица, актриса 1917-1996 Места на направление Товароведение
Места на направление Товароведение Праця неповнолітніх
Праця неповнолітніх Прямолинейное распространение света
Прямолинейное распространение света Документовед он-лайн сервис оформления документов Документы для регистрации общества с ограниченной ответственностью за 15 минут.
Документовед он-лайн сервис оформления документов Документы для регистрации общества с ограниченной ответственностью за 15 минут. Как правильно оформить презентацию и web-сайт?
Как правильно оформить презентацию и web-сайт? Капитализм XVIII века. Промышленный переворот в Англии
Капитализм XVIII века. Промышленный переворот в Англии Работать с молодёжью: как?
Работать с молодёжью: как?