Содержание
- 2. Цели и задачи урока Ввести понятие линейной функции Научить находить по формуле значение аргумента и значение
- 3. Определение Функция вида у = k х + b, (k, b- любое число), - называется линейной
- 4. Задания 1. Определите, какие из указанных функций являются линейными: у = 2(х+3) у = (х+2)(х-1) у
- 5. 2. Функции заданы формулами: у = 2х - 7 у = - 0,6х + 13 у
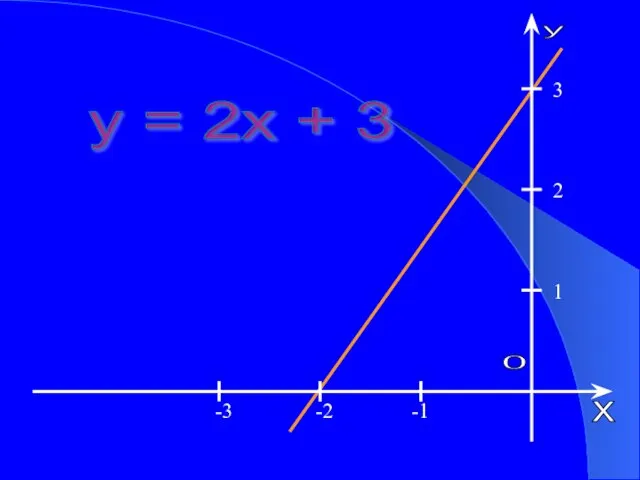
- 6. Построение графика функции График линейной функции – прямая. Для построения прямой достаточно двух точек. Построим график
- 7. y = 2x + 3
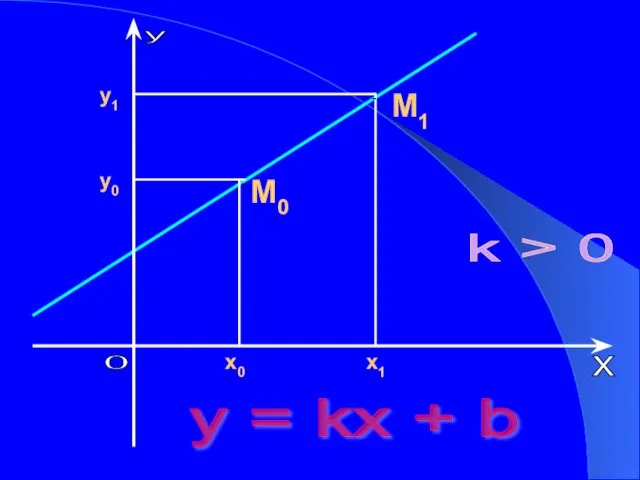
- 8. Свойства функций При k>0, функция возрастает При k При k=0, b не равно нулю, у =
- 9. y = kx + b M1 k > 0
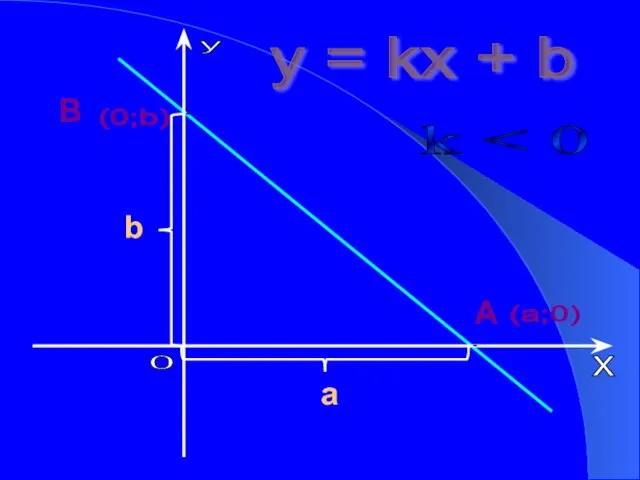
- 10. y = kx + b k
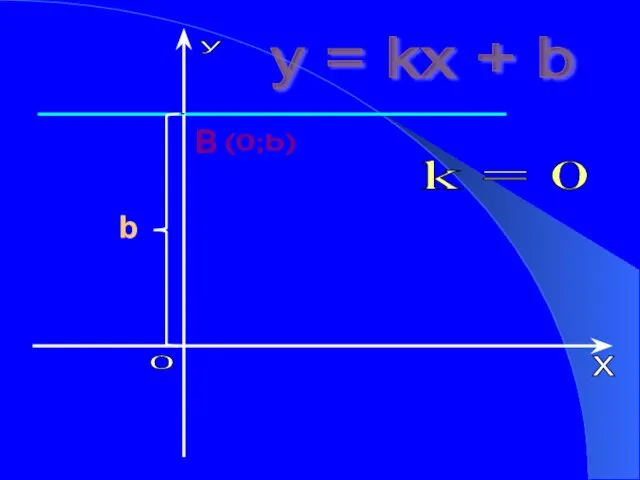
- 11. y = kx + b k = 0
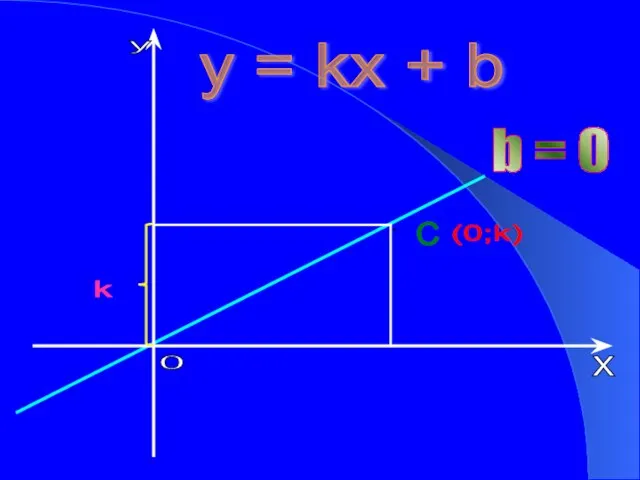
- 12. Графики функции вида у = kх Графики линейных функций вида у = kх (b=0) проходят через
- 13. y = kx + b b = 0
- 14. Вопросы: 1. Когда линейная функция проходит через начало координат? 2. Какая из данных функций возрастает (убывает,
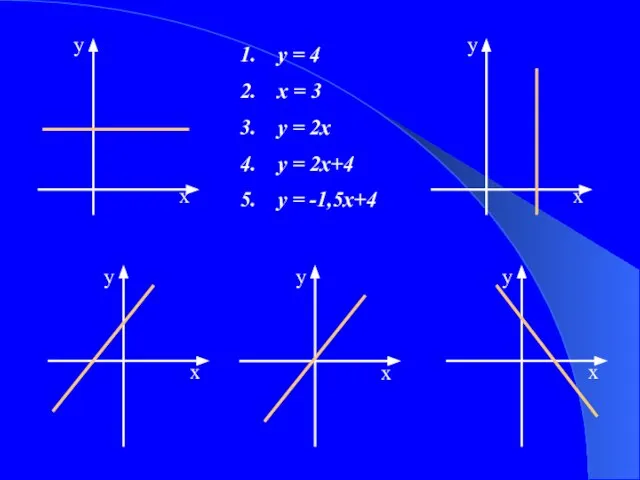
- 15. y = 4 x = 3 у = 2х у = 2х+4 у = -1,5х+4
- 16. Вопросы для повторения Что называется линейной функцией ? Приведите примеры линейных функций. Что является графиком линейной
- 17. 1. Найдите значение функции у = 15х – 1 при х = 2. 2. На одном
- 18. Выводы Применение данного пособия на уроке математики дает: повышение интереса к урокам математики; улучшение дисциплины; улучшение
- 20. Скачать презентацию











 آموزش سواد رسانه ای – درس سوم
آموزش سواد رسانه ای – درس سوم Раскрытие скобок. Линейные уравнения. Повторение
Раскрытие скобок. Линейные уравнения. Повторение История Древнего Рима (МХК 10 класс)
История Древнего Рима (МХК 10 класс) МОДУЛЬНАЯ
МОДУЛЬНАЯ Лучшие инструменты для сведения звука (саундпродюссинг)
Лучшие инструменты для сведения звука (саундпродюссинг) Деловые документы (автобиография, заявление, резюме )
Деловые документы (автобиография, заявление, резюме ) MixMarket.BIZ
MixMarket.BIZ Практика-Инфекции-3 (Бактериальные)
Практика-Инфекции-3 (Бактериальные) природные условия
природные условия Презентация на тему Правописание сочетаний Чк чн
Презентация на тему Правописание сочетаний Чк чн Реконструкция системы водоснабжения п. Гирей, Краснодарского края
Реконструкция системы водоснабжения п. Гирей, Краснодарского края Правила проведения банных процедур
Правила проведения банных процедур Лексические нормы
Лексические нормы Организация общения дошкольников в повседневной жизни и разнообразных видах деятельности
Организация общения дошкольников в повседневной жизни и разнообразных видах деятельности Натюрморт в графике. ИЗО. 6 класс
Натюрморт в графике. ИЗО. 6 класс Каким ты видишь мир?
Каким ты видишь мир? Завоевание Римом Италии 5 класс
Завоевание Римом Италии 5 класс Как продавать продукцию IEK® в розницу: формула успеха
Как продавать продукцию IEK® в розницу: формула успеха Мини-волейбол
Мини-волейбол Подача питательной воды в парогенератор при запроектной аварии
Подача питательной воды в парогенератор при запроектной аварии Мы дарим впечатления, которые хочется хранить всю жизнь!
Мы дарим впечатления, которые хочется хранить всю жизнь! Алгоритм выбора профессии. Занятие 15
Алгоритм выбора профессии. Занятие 15 Crisis del Salitre
Crisis del Salitre The obligation
The obligation  Презентация на тему Что надо знать про жевательную резинку
Презентация на тему Что надо знать про жевательную резинку Анализ сайта Развитие ребёнка
Анализ сайта Развитие ребёнка Производственный комплекс АГАМА
Производственный комплекс АГАМА Современное состояние, перспективы развития общин КМНС. - презентация
Современное состояние, перспективы развития общин КМНС. - презентация