Слайд 2Функцию, заданную формулой
y=logax ,
где а>0, а ≠1
называют логарифмической функцией с основанием а.

Слайд 3Основные свойства функции
y=logax , а>0, а ≠1
D(y)=R+
E(y)=R
Нули: у=0 при х=1
Промежутки знакопостоянства:
при

0<а<1 y>0 при хЄ(0;1);y<0 при хЄ(1;∞);
при а>1 y>0 при хЄ(1;∞);y<0 при хЄ(0;1).
Промежутки монотонности:
при 0<а<1 функция убывает;
при а>1 функция возрастает.
Экстремумы: нет.
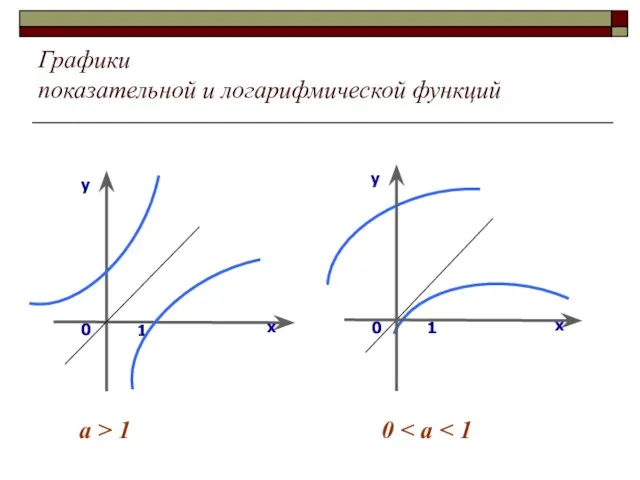
Слайд 5Графики
показательной и логарифмической функций
a > 1
0 < a < 1
Слайд 6Найти область определения функции:
y=log2(х-5)
Область определения логарифмической функции – R+ . Поэтому данная

функция определена для х, при которых х-5>0. Т.о. D(y)=(5;∞)
y=log2sin х
Данная функция определена для х, при которых sin х >0.
Т.о. D(y)=(2πk; π+2πk ), k Є Z
Слайд 7Сравнить:
log37 и log310
Логарифмическая функция с основанием, большим 1,возрастает на всей числовой прямой.

Т.к. 10>7, то log310 > log37 .
log¼7 и log¼10
Логарифмическая функция с основанием, меньшим 1,убывает на всей числовой прямой. Т.к. 7<10, то log¼7 > log¼10.
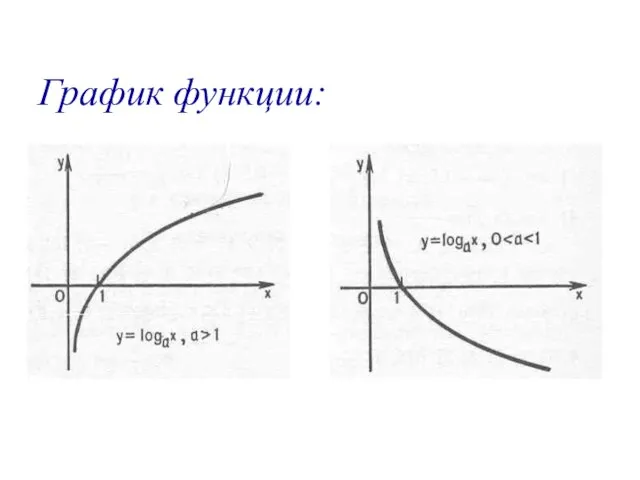
Слайд 8Перечислите основные свойства функции и постройте её график:
y=log3(х-1)
D(y)= (1;∞)
E(y)=R
y=0 при х=2
функция

возрастает
y=log½х+1
D(y)=R+
E(y)=R
y=0 при х=2
функция убывает
Слайд 11Такую кривую описывает движущаяся точка, расстояние от
полюса которой растет в геометрической прогрессии,

а угол,
описываемый ее радиусом-вектором – в арифметической.









 Сбербанк онлайн
Сбербанк онлайн Единицы длины, денежные единицы, меры массы «Счёт и вычисления – основа порядка в голове» И.Песталоцци
Единицы длины, денежные единицы, меры массы «Счёт и вычисления – основа порядка в голове» И.Песталоцци Творческие работы, фотографии
Творческие работы, фотографии Назначение и проведение пожарно-технической экспертизы
Назначение и проведение пожарно-технической экспертизы Arenta. Смарт-офис
Arenta. Смарт-офис Неметаллы
Неметаллы Процесс совершенствования системы управления конфликтами в организации
Процесс совершенствования системы управления конфликтами в организации Понятия коррупция и противодействие коррупции
Понятия коррупция и противодействие коррупции Эскизы мотивов вышивки
Эскизы мотивов вышивки Презентация опыт3
Презентация опыт3 Математик - бизнесмен
Математик - бизнесмен Північна Америка
Північна Америка Традиции и обычаи татар
Традиции и обычаи татар Презентация на тему Кожа и ее значение (4 класс)
Презентация на тему Кожа и ее значение (4 класс) Библиоинновации
Библиоинновации Права потребителя
Права потребителя Образы и мотивы в орнаментах русской народной вышивки (5 класс)
Образы и мотивы в орнаментах русской народной вышивки (5 класс) Корпоративный проект "Сводная база данных "Край":лингвистическое обеспечение
Корпоративный проект "Сводная база данных "Край":лингвистическое обеспечение Степени сравнения прилагательных
Степени сравнения прилагательных Творческое объединение лего-мастерская Шелезяка. Робототехника
Творческое объединение лего-мастерская Шелезяка. Робототехника Основные направления бюджетной и налоговой политики Пермского края на 2018 - 2020-е годы
Основные направления бюджетной и налоговой политики Пермского края на 2018 - 2020-е годы The Rolling Stones
The Rolling Stones  Образ дороги в русской живописи XIX века
Образ дороги в русской живописи XIX века оТЧЕТ о работЕ ШМО учителей математики, информатики, технологии
оТЧЕТ о работЕ ШМО учителей математики, информатики, технологии 20170502_znat_geografiyu-_znachit_pobedit_0
20170502_znat_geografiyu-_znachit_pobedit_0 «ВСЕ В ТВОИХ РУКАХ»
«ВСЕ В ТВОИХ РУКАХ» Древние славяне
Древние славяне Театр масок
Театр масок