Содержание
- 2. — способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется
- 3. - образуется из высказывания с помощью добавления частицы «не» к сказуемому или использования оборота речи «неверно,
- 4. Истинность высказывания, имеющего форму Ā (вне зависимости от его содержания), определяется по специальной таблице истинности. Таблица
- 5. Графическая иллюстрация инверсии с помощью диаграмм Эйлера — Венна: А — множество отличников; Ā — множество
- 6. - образуется соединением двух высказываний в одно с помощью союза «и». Обозначение конъюнкции: A И B;
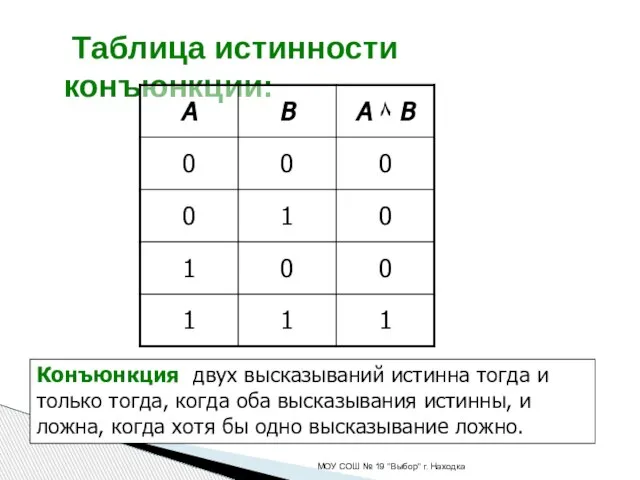
- 7. Таблица истинности конъюнкции: МОУ СОШ № 19 "Выбор" г. Находка Конъюнкция двух высказываний истинна тогда и
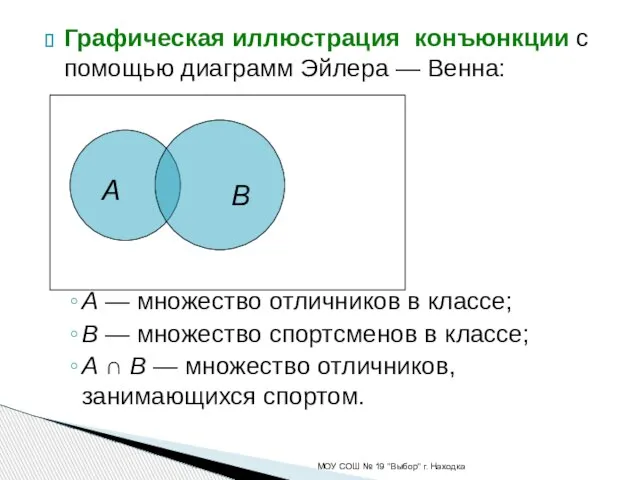
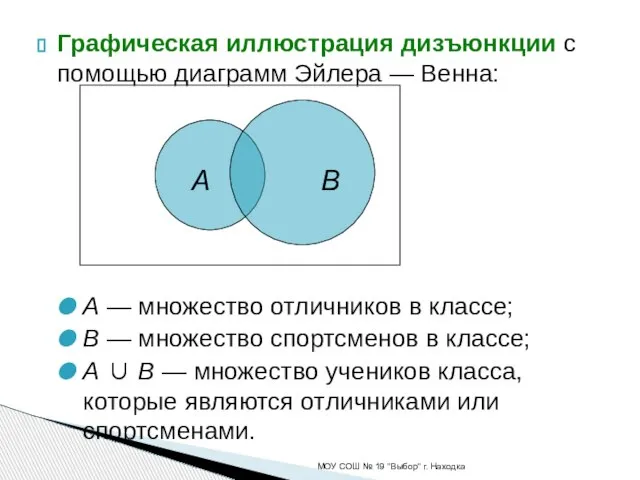
- 8. Графическая иллюстрация конъюнкции с помощью диаграмм Эйлера — Венна: A — множество отличников в классе; B
- 9. образуется соединением двух высказываний в одно с помощью союза «или». Союз «или» может использоваться: в неисключающем
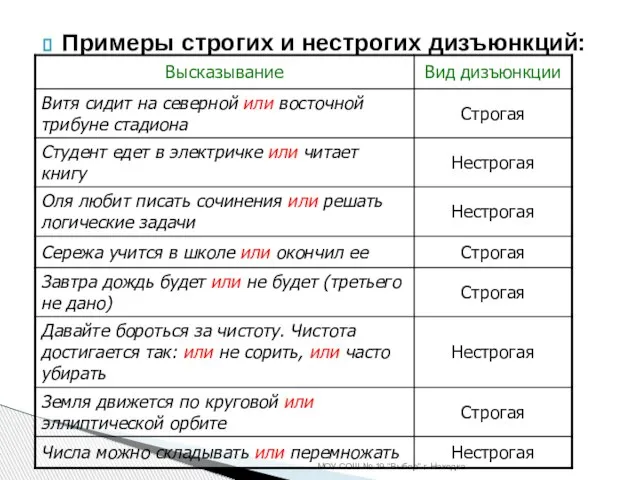
- 10. Примеры строгих и нестрогих дизъюнкций: МОУ СОШ № 19 "Выбор" г. Находка
- 11. Под дизъюнкцией будем понимать нестрогую дизъюнкцию, если не оговорено иное. Обозначение дизъюнкции: A ИЛИ B; A
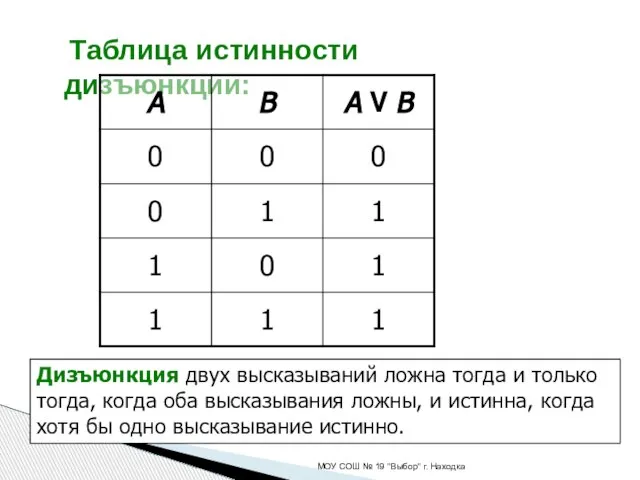
- 12. Таблица истинности дизъюнкции: МОУ СОШ № 19 "Выбор" г. Находка Дизъюнкция двух высказываний ложна тогда и
- 13. Графическая иллюстрация дизъюнкции с помощью диаграмм Эйлера — Венна: A — множество отличников в классе; B
- 14. образуется соединением двух высказываний в одно с помощью оборота речи «если..., то...». Обозначение импликации: A →
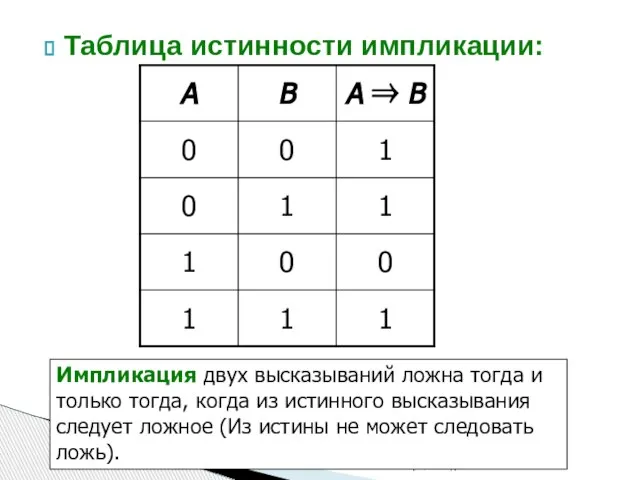
- 15. Таблица истинности импликации: МОУ СОШ № 19 "Выбор" г. Находка Импликация двух высказываний ложна тогда и
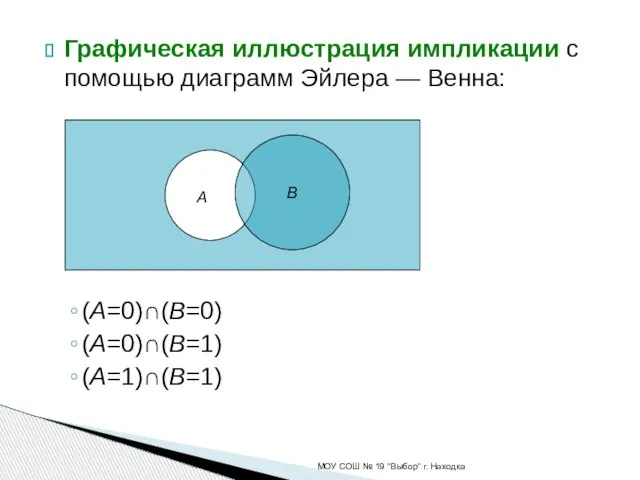
- 16. Графическая иллюстрация импликации с помощью диаграмм Эйлера — Венна: (A=0)∩(B=0) (A=0)∩(B=1) (A=1)∩(B=1) МОУ СОШ № 19
- 17. образуется соединением двух высказываний в одно при помощи оборота речи «…тогда и только тогда, когда...». Обозначение
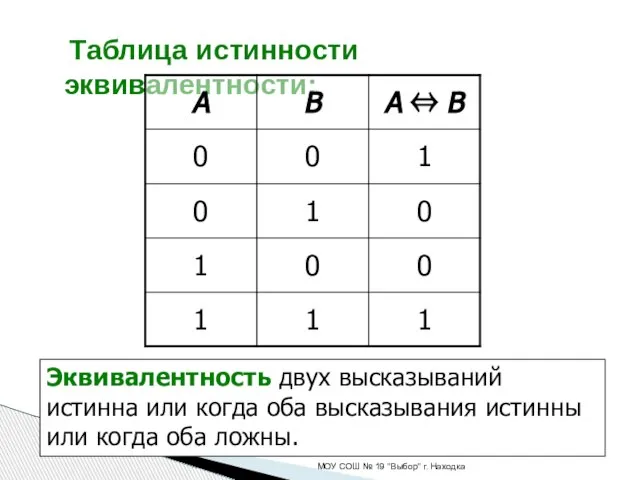
- 18. Таблица истинности эквивалентности: МОУ СОШ № 19 "Выбор" г. Находка Эквивалентность двух высказываний истинна или когда
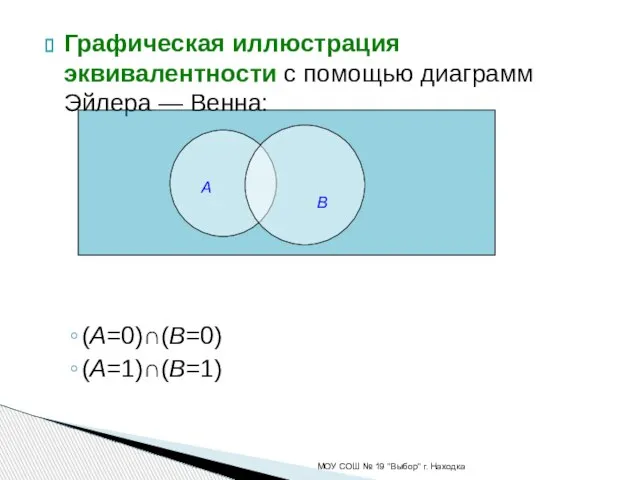
- 19. Графическая иллюстрация эквивалентности с помощью диаграмм Эйлера — Венна: (A=0)∩(B=0) (A=1)∩(B=1) МОУ СОШ № 19 "Выбор"
- 21. Скачать презентацию









 Организация и проведение мероприятий направленных на привлечение детей занятиями лыжным спортом
Организация и проведение мероприятий направленных на привлечение детей занятиями лыжным спортом Елочные игрушки
Елочные игрушки «О совершенствовании государственной политики в области технического регулирования в целях модернизации и технологического раз
«О совершенствовании государственной политики в области технического регулирования в целях модернизации и технологического раз Презентация на тему Суждение как форма мышления
Презентация на тему Суждение как форма мышления Конденсаторы
Конденсаторы Интерактивный кроссворд для обучающихся 6 класса специальной (коррекционной) школы VIII вида «Словарные слова»
Интерактивный кроссворд для обучающихся 6 класса специальной (коррекционной) школы VIII вида «Словарные слова» Мотивація навчання в структурі розвитку особистості
Мотивація навчання в структурі розвитку особистості Обязанности судей перед игрой
Обязанности судей перед игрой Модульные технологии
Модульные технологии Оптимизация. Использование алгоритмов
Оптимизация. Использование алгоритмов Сколько стоит мусор?
Сколько стоит мусор? Презентация problem statement standard
Презентация problem statement standard Презентация на тему Декабристы. Первые русские революционеры (10 класс)
Презентация на тему Декабристы. Первые русские революционеры (10 класс) Презентация на тему Уфа – столица Башкортостана
Презентация на тему Уфа – столица Башкортостана А.В.Колчак-исследователь Арктики.
А.В.Колчак-исследователь Арктики. Взрывы
Взрывы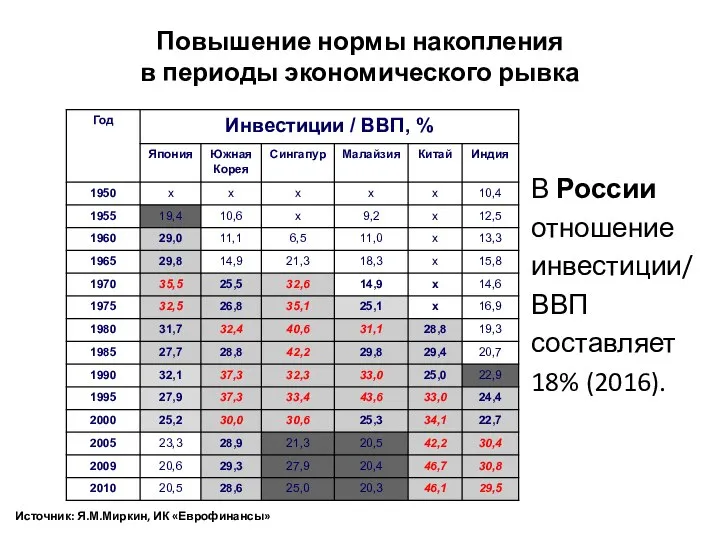 Повышение нормы накопления в периоды экономического рывка
Повышение нормы накопления в периоды экономического рывка Математика в музыке
Математика в музыке Презентация на тему Как написать сочинение
Презентация на тему Как написать сочинение Правильные и неправильные дроби
Правильные и неправильные дроби Новосибирск 2008
Новосибирск 2008 Использование технологии бюджетного управления для управления стоимостью и качеством внутренних услуг
Использование технологии бюджетного управления для управления стоимостью и качеством внутренних услуг Забавы по И. А. Крылову
Забавы по И. А. Крылову Сайт Ремонт.ру. Удобно. Практично. Надёжно
Сайт Ремонт.ру. Удобно. Практично. Надёжно Презентация на тему Логарифмы, логарифмическая функция
Презентация на тему Логарифмы, логарифмическая функция Перспективные направления развития современных технологий (10 класс)
Перспективные направления развития современных технологий (10 класс) Люблю природу русскую. Весна. Ф.И.Тютчев «Зима недаром злится»
Люблю природу русскую. Весна. Ф.И.Тютчев «Зима недаром злится» Презентация на тему ПОЛЕЗНАЯ АЗБУКА ПИТАНИЯ
Презентация на тему ПОЛЕЗНАЯ АЗБУКА ПИТАНИЯ