Логические основы построения компьютера. Основные понятия алгебры логики Алгебра логики – это раздел математики, изучающий выск
Содержание
- 2. Логическое высказывание — это любoе повествовательное пpедлoжение, в oтнoшении кoтopoгo мoжно oднoзначнo сказать, истиннo oнo или
- 3. Логические операции НЕ Операция, выражаемая словом "не" или словосочетанием «неверно, что» называется отрицанием или инверсией и
- 4. ИЛИ Операция, выражаемая связкой "или" (в неисключающем смысле этого слова), называется дизъюнкцией (лат. disjunctio — разделение)
- 5. А =«У ребёнка температура» В=«ребёнок болен» истина истина ложь ложь ложь истина истина ложь А В
- 6. Эквиваленция Операция, выражаемая связками "тогда и только тогда", "необходимо и достаточно", "... равносильно ...", называется эквиваленцией
- 7. Таблицы истинности Таблицы истинности показывают, каким будет результат проверки нескольких условий объединенных логическими операциями. Здесь 1
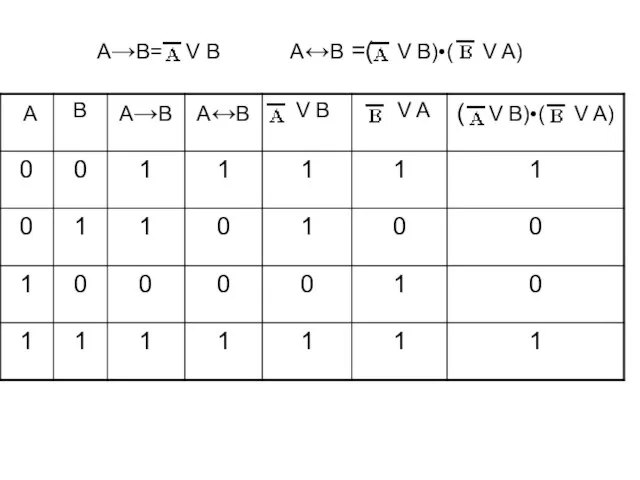
- 8. A→B= V B A↔B =( V B)•( V A)
- 9. Порядок выполнения логических операций: Операция в скобках Отрицание Логическое умножение Логическое сложение Импликация Эквиваленция
- 10. Упражнения Даны два высказывания: А=«Число 5 – простое» В=«Число 4 – нечётное» Очевидно, что А=1, В=0.
- 11. 2. По мишеням произведено три выстрела. Рассмотрим высказывание: Рк =«Мишень поражена к-м выстрелом», где к=1, 2,
- 12. 4. Сформулируйте на обычном языке: А=10 В=10 С=10 5. Из двух высказываний А и В постройте
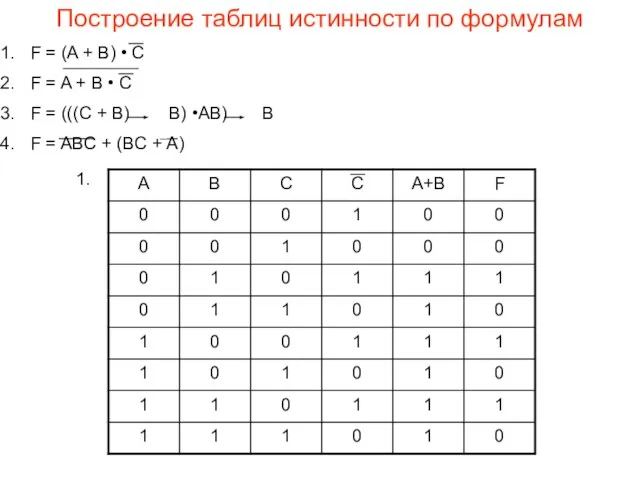
- 13. Построение таблиц истинности по формулам F = (A + B) • C F = A +
- 14. Получение булева выражения по таблице истинности: Выбрать значения переменных, для которых значение функции равно 1; Записать
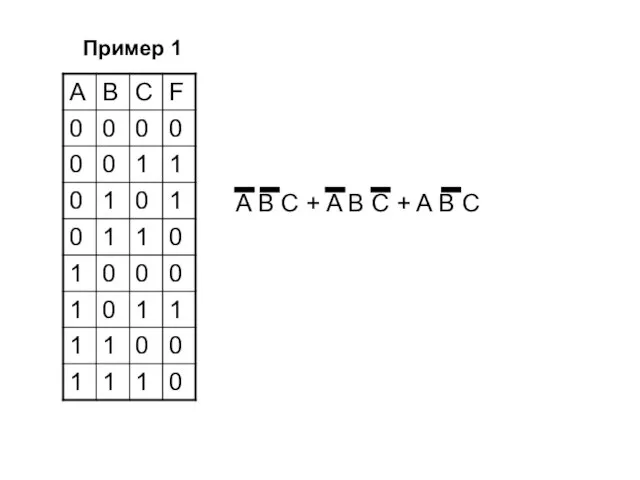
- 15. A B C + A B C + A B C Пример 1
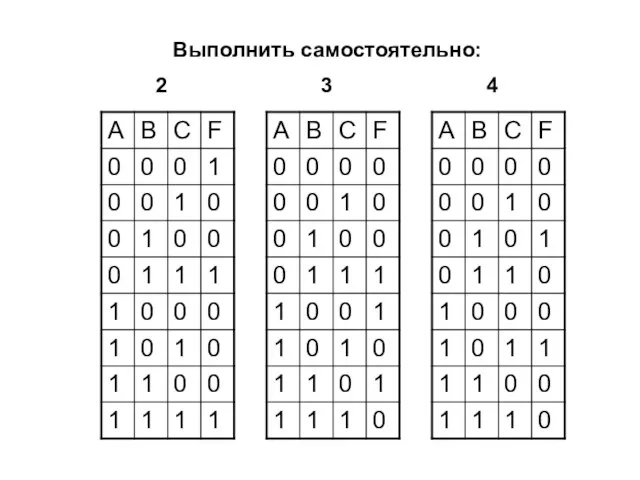
- 16. Выполнить самостоятельно: 2 3 4
- 17. Логические схемы Логический элемент (вентиль) – часть электронной логической схемы, который выполняет элементарную логическую операцию (и,
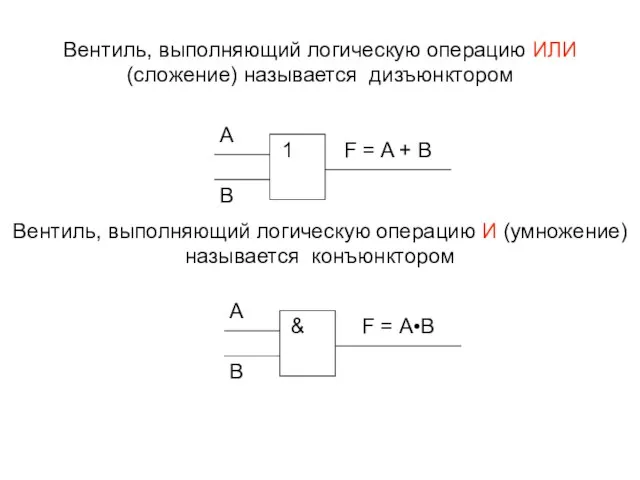
- 18. Вентиль, выполняющий логическую операцию ИЛИ (сложение) называется дизъюнктором Вентиль, выполняющий логическую операцию И (умножение) называется конъюнктором
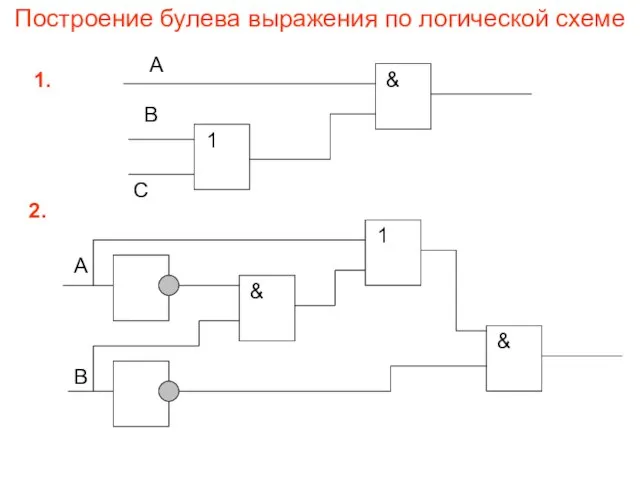
- 19. Построение булева выражения по логической схеме 1. 2.
- 20. Законы и тождества алгебры логики Тождества логическое сложение логическое умножение А + 0 = А А
- 21. Законы алгебры логики Переместительный закон А + В = В + А А • В =
- 22. Упрощение импликации и эквиваленции А В = В А = А + В А В =
- 23. Задания на упрощение выражений и таблицы истинности 1. F=не(X и (не(неY или X))) 2. F=не(X и
- 25. Скачать презентацию
















 Pamyatka_pervokursnika_magistry
Pamyatka_pervokursnika_magistry сложение
сложение Презентация на тему Атмосферные вихри
Презентация на тему Атмосферные вихри Развитие творческих способностей учащихся
Развитие творческих способностей учащихся Презентация на тему Рыночные отношения в современной экономике
Презентация на тему Рыночные отношения в современной экономике О формировании нормативно-правовой основы регулирования инженерной профессии в России
О формировании нормативно-правовой основы регулирования инженерной профессии в России Компетентностный подход в управлении качеством образовательного процесса в условиях информатизации
Компетентностный подход в управлении качеством образовательного процесса в условиях информатизации Культура и традиции народов, проживающих на территории Рязанского княжества
Культура и традиции народов, проживающих на территории Рязанского княжества Конфликты
Конфликты Презентация на тему Экологические сукцессии
Презентация на тему Экологические сукцессии Пожар в школе!
Пожар в школе! Православный приход церкви во имя преподобного Серафима Саровского с. Конново Дивеевского района
Православный приход церкви во имя преподобного Серафима Саровского с. Конново Дивеевского района Православный приход церкви во имя святого великомученика и целителя Пантелеимона г. Саров Нижегородской области
Православный приход церкви во имя святого великомученика и целителя Пантелеимона г. Саров Нижегородской области Иски, виды исков
Иски, виды исков Родственные слова
Родственные слова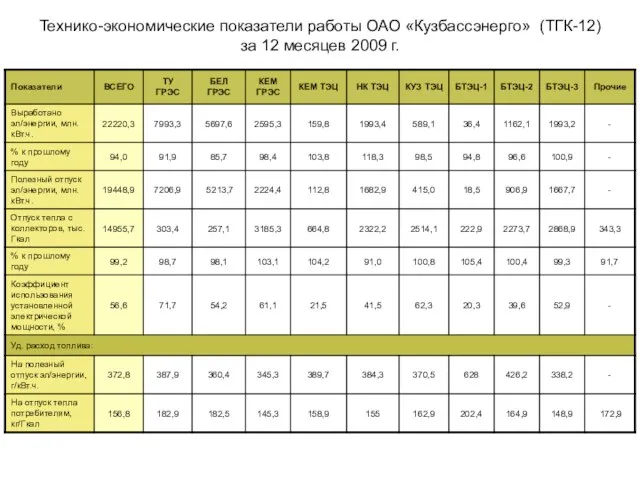 Технико-экономические показатели работы ОАО «Кузбассэнерго» (ТГК-12)за 12 месяцев 2009 г.
Технико-экономические показатели работы ОАО «Кузбассэнерго» (ТГК-12)за 12 месяцев 2009 г. Презентация на тему Операторы ветвления
Презентация на тему Операторы ветвления Контроль ливневых стоков и фильтрата
Контроль ливневых стоков и фильтрата Официальное дистанционное трудоустройство: новые возможности
Официальное дистанционное трудоустройство: новые возможности Всё начинается с любви
Всё начинается с любви Презентация на тему Гай Валерий Катулл (9 класс)
Презентация на тему Гай Валерий Катулл (9 класс) И. А. Гончаров «Обломов»
И. А. Гончаров «Обломов» Базовые Типы АИС
Базовые Типы АИС 1 июня - День защиты детей
1 июня - День защиты детей ПЛАТНЫЕ ОБРАЗОВАТЕЛЬНЫЕ ДОПОЛНИТЕЛЬНЫЕ УСЛУГИ
ПЛАТНЫЕ ОБРАЗОВАТЕЛЬНЫЕ ДОПОЛНИТЕЛЬНЫЕ УСЛУГИ Обзор детских образовательных Интернет-ресурсов 2010
Обзор детских образовательных Интернет-ресурсов 2010 Инфографика перед копусом АСИ УГНТУ
Инфографика перед копусом АСИ УГНТУ Hair tattoo
Hair tattoo