Мастер -класс "Использование презентаций Power Point на урока математики при построении графиков функции"
Содержание
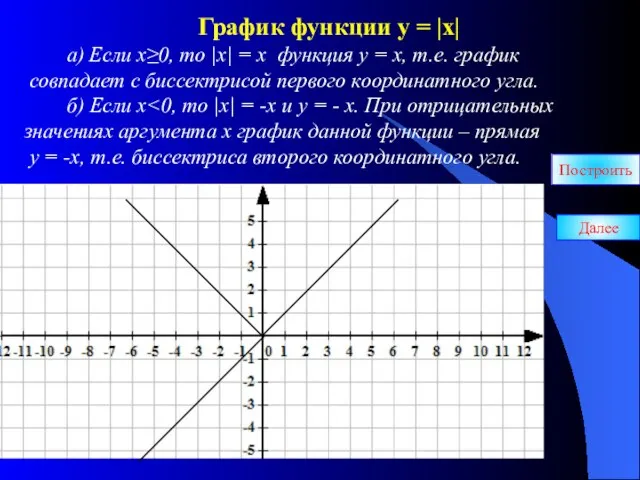
- 2. График функции у = |х| а) Если х≥0, то |х| = х функция у = х,
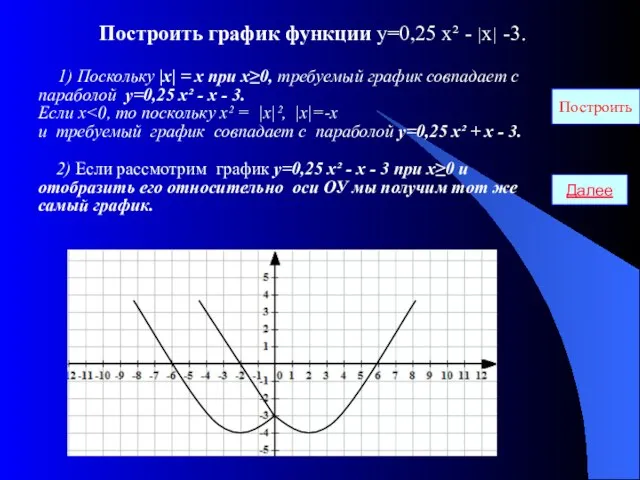
- 3. Построить график функции у=0,25 х² - |х| -3. 1) Поскольку |х| = х при х≥0, требуемый
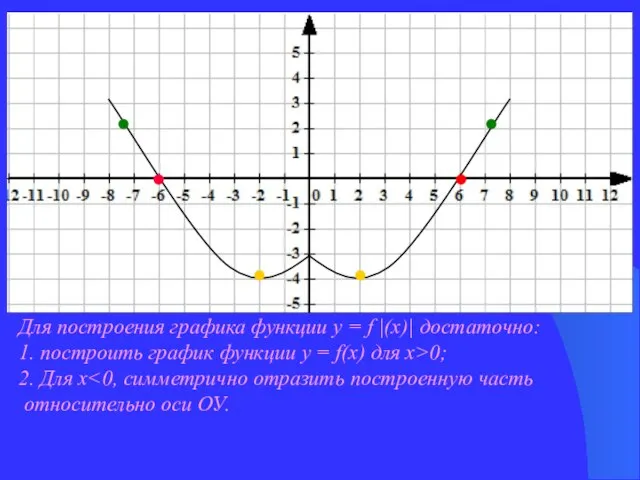
- 4. Для построения графика функции у = f |(х)| достаточно: 1. построить график функции у = f(х)
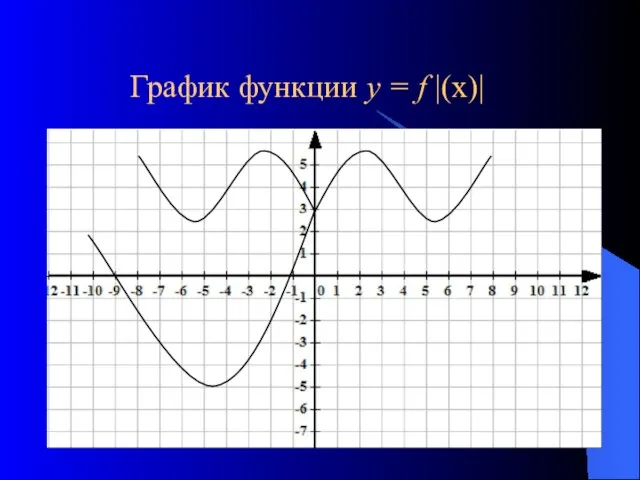
- 5. График функции у = f |(х)|
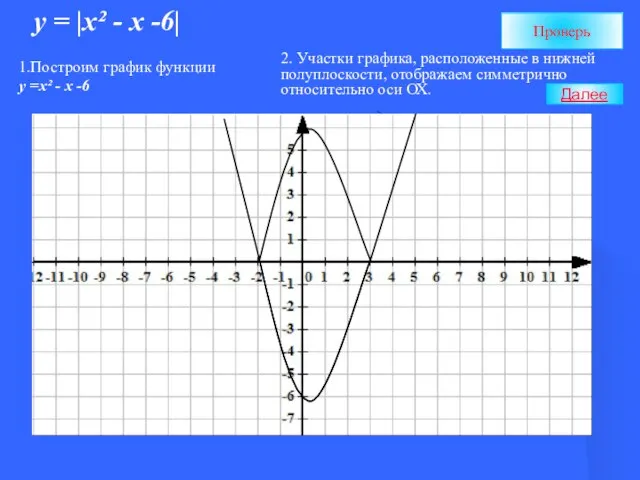
- 6. у = |х² - х -6| Проверь 1.Построим график функции у =х² - х -6 2.
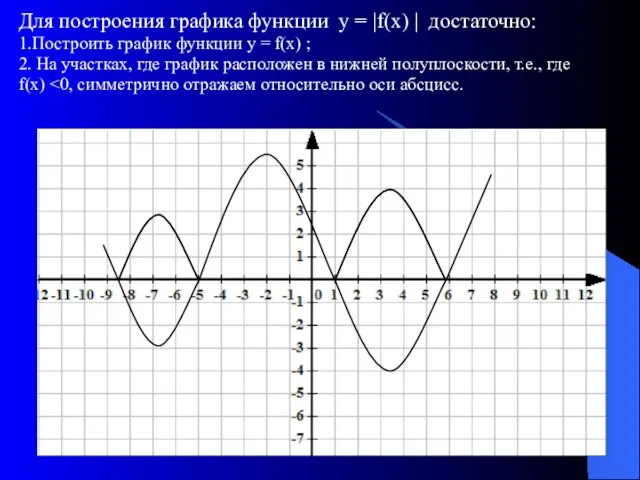
- 7. Для построения графика функции у = |f(х) | достаточно: 1.Построить график функции у = f(х) ;
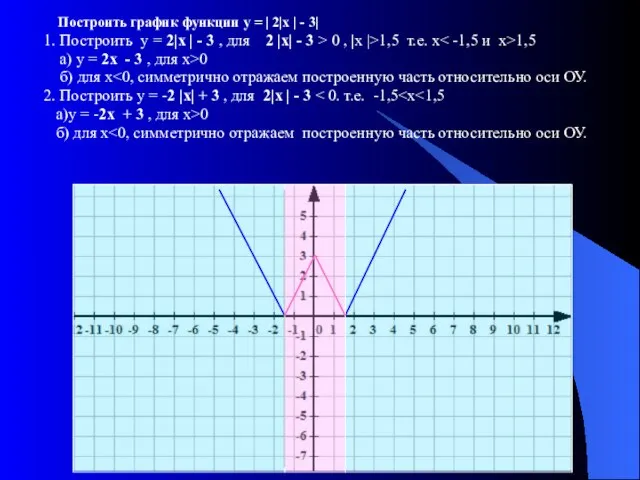
- 8. Построить график функции у = | 2|х | - 3| 1. Построить у = 2|х |
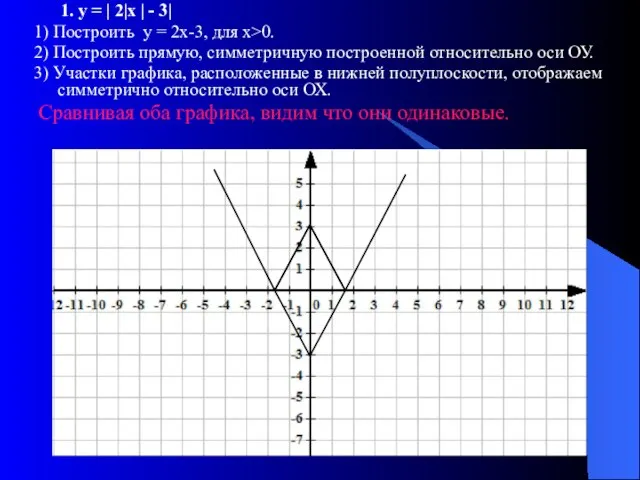
- 9. 1. у = | 2|х | - 3| 1) Построить у = 2х-3, для х>0. 2)
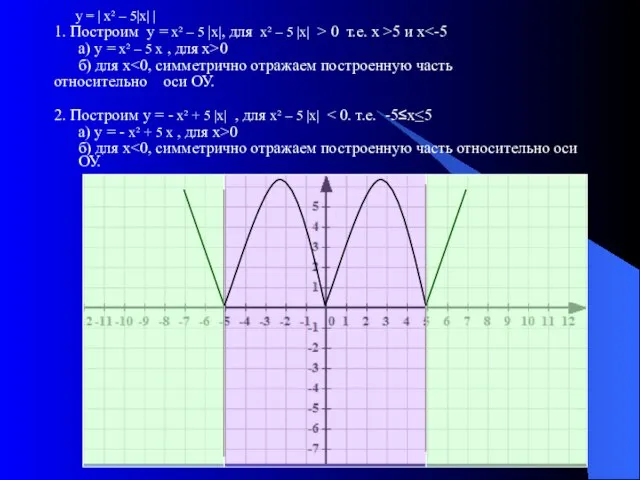
- 10. у = | х² – 5|х| | 1. Построим у = х² – 5 |х|, для
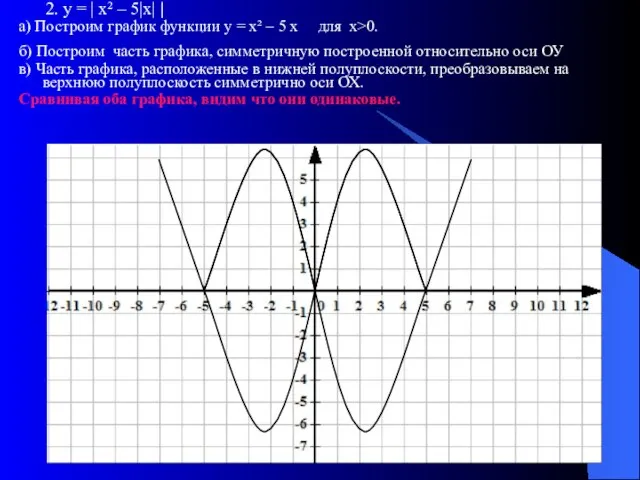
- 11. 2. у = | х² – 5|х| | а) Построим график функции у = х² –
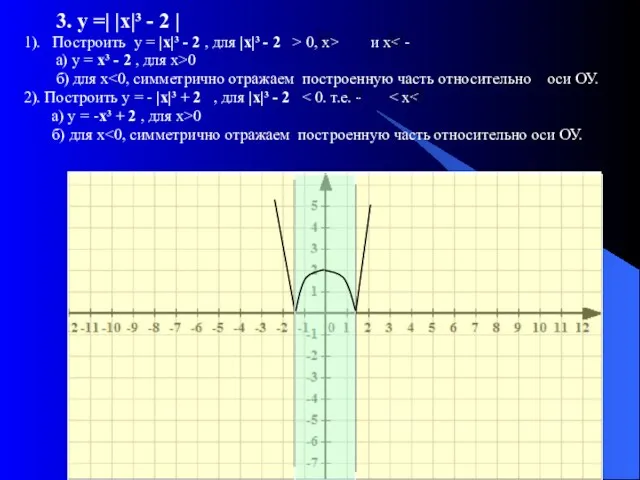
- 12. 3. у =| |х|³ - 2 | 1). Построить у = |х|³ - 2 , для
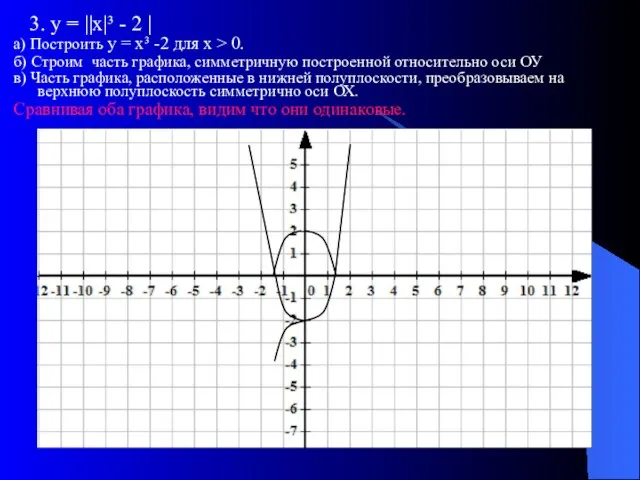
- 13. 3. у = ||х|³ - 2 | а) Построить у = х³ -2 для х >
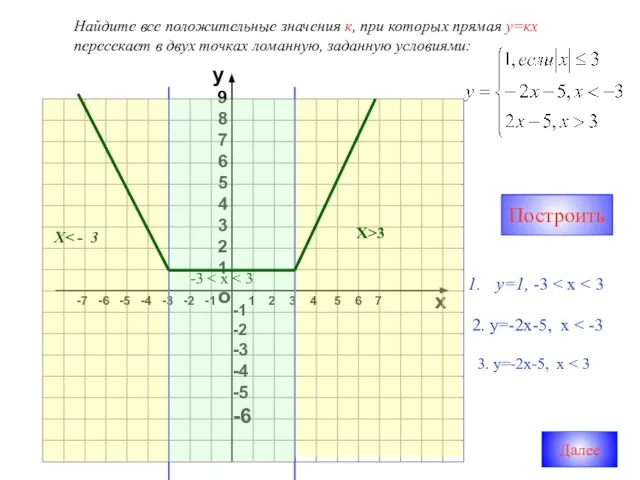
- 14. Найдите все положительные значения к, при которых прямая у=кх пересекает в двух точках ломанную, заданную условиями:
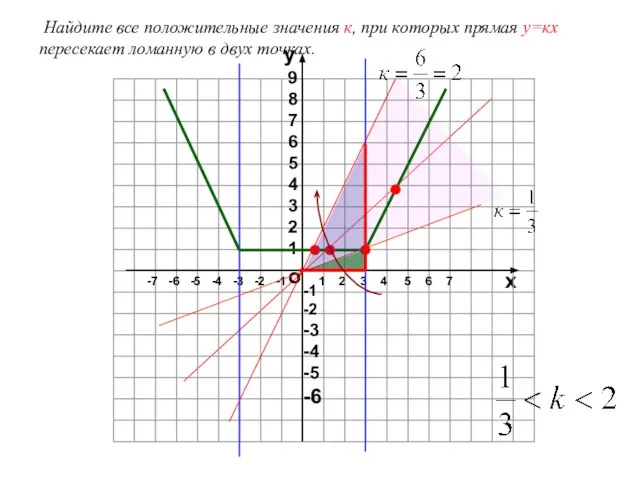
- 15. Найдите все положительные значения к, при которых прямая у=кх пересекает ломанную в двух точках.
- 17. Скачать презентацию
 Пермский край: инвестиционные возможности
Пермский край: инвестиционные возможности Системные платы Gigabyte
Системные платы Gigabyte Кроссворд на английском языке
Кроссворд на английском языке Проектирование системы электроснабжения электроаппаратного завода
Проектирование системы электроснабжения электроаппаратного завода Древние образы народного искусства
Древние образы народного искусства Решение квадратных уравнений
Решение квадратных уравнений Антимонопольное регулирование в авторитейле
Антимонопольное регулирование в авторитейле Завтрак чемпиона от Широковой Полины. Омлет с сыром, молоко
Завтрак чемпиона от Широковой Полины. Омлет с сыром, молоко Highlights of sports
Highlights of sports Просвещенный абсолютизм в России
Просвещенный абсолютизм в России Феофан Грек, Андрей Рублев
Феофан Грек, Андрей Рублев "Платон" - Философия
"Платон" - Философия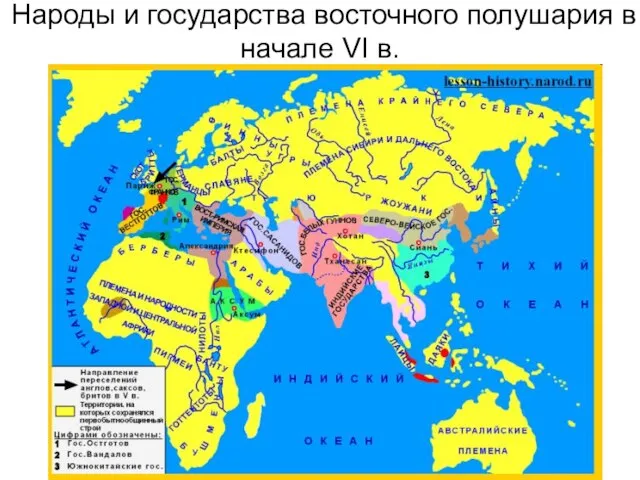 Народы и государства восточного полушария в начале VI в.
Народы и государства восточного полушария в начале VI в. Деятельность
Деятельность ЖИЗНЬ КЛАССА 1 сентября Посвящение в гимназисты Хореография Экскурсия в Автогородок Новогодний калейдоскоп Масленица Наша пл
ЖИЗНЬ КЛАССА 1 сентября Посвящение в гимназисты Хореография Экскурсия в Автогородок Новогодний калейдоскоп Масленица Наша пл ОРГАНИЗАЦИЯ ПЕРЕВОЗКИ ВНЕШНЕТОРГОВЫХ ГРУЗОВ АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ Преподаватель: доцент кафедры МЭО, к.э.н., Журова А.В.
ОРГАНИЗАЦИЯ ПЕРЕВОЗКИ ВНЕШНЕТОРГОВЫХ ГРУЗОВ АВТОМОБИЛЬНЫМ ТРАНСПОРТОМ Преподаватель: доцент кафедры МЭО, к.э.н., Журова А.В. Участники "Первого Дома на Родине" отмечают свою первую Хануку в Израиле
Участники "Первого Дома на Родине" отмечают свою первую Хануку в Израиле Реклама и маркетинг
Реклама и маркетинг Изображение цветка пиона в разных техниках художественной обработки
Изображение цветка пиона в разных техниках художественной обработки Мутационная изменчивость 10 класс
Мутационная изменчивость 10 класс Byredo Blanche. Парфюмерия
Byredo Blanche. Парфюмерия Элетромеханический замок с убегающим кодом
Элетромеханический замок с убегающим кодом Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут
Особенности формирования требований информационной безопасности Реестра источников ионизирующего излучения (ИИИ), которые могут Valentine game
Valentine game Аспартам
Аспартам Попечительский совет или Управляющий совет?
Попечительский совет или Управляющий совет? Компания Декорсталь – Производитель декоративных сталей
Компания Декорсталь – Производитель декоративных сталей Taller de comunicación oral y escrita
Taller de comunicación oral y escrita