Содержание
- 2. ax2+ bx + c =0 D = b2 – 4ac Если D D = 0, то
- 3. b = 2k (четное число) D1= Если D 0, то x =
- 4. Неполные квадратные уравнения:
- 5. Теорема Виета x1 и х2 – корни уравнения x1 и х2 – корни уравнения
- 6. Установите связь между квадратным уравнением и способами его решения ax2+ bx + c =0 ax2+ 2kx
- 7. Какое уравнение «лишнее» (1) (2) (3) (4)
- 8. 1) Один из корней квадратного уравнения равен - 3. Найдите коэффициент k и второй корень 2)
- 9. Решить уравнения
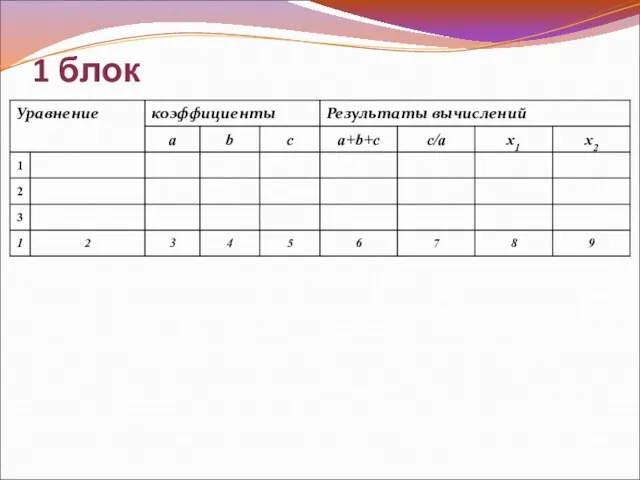
- 10. 1 блок
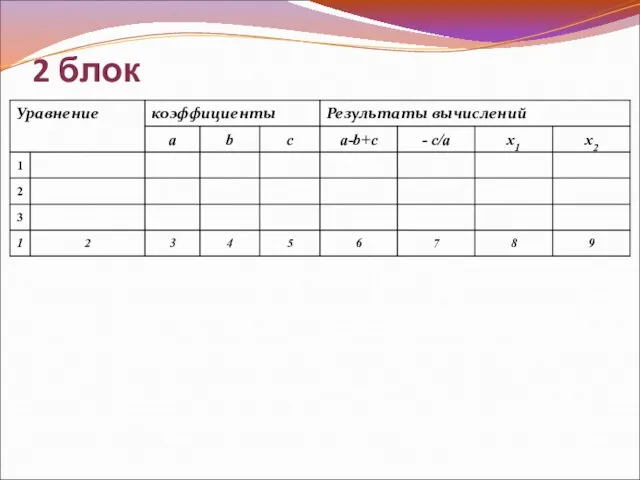
- 11. 2 блок
- 12. Выводы 1. aх2+bx+c=0, a+b+c=0 => x1=1, x2= с/а 2. aх2+bx+c=0, a-b+c=0 => x1=-1, x2= -с/а 3.
- 14. Скачать презентацию









 Класс Млекопитающие
Класс Млекопитающие Особенности костюма жителей Дона» (на материале романа М. А. Шолохова «Тихий Дон»)
Особенности костюма жителей Дона» (на материале романа М. А. Шолохова «Тихий Дон») Несуществующие животные
Несуществующие животные Презентация на тему: Морской бой
Презентация на тему: Морской бой Презентация на тему Архитектура 18 века в России
Презентация на тему Архитектура 18 века в России Презентация на тему Климат Северной Америки
Презентация на тему Климат Северной Америки Бонус ВР
Бонус ВР Теория государства и права
Теория государства и права Постэмбриональное развитие
Постэмбриональное развитие Декларация прав и свобод человека и гражданина от 22 ноября 1991 года
Декларация прав и свобод человека и гражданина от 22 ноября 1991 года Построение системы внутрикорпоративного обучения
Построение системы внутрикорпоративного обучения Литературное развитие
Литературное развитие МОУ Плоскошская СОШ
МОУ Плоскошская СОШ Современные способы предоставления метеорологической информации в Северо-Западном филиале . Директор СЗФ ФГБУ «Авиаметтелек
Современные способы предоставления метеорологической информации в Северо-Западном филиале . Директор СЗФ ФГБУ «Авиаметтелек Сказки на английском
Сказки на английском Презентация на тему История Санкт-Петербурга
Презентация на тему История Санкт-Петербурга  Формы ДНК
Формы ДНК Моя мама!
Моя мама! Послание Президента России Дмитрия Анатольевича Медведева к Федеральному собранию от 12 ноября 2009 г
Послание Президента России Дмитрия Анатольевича Медведева к Федеральному собранию от 12 ноября 2009 г Стан електронів у атомі
Стан електронів у атомі Структура энергетики РФ
Структура энергетики РФ Я здоровье берегу - космонавтом стать хочу
Я здоровье берегу - космонавтом стать хочу Презентация на тему Образ жизни наших предков (3 класс)
Презентация на тему Образ жизни наших предков (3 класс) Масленица (1-8 класс)
Масленица (1-8 класс) Апрель
Апрель Электронные таблицы. Термины и понятия
Электронные таблицы. Термины и понятия Всероссийский конкурс Большая перемена
Всероссийский конкурс Большая перемена Проектирование однотабличной БД
Проектирование однотабличной БД