Содержание
- 2. Генеральной совокупностью называют совокупность всех объектов, над которыми производят наблюдение. Выборочной совокупностью (выборкой) называют часть отобранных
- 3. Способы отбора 1. Отбор, не требующий расчленения генеральной совокупности на части: а) простой случайный бесповторный отбор,
- 4. Наблюдаемые значения xi называют вариантами. Последовательность вариант, записанных в возра-стающем порядке называют вариационным рядом. Частотой варианты
- 6. Полигоном частот называют ломаную, отрезки которой последовательно соединяют точки (xi, ni). Полигоном относительных частот называют ломаную,
- 7. Функция распределения случайной величины Х: F(x) = p(X Теоретической функцией распределения называют функцию распределения генеральной совокупности.
- 8. Выборочная характеристика (*) используемая для нахождения приближённого значения неизвестной генеральной характеристики , называет-ся её точечной статистической
- 9. Выборочная средняя: 2. Если ui = hxi для всех i, где h – некоторое число, то
- 10. Выборочная дисперсия: 2. Если ui = hxi для всех i, где h – некоторое число, то
- 11. Исправленная выборочная дисперсия: Выборочное среднее квадратическое отклонение: Исправленное выборочное среднее квадратическое отклонение:
- 12. 1-ая группа: N1 элементов 2-ая группа: N2 элементов j-тая группа: Nj элементов … … – групповые
- 13. Метод максимального (наибольшего) правдоподобия x1, x2, … , xn – выборка
- 14. I. Дискретное распределение p(x1), … , p(xn) – вероятности значений x1, … , xn Пример. Распределение
- 15. Алгоритм исследования на максимум функции правдоподобия 1. 3. 2. 4.
- 16. Метод моментов I. Оценка одного параметра Пример. Показательное распределение II. Оценка двух параметров Пример. Нормальное распределение
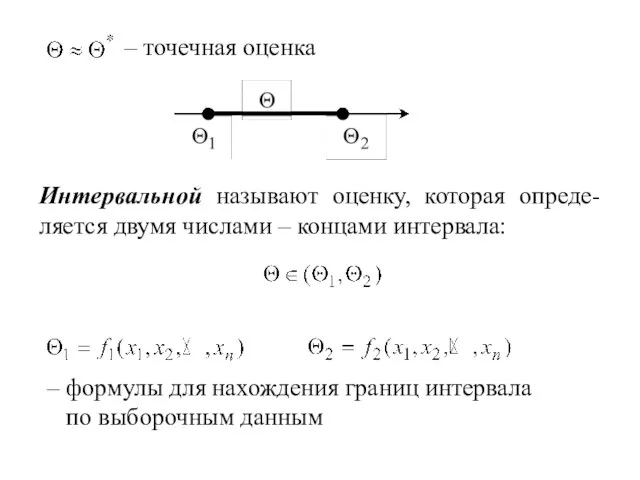
- 17. – точечная оценка Интервальной называют оценку, которая опреде-ляется двумя числами – концами интервала: – формулы для
- 19. 1. Пусть Х – непрерывная случайная величина, F(x) – функция распределения, f(x) – плотность распределения (*)
- 20. Алгоритм нахождения доверительных интервалов или Вопрос: какой вид имеют функции F(x) и f(x) ?
- 21. Пусть генеральная совокупность имеет нормальное распределение
- 22. или Шаг 2.
- 24. Пусть генеральная совокупность имеет нормальное распределение
- 25. Шаг 2.
- 27. Пусть генеральная совокупность имеет нормальное распределение 2. Находим точечную оценку: .
- 28. Шаг 2.
- 29. Доверительным интервалом является интервал:
- 30. Шаг 2. Способ 2. Доверительным интервалом является интервал:
- 31. Пусть производятся независимые испытания с неиз-вестной вероятностью р появления события А в каждом испытании. р –
- 32. – случайная величина, имеющая нормальное распределение с нулевым математическим ожиданием и единичной дисперсией или
- 33. Шаг 2. Доверительным интервалом является интервал: (р1, р2)
- 34. При больших значениях n (порядка сотен) и Доверительным интервалом является интервал:
- 36. Скачать презентацию



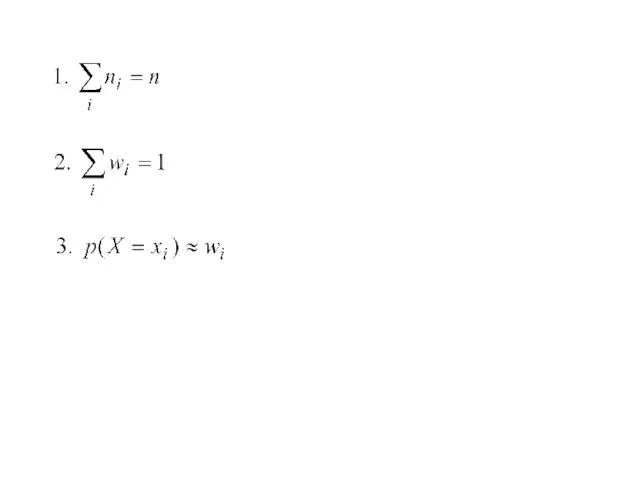




























 Международный Юридический институт приглашает всех желающих на День Открытых дверей!
Международный Юридический институт приглашает всех желающих на День Открытых дверей! «Ожившие страницы русской истории в картинах художника Василия Сурикова»
«Ожившие страницы русской истории в картинах художника Василия Сурикова» Теоретические основы налогообложения
Теоретические основы налогообложения Отделение современной гитары. Школа МЭШДОМ, г. Калуга
Отделение современной гитары. Школа МЭШДОМ, г. Калуга Фотокросс Добру откроются сердца
Фотокросс Добру откроются сердца Современные методы и средства производства СТЭ. Лекция 1. Методология производства СТЭ
Современные методы и средства производства СТЭ. Лекция 1. Методология производства СТЭ Кадровая политика. Основные термины
Кадровая политика. Основные термины Строение и работа мышц
Строение и работа мышц Presentation Title Here Subtitle
Presentation Title Here Subtitle  Как животные защищаются
Как животные защищаются Способы вальцовки и развальцовки труб
Способы вальцовки и развальцовки труб Happy Birthday Chevrolet!!!
Happy Birthday Chevrolet!!! Intel. Історія успіху
Intel. Історія успіху студсовет
студсовет Презентация на тему Профилактика ОРВИ гриппа
Презентация на тему Профилактика ОРВИ гриппа XXVI-ая Межвузовская научнопрактическая конференция молодых ученых и студентов г. Волжского
XXVI-ая Межвузовская научнопрактическая конференция молодых ученых и студентов г. Волжского Что учитывать при перепланировке
Что учитывать при перепланировке Анализ работы кафедры общественных и гуманитарных наукза 2010 – 2011 учебный год
Анализ работы кафедры общественных и гуманитарных наукза 2010 – 2011 учебный год Презентация на тему КОНСТАНТИН ГЕОРГИЕВИЧ ПАУСТОВСКИЙ
Презентация на тему КОНСТАНТИН ГЕОРГИЕВИЧ ПАУСТОВСКИЙ  Элективные курсы для предпрофильной подготовки учащихся 9-го класса по математике
Элективные курсы для предпрофильной подготовки учащихся 9-го класса по математике Золотая осень. Рисунок осеннего дерева с натуры и по памяти
Золотая осень. Рисунок осеннего дерева с натуры и по памяти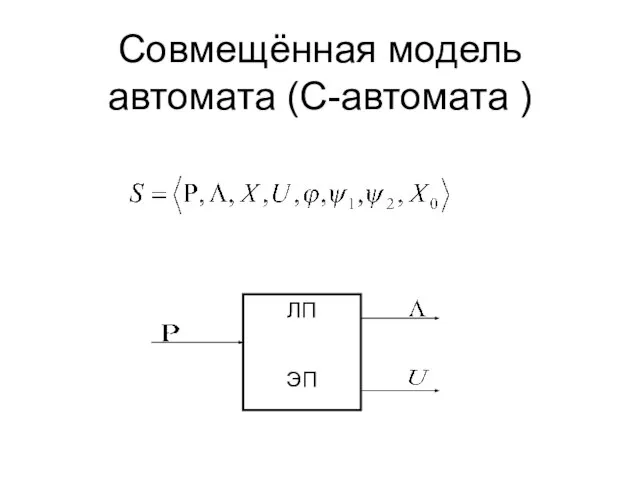 Структурный синтез C-автомата
Структурный синтез C-автомата Программное создание web-фрагментов, ускорителей и средств визуального поиска
Программное создание web-фрагментов, ускорителей и средств визуального поиска МОУ «Ракитянская средняя общеобразовательная школа № 2»
МОУ «Ракитянская средняя общеобразовательная школа № 2» Диаграммы
Диаграммы Շառլ Ազնավուր
Շառլ Ազնավուր Лигнвистическая сказка как средство преодоления трудностей при изучении морфологии русского языка
Лигнвистическая сказка как средство преодоления трудностей при изучении морфологии русского языка Возникновение института праздного класса
Возникновение института праздного класса