Математические методы в психологии. Корреляционный анализ

Коэффициент корреляции – двумерная описательная статистика, количественная мера взаимосвязи (совместной изменчивости) двух переменных.

История разработки и применения кк для исследования взаимосвязей фактически началась одновременно с возникновением измерительного подхода к исследованию индивидуальных различий – в 1870-1880 гг.

Пионером в измерении способностей человека, как и автором самого термина «коэффициент корреляции», был Френсиз Гальтон, а самые популярные кк были разработаны его последователем Карлом Пирсоном.

3 важных для психологии КК:
r- Пирсона;
r-Спирмена;
t-Кендалла (тау).
Их общая особенность: отражение взаимосвязи 2-х признаков, измеренных в количественной шкале – ранговой или метрической.

Любое исследование можно свести к изучению корреляций. Но! Можно различить 2 класса задач:
Исследование корреляций – 2 переменные представлены в числовой шкале;
Исследование различий – хотя бы одна из 2 переменных представлена в номинативной шкале.

Понятие корреляции
Взаимосвязи на языке математики обычно описываются при помощи функций.

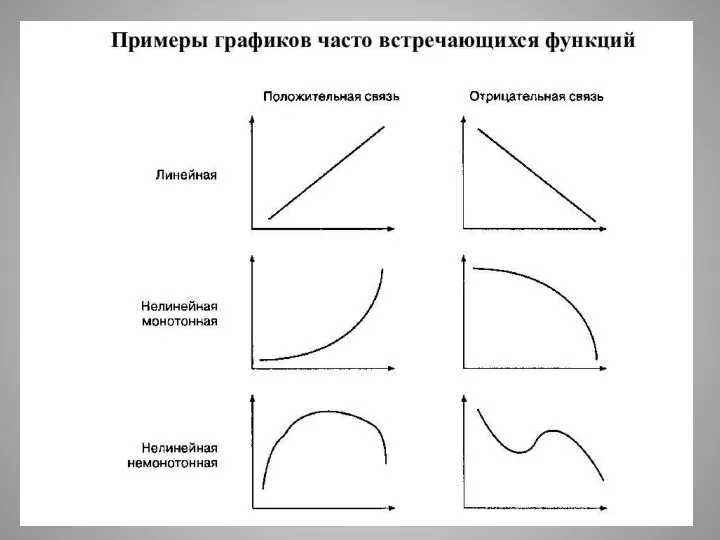
Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, то функция является линейной.
Любая другая – нелинейной.

Если увеличение одной переменной связано с увеличением другой, то связь – положительная (прямая); если увеличение одной переменной связано с уменьшением другой, то связь - отрицательная (обратная).

Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция – монотонная; в противном случае функцию называют немонотонной.

Важно!
Даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная (стохастическая): одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот).

Функциональная связь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков.

Наглядное представление о характере вероятностной связи дает диаграмма рассеивания –график, оси которого соответствуют значениям двух переменных, в каждой испытуемый представляет собой точку.

Коэффициент корреляции
Это количественная мера силы и направления вероятностной взаимосвязи двух переменных; принимает значение в диапазоне от – 1 до +1.

Сила связи достигает максимума при условии взаимно однозначного соответствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот), эмпирическая взаимосвязь при этом совпадает с функциональной линейной связью.

Показателем силы связи является абсолютная (без учета знака) величина коэффициента корреляции.