Содержание
- 2. Цель моей работы - доказать, что софизмы являются не просто интеллектуальным мошенничеством, а важным двигателем человеческой
- 3. Введение. Мозги обязаны трудиться Софизмами принято называть утверждения, в доказательствах которых кроются незаметные, а подчас и
- 4. ПОНЯТИЕ «СОФИЗМ» Софизм – (от греческого sophisma , «мастерство, умение, хитрая выдумка, уловка») - умозаключение или
- 5. ЭКСКУРС В ИСТОРИЮ Софистами называли группу древнегреческих философов 4-5 века до н.э., достигших большого искусства в
- 6. АРИФМЕТИЧЕСКИЕ СОФИЗМЫ Арифметика - (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь
- 7. 2. «Число, равное другому числу, одновременно и больше, и меньше его». Возьмем два произвольных положительных равных
- 8. 3. «2+2=5» Чтобы доказать, что 2+2=5, можно всего лишь доказать, что 4=5 Начнём с равенства: 16-36=25-45
- 9. 4.«Дважды два равно пяти» Обозначим 4=а, 5=b, (a+b)/2=d. Имеем: a+b=2d, a=2d-b, 2d-a=b. перемножим два последних равенства
- 10. 5. «Пропавший рубль» Три подруги зашли в кафе выпить по чашке кофе. Выпили. Официант принес им
- 11. АЛГЕБРАИЧЕСКИЕ СОФИЗМЫ Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к
- 12. 1. «Два неодинаковых натуральных числа равны между собой» Решим систему двух уравнений: х+2у=6, (1) у=4- х/2
- 13. 2. «Отрицательное число больше положительного». Возьмем два положительных числа а и с. Сравним два отношения: а/-c
- 14. 3.Любое число a равно меньшему числу b Начнём с равенства: a=b+c Умножим обе его части на
- 15. 4.Уравнение x-a=0 не имеет корней Дано уравнение: x-a=0 Разделим всё на x-a, получим: 1=0 Это равенство
- 16. 5.Вес слона равен весу комара. Пусть х – вес слона, а у – вес комара. Обозначим
- 17. ГЕОМЕТРИЧЕСКИЕ СОФИЗМЫ Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или парадоксальное
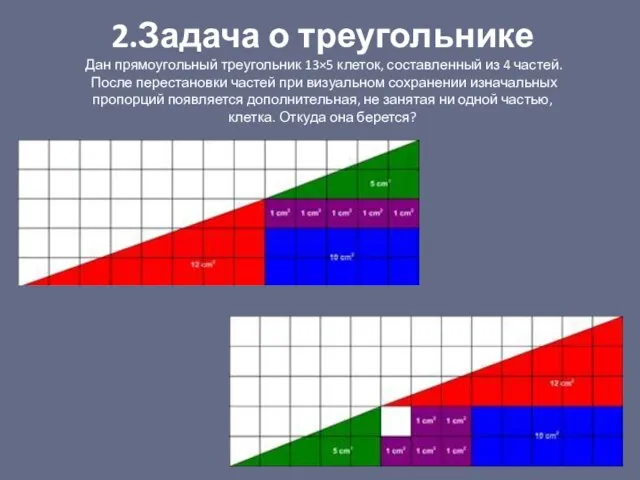
- 18. 2.Задача о треугольнике Дан прямоугольный треугольник 13×5 клеток, составленный из 4 частей. После перестановки частей при
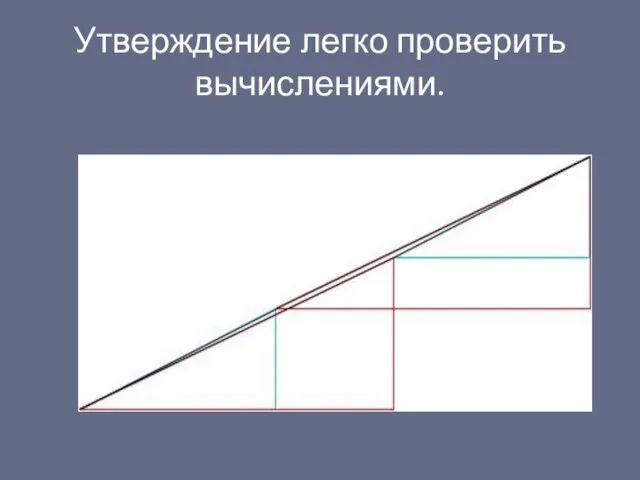
- 19. Утверждение легко проверить вычислениями.
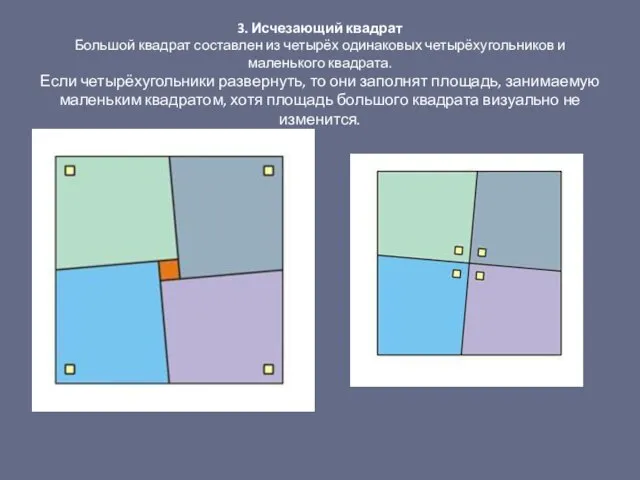
- 20. 3. Исчезающий квадрат Большой квадрат составлен из четырёх одинаковых четырёхугольников и маленького квадрата. Если четырёхугольники развернуть,
- 21. Софизм Аристотеля Все окружности имеют одинаковую длину. Ведь при оборачивании двух окружностей с разными диаметрами ОА1
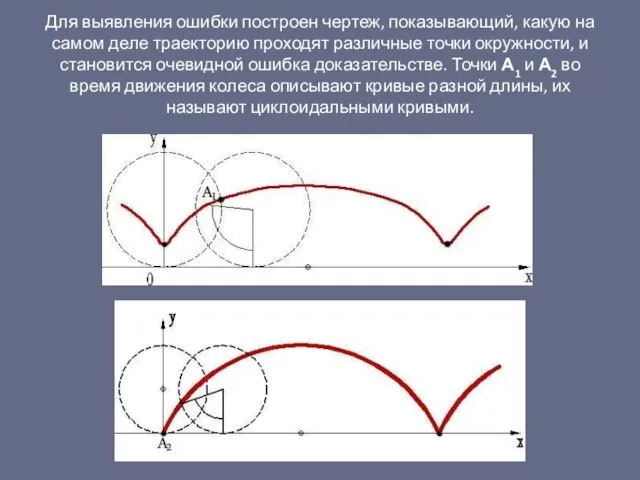
- 22. Для выявления ошибки построен чертеж, показывающий, какую на самом деле траекторию проходят различные точки окружности, и
- 23. ПРОЧИЕ СОФИЗМЫ Кроме математических софизмов, существует множество других, например: логические, терминологические, психологические и т.д. Понять абсурдность
- 24. «Самое быстрое существо не способно догнать самое медленное» Быстроногий Ахиллес никогда не настигнет медлительную черепаху. Пока
- 25. «Куча» Одна песчинка не есть куча песка. Если n песчинок не есть куча песка, то и
- 26. «Софизм Эватла» Эватл брал уроки софистики у софиста Протагора под тем условием, что гонорар он уплатит
- 27. Заключение. О математических софизмах можно говорить бесконечно много, как и о математике в целом. Изо дня
- 29. Скачать презентацию






















 и формирование отчетности
и формирование отчетности Презентация на тему Швейные товары
Презентация на тему Швейные товары  Филологи
Филологи АУДИТ
АУДИТ Проектирование СКС коттеджного участка из бруса
Проектирование СКС коттеджного участка из бруса Интеграция риск-менеджмента в ключевые процессы принятия решений
Интеграция риск-менеджмента в ключевые процессы принятия решений Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке
Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке Выполненное и планируемое благоустройство
Выполненное и планируемое благоустройство Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства
Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства Чудесные превращения воды в природе (3 класс)
Чудесные превращения воды в природе (3 класс) Волга – главный символ нашего края
Волга – главный символ нашего края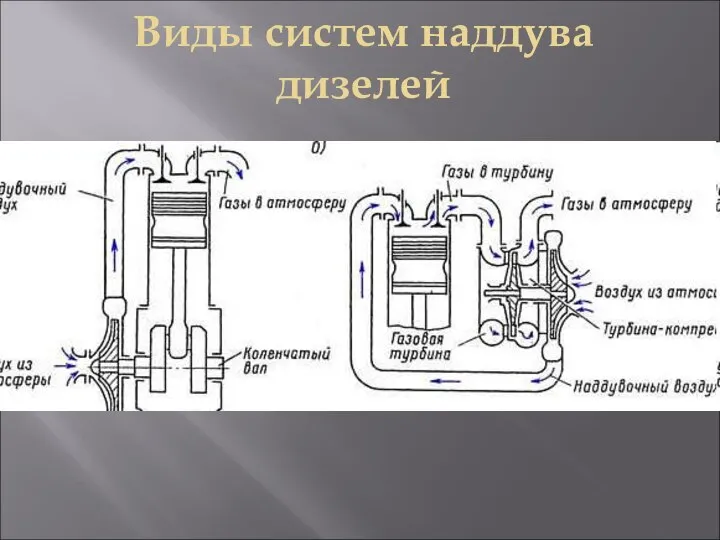 Виды систем наддува дизелей на судне. Аксиально-поршневой насос
Виды систем наддува дизелей на судне. Аксиально-поршневой насос Гражданское общество. Задания для выполнения
Гражданское общество. Задания для выполнения Природные и экологические опасности
Природные и экологические опасности London
London  Семейное право
Семейное право Morphonologie der Verben IPrasens
Morphonologie der Verben IPrasens Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч
Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч Мотивация продавцов-промоутеров SEB
Мотивация продавцов-промоутеров SEB Выражение характера человека в изображении. Женский образ русских сказок
Выражение характера человека в изображении. Женский образ русских сказок Портфолио
Портфолио Школьный музей "Родные истоки"
Школьный музей "Родные истоки" Тип, имя и значение переменной
Тип, имя и значение переменной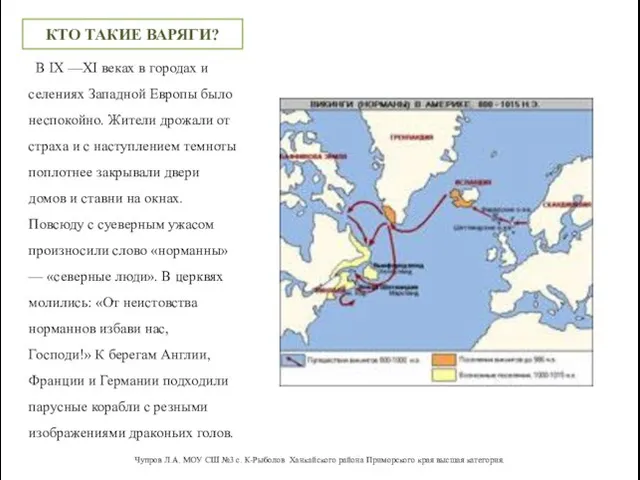 Путь из Варяг в Греки
Путь из Варяг в Греки Масштабируемое решениеот ЛПУ до региона
Масштабируемое решениеот ЛПУ до региона Агроэкосистеемы, или аграрные экологические системы
Агроэкосистеемы, или аграрные экологические системы Религия как одна из форм культуры
Религия как одна из форм культуры Угольная кислота
Угольная кислота