Математика в архитектуре и живописи

Золотое сечение
Деление отрезка в золотом сечении означает, что длина меньшей части относится к длине большей части так же, как длина большей части относится к длине всего отрезка.
A
B
C
φ≈0,62 Ф=1/φ ≈ 1,618
Ряд золотого сечения является геометрической прогрессией
Свойство ряда золотого сечения
Золотые фигуры
Золотыми фигурами называются такие фигуры, стороны которых находятся в золотом соотношении
M
N
P
Q
Золотой прямоугольник
MN:NP=φ
A
B
C
Золотой треугольник
BC:AB=φ

Архитектура
«Архитектурные пропорции – это математика зодчества. А математика – это универсальный язык науки, поэтому мы можем сказать, что пропорции – это универсальный язык науки, язык всеобъемлющий и всесильный, как всесильна и всеобъемлюща сама математика»
А.В. Волошинов
«Всё вокруг – геометрия.
Дух геометрического и математического порядка станет властителем архитектурных судеб»
Ле Корбюзье

Парфенон
Парфенон – одно из самых великих сооружений мира. Храм был возведён при Перикле в Vв. до н.э. Иктином и Калликратом.
Он был построен в дорическом ордере. Снаружи его украсили сценами жестоких битв. На западном фронтоне Парфенона был изображён миф о споре Афины и Посейдона. На главном (восточном) – рождение Афины

Пропорции Парфенона
Современные архитекторы утверждают, что в основе Парфенона лежит золотое сечение.
Жолтовский писал, что высоты поддерживающих (ВС) и поддерживаемых (АC) частей фасада соотносятся в золотой пропорции.
AC:BC=φ
Хэмбидж разбил фасад Парфенона на квадраты и прямоугольники, стороны которых относятся, как 1 к √5.
Легко видеть, что главные вертикальные размеры храма соотносятся в золотой пропорции (см. рисунок)
Золотая пропорция на фасаде Парфенона

Линейчатые поверхности
Линейчатыми называются поверхности, образованные движением прямой в пространстве.
К ним относятся конус и цилиндр.
Цилиндрические своды сооружали в Древнем Риме. Позже математики открыли ещё 2 вида линейчатых поверхностей: гиперболический параболоид и однополостный гиперболоид. Они образованы двумя семействами прямых в пространстве

Однополостный гиперболоид
На основе однополостных гиперболоидов была построена Шаболовская радиобашня
Гиперболический параболоид
Возможности гиперболических параболоидов открыл испанский архитектор Феликс Кандела. Он показал их свойства на самых разных сооружениях – от промышленных зданий до ресторанов и клубов.
На фото изображён вечерний зал в Акапулько.

Собор Парижской Богоматери
Собор Парижской богоматери – один из величайших памятников архитектуры ранней готики.
Огюст Шуази показал, что в основе пропорций фасада собора лежит квадрат, а высота башен равна радиусу окружности, вписанной в этот квадрат
Также на главном фасаде присутствует золотое сечение.

Храм Василия Блаженного
Церковь Покрова на Нерли
Несмотря на простоту форм и лаконичность украшений, храм Покрова на Нерли считается одной из самых красивых церквей России.
В основе храма лежит золотое сечение
Ряд золотого сечения:

Золотое сечение на картине Боттичелли «Рождение Венеры»
Отношение длины картины к её ширине равно φ. Расстояние от левого края картины до головы богини ветра и расстояние от её головы до правого края картины находятся в золотом соотношении, как и расстояние от левого края до руки нимфы и от руки до правого края.
На рисунке показано, что колени делят тело, пупок – туловище, брови – лицо в золотом сечении.

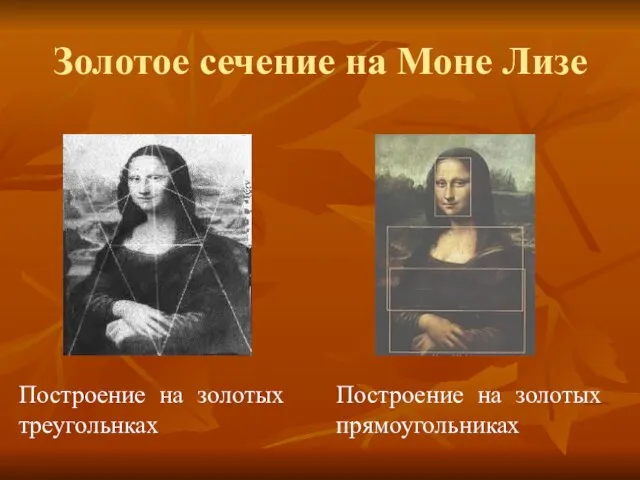
Золотое сечение на Моне Лизе
Построение на золотых треугольнках
Построение на золотых прямоугольниках

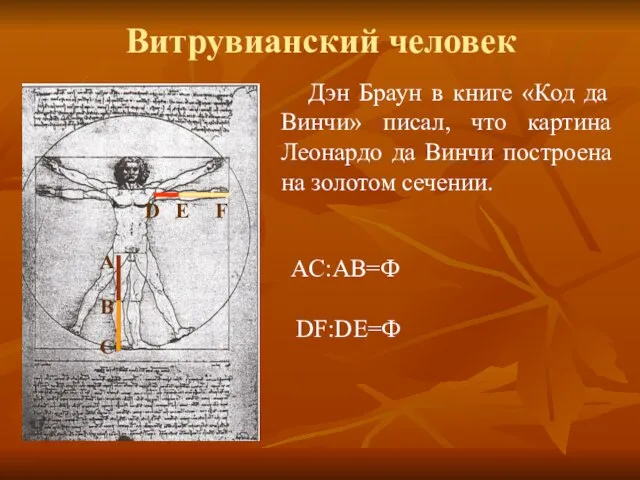
Витрувианский человек
Дэн Браун в книге «Код да Винчи» писал, что картина Леонардо да Винчи построена на золотом сечении.
A
B
C
D
E
F
AC:AB=Ф
DF:DE=Ф

Математическая живопись
Наиболее распространенными темами в математической живописи являются: фракталы, тесселляции, невозможные фигуры и искажённые перспективы.
Иштван Орос «Перекрёстки»
Невозможные фигуры

Искажённые перспективы
Дик Термес «Клетка для человека»

Фракталы
Роберт Фатауэр «Композиция кругов»

Тесселляции
Роберт Фатауэр "Фрактальные рыбы "
Если присмотреться, то можно увидеть, что волна является фрактальной тесселяцией, которая состоит из рыб разных размеров