Тригонометрические функции угла

Что такое косинус угла ?
Это число, которое можно определить следующим образом:
Харьковский В.З.

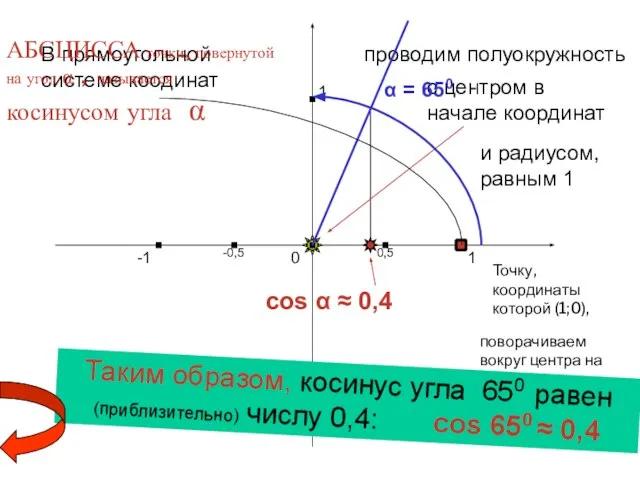
cos α ≈ 0,4
1
0
-1
1
-1
В прямоугольной системе коодинат
проводим полуокружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
АБСЦИССА точки, повернутой на угол α , называется косинусом угла α
α = 650
0,5
-0,5
Таким образом, косинус угла 650 равен (приблизительно) числу 0,4: cos 650 ≈ 0,4
Харьковский В.З.

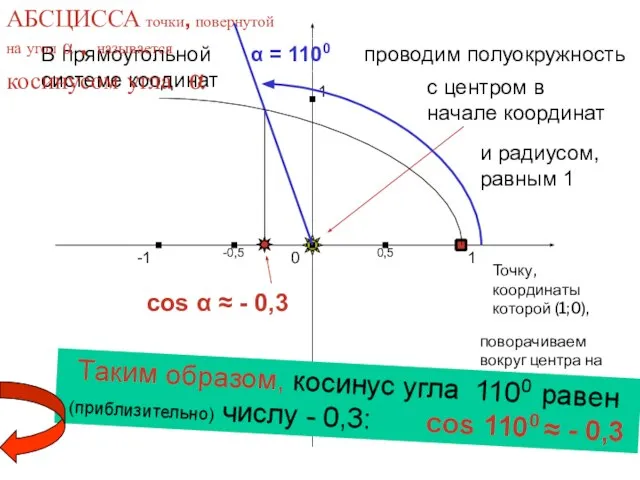
Попробуйте теперь сами:
выполните чертеж и определите (приближенно)
косинус угла 1100
Харьковский В.З.

cos α ≈ - 0,3
1
0
-1
1
-1
В прямоугольной системе коодинат
проводим полуокружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
АБСЦИССА точки, повернутой на угол α , называется косинусом угла α
α = 1100
0,5
-0,5
Таким образом, косинус угла 1100 равен (приблизительно) числу - 0,3: cos 1100 ≈ - 0,3
Харьковский В.З.

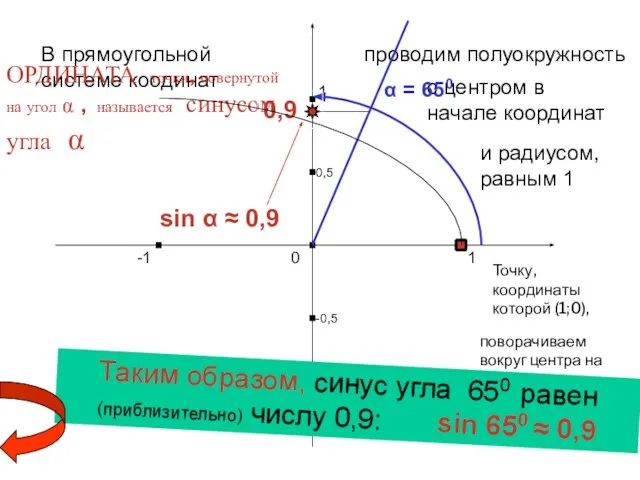
Что такое синус угла ?
Это число, которое можно определить следующим образом:
Харьковский В.З.

1
0
-1
1
-1
В прямоугольной системе коодинат
проводим полуокружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
ОРДИНАТА точки, повернутой на угол α , называется синусом угла α
α = 650
0,5
-0,5
Таким образом, синус угла 650 равен (приблизительно) числу 0,9: sin 650 ≈ 0,9
sin α ≈ 0,9
0,9
Харьковский В.З.

Помните:
синус угла – это ордината точки;
косинус угла – это абсцисса точки
Харьковский В.З.

Найдите самостоятельно
синус другого угла, например
синус угла 1570
Харьковский В.З.

1
0
-1
1
-1
В прямоугольной системе коодинат
проводим полуокружность
с центром в начале координат
и радиусом, равным 1
Точку, координаты которой (1;0),
поворачиваем вокруг центра на угол α
ОРДИНАТА точки, повернутой на угол α , называется синусом угла α
α = 1570
0,5
-0,5
Таким образом, синус угла 1570 равен (приблизительно) числу 0,45: sin 1570 ≈ 0,45
sin α ≈ 0,45
0,45
Харьковский В.З.

Что такое тангенс угла ?
Это число, которое можно определить следующим образом:
tg α =
sin α
cos α
Харьковский В.З.

Что такое котангенс угла ?
Это число, которое можно определить следующим образом:
сtg α =
cos α
sin α
Харьковский В.З.

А теперь задания:
1. Определите:
cos 900
sin 900
sin 1800
cos 1800
tg 1800
cos 450
sin 300
tg 600
ctg 450
2. Сравните :
cos 230 и cos 380
sin 1360 и sin 1380
cos 1170 и cos 1190
tg 30 и ctg 960
sin 890 и cos 00
sin 150 и cos 1650
cos 710 и -cos 1090
Харьковский В.З.

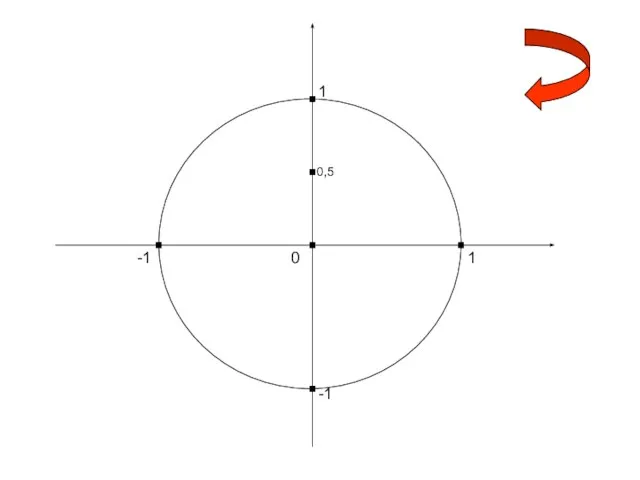
1
0
-1
1
-1
0,5
Харьковский В.З.