Слайд 2Где и как зародилась математика в древних странах
Цель работы:

Слайд 4Иероглифическая запись числа 35736

Слайд 5Разложение
Чтобы правильно подобрать кратное число нужно было знать следующую таблицу значений:
1

x 2 = 2
2 x 2 = 4
4 x 2 = 8
8 x 2 = 16
16 x 2 = 32
Слайд 6Пример разложения числа 25:
Кратный множитель для числа «25» - это 16.
25 –

16 = 9,
Кратный множитель для числа «9» - это 8,
9 – 8 = 1,
Кратный множитель для числа «1» - это 1,
1 – 1 = 0
Таким образом «25» - это сумма трех слагаемых: 16, 8 и 1
Слайд 7Пример
Умножим «13» на «238»:
Известно, что 13 = 8 + 4 +

1. Каждое из этих слагаемых нужно умножить на 238
1 х 238= 238
4 х 238= 952
8 х 238= 1904
238+952+1904=3094
13 х 238= 3094
. Получаем: 13 × 238 = (8 + 4 + 1) × 238 = 8 x 238 + 4 × 238 + 1 × 238 = 3094.
Слайд 13 Римские цифры
Обозначение:
1 I
5 V
10 X
50 L
100C
500D
1000M
Для закрепления в памяти буквенных обозначений цифр в порядке убывания

существует мнемоническое правило:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх.
Соответственно M, D, C, L, X, V, I
Слайд 14Примеры цифр:
0 -
4 IV
8 VIII
9 IX
31 XXXI
46 XLVI
99 XCIX
666 DCLXVI
888 DCCCLXXXVIII
1668 MDCLXVIII
1989 MCMLXXXIX
2009 MMIX
3999 MMMCMXCIX

Слайд 15сокращённый способ для записи больших чисел, таких как 95
95. Сто (C), вычтем

5 (V), получим 95 (VC) вместо XCV
1950: Tысяча (M), вычтем 50 (L), получим 950 (LM). Следствие: 1950 — MLM вместо MCML
Слайд 16Повсеместно записывать число «четыре» как «IV» стали только в XIX веке, до

этого наиболее часто употреблялась запись «IIII». Однако запись «IV» можно встретить уже в документах манускрипта «Forme of Cury», датируемых 1390 годом. На циферблатах часов в большинстве случаев традиционно используется «IIII» вместо «IV»[1], главным образом, по эстетическим соображениям: такое написание обеспечивает визуальную симметрию с цифрами «VIII» на противоположной стороне, а перевёрнутую «IV» прочесть труднее, чем «IIII».






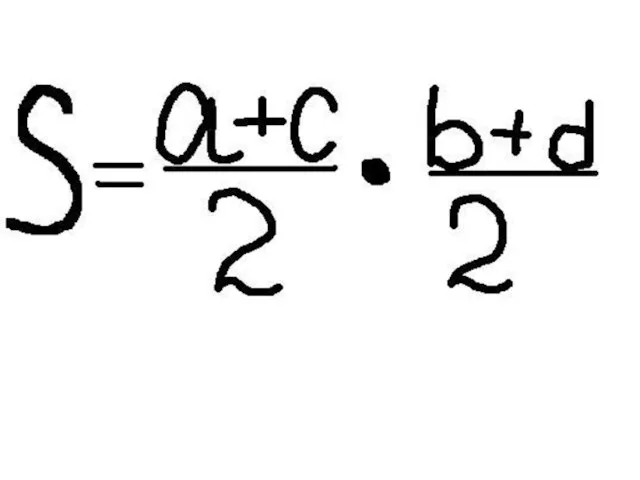
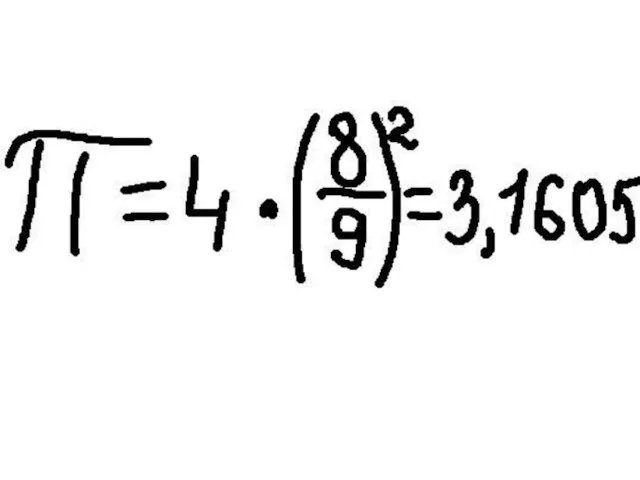
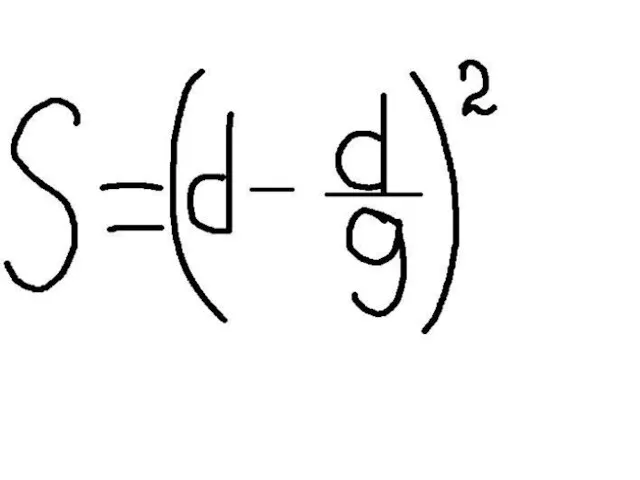
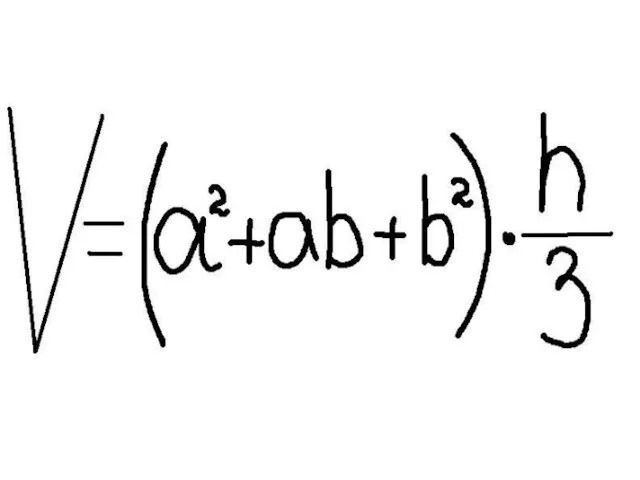






 Закрытое клубное мероприятие для проектных институтов, г. Белгород бизнес-отель Континенталь
Закрытое клубное мероприятие для проектных институтов, г. Белгород бизнес-отель Континенталь Моя будущая профессия. Экономист
Моя будущая профессия. Экономист 9 Технические средства
9 Технические средства ПРОГРАММА СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ СВЕРДЛОВСКОЙ ОБЛАСТИ НА 2011 - 2015 ГОДЫ
ПРОГРАММА СОЦИАЛЬНО-ЭКОНОМИЧЕСКОГО РАЗВИТИЯ СВЕРДЛОВСКОЙ ОБЛАСТИ НА 2011 - 2015 ГОДЫ Примеры задач по геологии 2016
Примеры задач по геологии 2016 Модель процессора
Модель процессора  Наталья и Аксинья - жизненные типы русских женщин в романе "Тихий Дон"
Наталья и Аксинья - жизненные типы русских женщин в романе "Тихий Дон" Рынок
Рынок Организация расследования изготовления и сбыта поддельных официальных денежных единиц Республики Беларусь
Организация расследования изготовления и сбыта поддельных официальных денежных единиц Республики Беларусь Япония в 19 веке
Япония в 19 веке Провода и кабели
Провода и кабели Электронные физминутки для глаз
Электронные физминутки для глаз Powołanie uczniów
Powołanie uczniów Товароведение и экспертиза однородных групп товаров (Раздел: кожевенно-обувные товары)ПродолжениеТема 6. Ассортимент кожаной обу
Товароведение и экспертиза однородных групп товаров (Раздел: кожевенно-обувные товары)ПродолжениеТема 6. Ассортимент кожаной обу Видеоконференция-шаг за шагом
Видеоконференция-шаг за шагом Влияет ли тип темперамента личности на успешность подготовки к ЕГЭ?
Влияет ли тип темперамента личности на успешность подготовки к ЕГЭ? Past simple, теория и вопросы,задания
Past simple, теория и вопросы,задания Черты российской системы организации маркетинговой деятельности
Черты российской системы организации маркетинговой деятельности 439002689
439002689 Опыт ТПУ в разработке и эксплуатации виртуальных лабораторных работ и компьютерных тренажёров
Опыт ТПУ в разработке и эксплуатации виртуальных лабораторных работ и компьютерных тренажёров Презентация на тему дыхание и здоровье человека
Презентация на тему дыхание и здоровье человека Премьера короткометражного художественного фильма Vонетка
Премьера короткометражного художественного фильма Vонетка Город сквозь времена и страны. Образно-стилевой язык архитектуры прошлого
Город сквозь времена и страны. Образно-стилевой язык архитектуры прошлого Р Е К Л А М Н О Е А Г Е Н Т С Т В О
Р Е К Л А М Н О Е А Г Е Н Т С Т В О Стратегии роста
Стратегии роста Тропинка к своему я. Уроки психологии в начальной школе
Тропинка к своему я. Уроки психологии в начальной школе Приветствия разных стран мира
Приветствия разных стран мира АРМ "Метрoлог" версии 5.0
АРМ "Метрoлог" версии 5.0