Международная научно-практическая конференцияОБРАЗОВАТЕЛЬНЫЕ ТЕХНОЛОГИИ XXI века:информационная культура и медиаобразование О

Мультимедиа технологии
в проектной деятельности учащихся
Милешина Ольга Ивановна
учитель информатики и ИКТ
ГБОУ СОШ №546 г. Москвы

Проектная деятельность

Ежегодная школьная
научно-практическая конференция
Познать непознанное сложно!
Преодолев и лень и слабость,
Увидеть в капле море можно,
Чтоб испытать успех и радость!

Участники школьной конференции 2011-2012 уч.год

О проекте
школьная пресса
Формирование собственной системы восприятия и обработки информации
- развитие критического мышления и аналитических способностей школьников;
- становление творческой позиции личности, развитие навыков общения через коммуникацию;
Формирование этико-эстетической информационной среды общения
-освоение информации через практическую деятельность;
Открытость ко всему новому и неизведанному-
одно из лучших качеств человека. Именно это помогает исследовать мир юным первооткрывателем, и, конечно же, журналистам

Работу выполнили Шарипова Эльвира, Юрченко Валерия
Ученицы 9 класса «В» ГБОУ СОШ №546 г. Москва
Руководитель: Милешина Ольга Ивановна
Учитель информатики и ИКТ ГБОУ СОШ №546 г. Москва

Цель проекта:
Освещение школьной жизни
PR школы
Демонстрация технических возможностей новых информационных технологий в образовании
Раскрытие творческих навыков учащихся

«ПреСск@» - ежемесячная газета
ГБОУ СОШ №546

Ольга Ивановна
Милешина
Учитель
Информатики и ИКТ
ГБОУ СОШ № 546
Руководитель
Проекта
Эльвира
Шарипова
Ученица 9 «В»
ГБОУ СОШ №546
Главный редактор
Дизайнер
Верстальщик
Редакторы:
Валерия
Юрченко (9 «В»)
Валерия Морозова
(9 «Б»)
Екатерина
Коломиец
(Выпускница)
Полина
Рачковская (9 «Б»)

Интервьюеры:
Анастасия
Филиппова
(10 «А»)
Татьяна
Захарова (10 «А»)
Анна
Максименко
(11 «А»)
Фотокорреспонденты:
Мария
Шашкова
(9 «Б»)
Полина
Черноус (11 «А»)
Сергей Степанян
(11 «А»)
Екатерина
Коровкина (11 «А»)

Постоянные рубрики газеты:

Титульные страницы

Содержание

Статьи

ПЕРЕМЕНКА

Редколлегия

Программы
(язык программирования TurboPascalABC),
написанные для изображения отдельных кривых, наглядно показывают процесс моделирования вида кривой, в зависимости от параметров
входящих в её уравнение.
Мультимедиа технологии в программировании

ПРОГРАММИРОВАНИЕ КРИВЫХ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ
Выполнил: Шатунов Алексей
учащийся 9 «В» кл.
Руководитель: Милешина О.И.
учитель информатики и ИКТ
ГБОУ СОШ №546
Москва 2012

Развитие цифровой графики обязано классической математике и ее законам, формулам и закономерностям. В природе много красивого, но оказывается, что все, что мы видим, имеет математическую природу.

Содержание:
Кривые в технике и природе
Полярная система координат
Программирование кривых в полярной системе координат:
Полярная роза
Кардиоида
Спираль Архимеда
Лемниската Бернулли
Улитка Паскаля

Цель: рассмотреть некоторые кривые в полярной системе координат и показать, как можно использовать компьютер для их изучения.
Задачи:
Рассмотреть графики некоторых замечательных кривых известных математиков в полярной системе координат.
Написать программы на PascalABC для наглядного представления кривых и изучения их свойств.
Рассмотреть наличие кривых в природе, технике.

Кривые в технике и природе

Полярная система координат
Полярная система координат - двумерная система координат, в которой каждая точка на плоскости определяется двумя числами - полярным углом и полярным радиусом.
Каждая точка в полярной системе координат может быть определена двумя полярными координатами, что обычно называются r (радиальная координата) и φ (угловая координата. Координата r соответствует расстоянию до полюса, а координата φ равна углу в направлении против часовой стрелки от луча через 0°.

Кривые в полярной системе координат:
Полярная роза (роза Гранди)
Полярная роза - плоская кривая, напоминающее символическое изображение цветка. Данная кривая описывается уравнением в полярной системе координат в виде
Здесь a и k - постоянные, определяющие размер (a) и количество лепестков (k) данной розы.

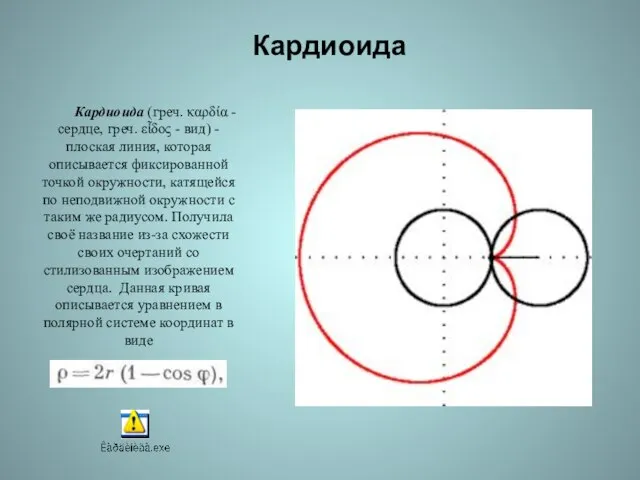
Кардиоида
Кардиоида (греч. καρδία - сердце, греч. εἶδος - вид) - плоская линия, которая описывается фиксированной точкой окружности, катящейся по неподвижной окружности с таким же радиусом. Получила своё название из-за схожести своих очертаний со стилизованным изображением сердца. Данная кривая описывается уравнением в полярной системе координат в виде

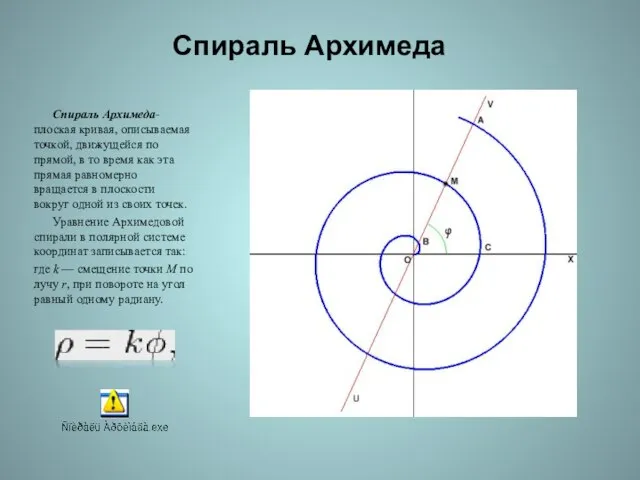
Спираль Архимеда
Спираль Архимеда- плоская кривая, описываемая точкой, движущейся по прямой, в то время как эта прямая равномерно вращается в плоскости вокруг одной из своих точек.
Уравнение Архимедовой спирали в полярной системе координат записывается так:
где k — смещение точки M по лучу r, при повороте на угол равный одному радиану.

Лемниската Бернулли
Лемниската Бернулли - плоская алгебраическая кривая. Определяется как геометрическое место точек, произведение расстояний от которых до двух заданных точек (фокусов) постоянно и равно квадрату половины расстояния между фокусами.
В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Эту лемнискату называют в честь швейцарского математика Якоба Бернулли, положившего начало её изучению.

Улитка Паскаля
Улитка Паскаля- плоская кривая, множество точек М и М’, расположенных на прямых, исходящих из одной точки О данной окружности, на одинаковом расстоянии по обе стороны от точки Р пересечения прямых с окружностью.

Результаты исследования
В процессе работы над темой
мы изучили переход от декартовой системы координат к полярной и обратно;
познакомились с отдельными главами высшей математики (аналитической геометрии) изучающей плоские кривые;
создали программы, изображающие отдельные кривые;
исследовали изменения вида кривой, в зависимости от параметров входящих в её уравнение;
познакомились с некоторыми замечательными кривыми известных – математиков.

Источники информации:
Практика программирования, Ю. Кетков, А. Кетков, СПб, Петербург, 2006г.
Turbo Pascal. С. А. Немнюгин.- СПб: Издательство «Питер», 2007.-496 с.:ил.
Turbo Pascal: учитесь программировать, О. А. Меженный, Москва:
изд. дом «Вильямс», 2009г
Эйджел Й. Практическое введение в машинную графику. М.: Радио и связь, 2008. - 136 с.
ru.wikipedia.org/wiki/

Программирование фракталов в Turbo Pascal 7
Выполнил: Михнушев Анатолий
учащийся 9”В” класса
Руководитель: Милешина Ольга Ивановна,
учитель информатики и ИКТ
ГОУ СОШ №546 ЮАО
Москва 2011

Фрактал - геометрическая фигура, состоящая из частей, которые могут быть поделены на части, каждая из которых будет представлять уменьшенную копию целого.
Fractal от латинского слова fractus, означает разбитый (поделенный на части).
Основное свойство фракталов: самоподобие, в самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.
ПОНЯТИЕ
ФРАКТАЛА

Фракталы в природе

Фракталы в природе
Природа зачастую создаёт удивительные и прекрасные фракталы, с идеальной геометрией и такой гармонией, что просто замираешь от восхищения.
От гигантских гор, до того, что мы кушаем за обедом, везде можно увидеть идеальную гармонию
Морские раковины
Nautilus является одним из наиболее известных примеров фрактала в природе
Молнии
Молнии ужасают и пугают и одновременно восхищают своей красотой. Фракталы созданные молнией не произвольны и не регулярны

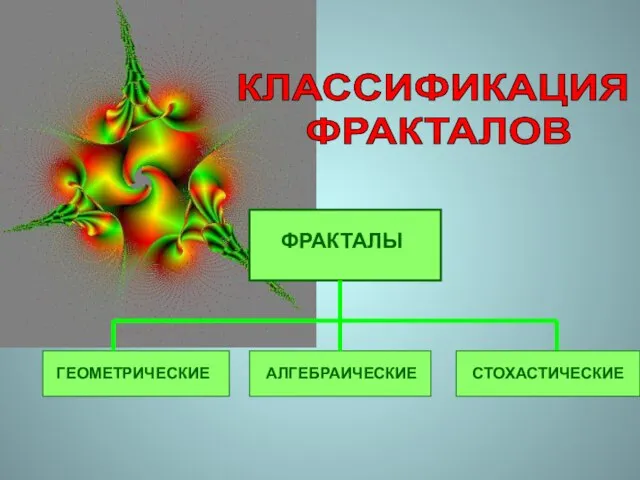
КЛАССИФИКАЦИЯ
ФРАКТАЛОВ
ГЕОМЕТРИЧЕСКИЕ

Это «функции - монстры», которых так называли за недифференцируемость в каждой точке.
Геометрические фракталы являются также самыми наглядными, т.к. сразу видна самоподобность.
Для построения геометрических фракталов характерно задание «основы» и «фрагмента», повторяющегося при каждом уменьшении масштаба.
ГЕОМЕТРИЧЕСКИЕ ФРАКТАЛЫ

Треугольник
Серпинского

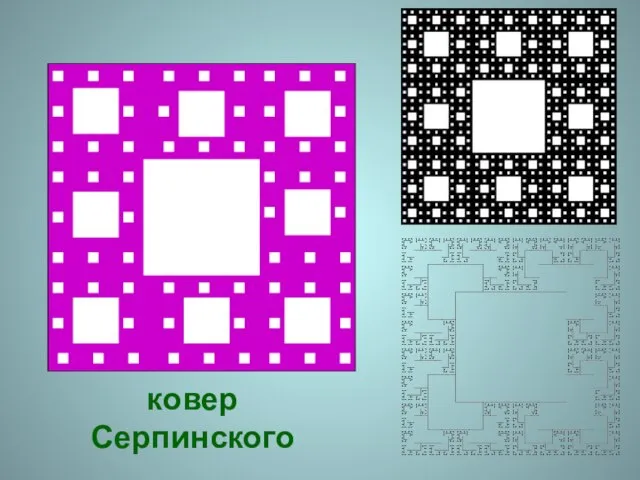
ковер Серпинского

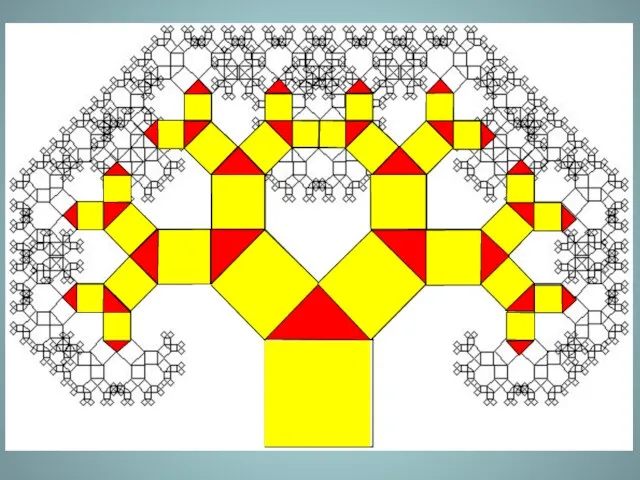
Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты.
В наш век эта фигура Пифагора выросла в целое дерево.
Впервые дерево Пифагора построил А.Е. Босман (1891-1961) во время Второй Мировой войны, используя обычную чертежную линейку.
Дерево Пифагора

Это фракталы, которые можно построить, используя простые алгебраические формулы.
Получают их с помощью нелинейных процессов в n–мерных пространствах.
Самыми известными из них являются множества Мандельброта и Жюлиа, Бассейны Ньютона
АЛГЕБРАИЧЕСКИЕ ФРАКТАЛЫ

Это фракталы, при построении которых в итеративной системе случайным образом изменяются какие-либо параметры.
Эти фракталы используются при моделировании рельефов местности и поверхности морей, процесса электролиза.
Стохастические фракталы очень похожи на природные объекты – несимметричные деревья, изрезанные береговые линии.
СТОХАСТИЧЕСКИЕ ФРАКТАЛЫ

Источники информации:
Мандельброт Б. Фрактальная геометрия природы. – М.: «Институт компьютерных исследований», 2002.
Данилов Ю.А., Красота фракталов, Московский Международный Синергетический Форум.
Шабаршин А.А., Введение во фракталы. 1998. Екатеринбург.

Результаты
Окружной конкурс творческих работ по компьютерным технологиям
2011-2012 уч. год
Номинация «Программирование» Шатунов А. - I место.
Номинация «Газета»
Шарипова Э., Юрченко В.- I место.
Номинация «Анимация»
Нестеров А. – II место
Угаров В. - III место.

Международный образовательный проект
Медиафестиваль для школьников
декабрь 2011г. - февраль 2012г.
Здоровый образ жизни, я против курения - Угаров Виталий, 7А класс, школа №546, г.Москва, руководитель - Милешина О.И., учитель информатики и ИКТ ГБОУ СОШ №546
Великий день Бородина - Гусаков Александр, Пыльцин Глеб, 9В класс, школа №546, г.Москва, руководитель - Милешина О.И., учитель информатики и ИКТ ГБОУ СОШ №546
Софизмы - Олег Яковлев, 8В класс, школа №546, г.Москва, руководители - Милешина О.И., учитель информатики и ИКТ, Рудюк И.Л. учитель математики ГБОУ СОШ №546
И помнит мир спасенный - Скворцова Наталья, 11А класс, школа №546, г.Москва, руководитель - Милешина О.И., учитель информатики и ИКТ ГБОУ СОШ №546
Школьная газета "ПреСск@" - Шарипова Э., Юрченко В., Морозова В., Рачковская П., Шашкова М., 9 класс, школа №546, г.Москва, руководитель - Милешина О.И., учитель информатики и ИКТ ГБОУ СОШ №546