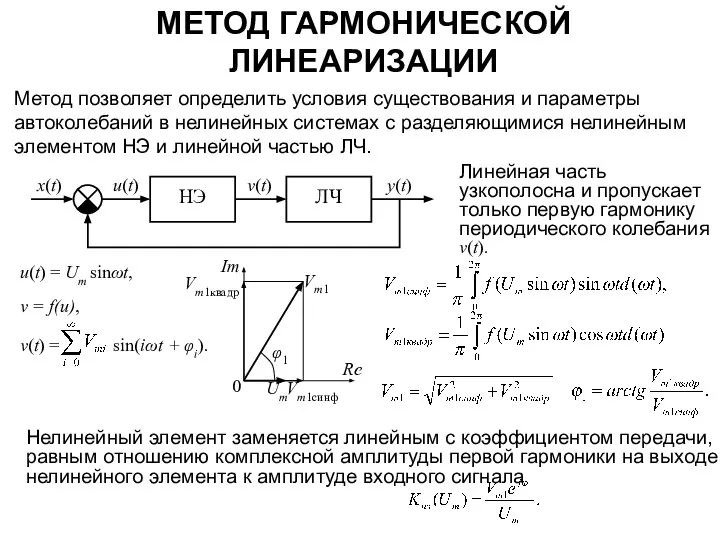
Метод гармонической линеаризации. Метод статистической линеаризации. Лекция 12

МЕТОД ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
Нелинейный элемент заменяется линейным с коэффициентом передачи, равным отношению комплексной амплитуды первой гармоники на выходе нелинейного элемента к амплитуде входного сигнала
Метод позволяет определить условия существования и параметры автоколебаний в нелинейных системах с разделяющимися нелинейным элементом НЭ и линейной частью ЛЧ.
Линейная часть узкополосна и пропускает только первую гармонику периодического колебания v(t).
v(t) = sin(iωt + φi).
Vm1синф
Vm1квадр
u(t) = Um sinωt,
v = f(u),

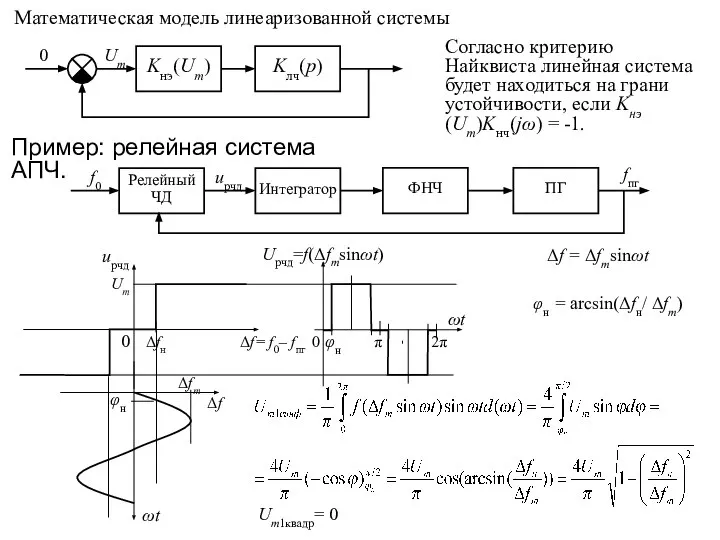
Математическая модель линеаризованной системы
Пример: релейная система АПЧ.
Согласно критерию Найквиста линейная система будет находиться на грани устойчивости, если Kнэ(Um)Kнч(jω) = -1.
Um1квадр= 0
Δf = Δfmsinωt
φн = arcsin(Δfн/ Δfm)

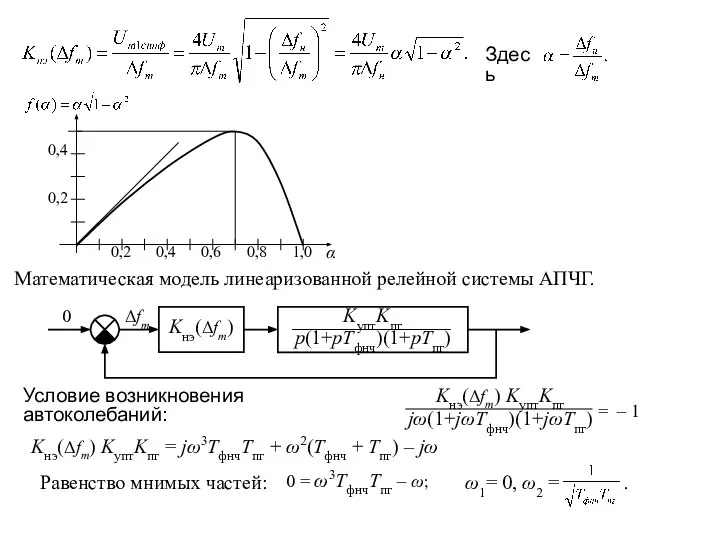
0,4
0,2
0,6
0,8
1,0
α
0,2
0,4
Математическая модель линеаризованной релейной системы АПЧГ.
Условие возникновения автоколебаний:
Kнэ(Δfm) KуптKпг = jω3TфнчTпг + ω2(Tфнч + Tпг) – jω
Равенство мнимых частей:
ω1= 0, ω2 = .
0 = ω3TфнчTпг – ω;

Равенство вещественных частей:
Kнэ(Δfm)KуптKпг = ω2(Tфнч + Tпг),
0,4
0,2
0,6
0,8
1,0
α
0,2
0,4
При С = С1 решения уравнения не существует и автоколебания в системе невозможны.
При С > 0,5 устанавливается режим работы без автоколебаний.
При С = С2 существует два решения уравнения: α1 и α2. Одно из них (α1) соответствует устойчивому режиму работы, другое (α2) – неустойчивому.
Амплитуда автоколебаний определится из выражения α = α1: Δfm= Δfн/ α1.

МЕТОД СТАТИСТИЧЕСКОЙ ЛИНЕАРИЗАЦИИ
Случайный процесс представляется в виде суммы математического ожидания и центрированного случайного процесса.
u(t) = mu + ů(t)
v = f(u)
1)
1) равенство математических ожиданий и дисперсий процессов v(t) и z(t),
2) минимум среднеквадратического отклонения процессов v(t) и z(t).
K(p)
Критерии эквивалентности замены нелинейного элемента линейным:
mv = mz = K0mu.

2)
Минимум σ2 по K0:
2K0mu2 – 2mvmu = 0
Минимум σ2 по K1: